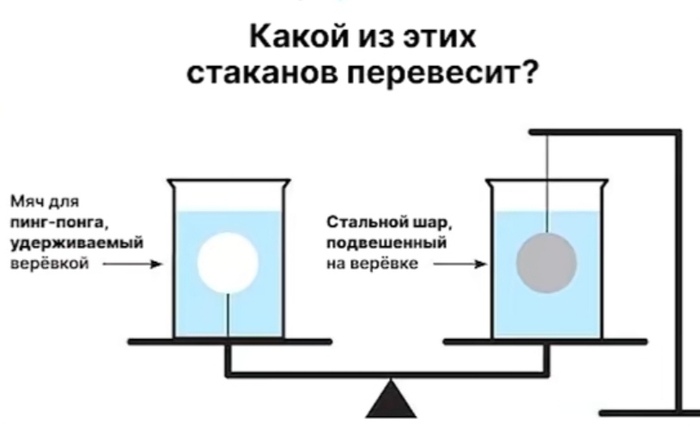
Солевой эксперимент #25: Финишная прямая
Всем привет!


Банки перед заменой


Всё, что осталось
Как вы заметили, сегодня с помощником, так что проведём последние замеры.


1.1 г/мл и 6060 ppm*


1.05 г/мл и 5390 ppm*
* Parrots Per Monkey


После замены
Собственно, Мозырь всё. В Славяночке, похоже остался один песок, увидим через неделю.
На сегодня всё, следующий раз будет последним. Итоги будут отдельным постом. До встречи через неделю и всем добра!
"Математика - поиск истины" Морис Клайн / Пересказ основных идей / Cтр. 200-298
Пересказ основных идей книги "Математика - поиск истины" Мориса Клайна
Содержание
--- Фрагмент 1 ---
Как Эйнштейн заменил гравитацию геометрией
Что если тяжесть вовсе не сила, а «яма» в пространстве? Эйнштейн предложил именно такую картину: всякая масса будто проваливается в четырёхмерный матрас пространства-времени и заставляет рядом находящиеся тела катиться к ней по кратчайшим линиям – геодезическим.
Простая аналогия: шарик на растянутом полотне. Он делает впадину, и второй шарик, пущенный рядом, закручивается по спирали, словно его «тянет» первый. На деле никакой притягивающей силы нет – есть только искривлённая поверхность.
Зачем понадобилось такое объяснение?..
--- Фрагмент 2 ---
Как Эйнштейн изменил наш взгляд на мир: от света до времени
Что сделал Эйнштейн для нашего понимания мира
Альберт Эйнштейн предсказал два удивительных явления, которые потом подтвердили наблюдения. Во-первых, он сказал, что свет от далёких звёзд будет отклоняться, когда пройдёт мимо Солнца. Во-вторых, он объяснил, почему свет от звёзд меняет свой цвет, становясь более красным. Эти открытия стали важным подтверждением его теории относительности.
Почему трудно поверить в теорию относительности...
--- Фрагмент 3 ---
Как мы придумали себе «вещи», которые не существуют по-настоящему
Введение
Мы привыкли думать, что пространство, время и вещи вокруг нас живут «сами по себе». Оказывается, это удобная выдумка, придуманная ещё Аристотелем и подхваченная Ньютоном. Мы сами разрезали мир на удобные кусочки и забыли, что делали это «ножницами» своего мозга.
От геометрии до «исчезновения» материи...
--- Фрагмент 4 ---
Как учёные разбирались, из чего состоит материя
Сначала все верили, что атом — это последний мелкий «кирпичик», который нельзя разделить. В XVII веке Роберт Бойль положил начало химии, а в 1808 году Джон Дальтон добавил: каждый элемент — это свой сорт таких неделимых шариков. Вещество, например вода, получается, когда шарики разных сортов сцепляются в молекулы.
Половина XIX века: известно уже шесть десятков «сортов» атомов. Дмитрий Менделеев расставил их по весу и заметил закономерность: свойства повторяются через каждые семь элементов. Чтобы картинка не рвалась, он оставил в таблице пустые клетки и предсказал: «Там будут новые элементы». Через годы нашлись скандий, галлий и германий — всё точь-в-точь как он описал. Номера в его таблице (1 — водород, 2 — гелий и далее до 103-го лоуренсия) до сих пор используются.
Однако «неделимость» продержалась недолго. В 1897 году Джозеф Томсон вытащил из атома лёгкие отрицательные частицы — электроны. Получилась модель «пудинг с изюминками»: плюсовая «каша» с вкраплёнными минусовыми «изюминками». Почти вся масса сидела в центре. В 1911 году Эрнест Резерфорд уточнил: внутри атома есть крошечное, тяжёлое, плюсовое ядро, вокруг него летают электроны, как планеты вокруг Солнца. Чтобы закрыть «лишний» вес, он догадался о нейтронах — нейтральных соседях протонов. Атомы одного элемента могут иметь разное число нейтронов; такие «братья» называются изотопами.
--- Фрагмент 5 ---
Как учёные поняли, что электрон — это и волна, и частица, и «облако»
Почему электрон не падает на ядро
Резерфорд сравнил атом с миниатюрной планетной системой: ядро — это Солнце, электроны — планеты. Но по законам физики вращающийся электрон должен терять энергу и воткнуться в ядро за доли секунды. Этого не происходит. Бор решил загадку простым правилом: «Электрон может кататься только по разрешённым круговым дорожкам. Прыгнул на дорожку ближе — выбросил свет, прыгнул дальше — свет проглотил. Между дорожками летать нельзя». Эти прыжки и есть кванты света. Правило работает, но не объясняет, почему именно так.
Частица может быть волной...
--- Фрагмент 6 ---
Как учёные поняли, что атомный мир живёт по законам случая
Сначала казалось: электрон – это просто крошечный шарик. Однако в 1927 году три лаборатории независимо показали: если пустить электроны через кристалл, они образуют картину, как у волн на воде, огибающей столбик причала. Это заставило признать: каждая частица умеет быть и волной, и точкой одновременно.
Появилась неприятная загадка: если электрон «размазан» волной, где тогда его электрический заряд? В 1926 году Макс Борн выход нашёл: волна – это не сама частица, а карта вероятностей. Где волна выше, там 80 % шансов поймать электрон как точку, где ниже – 20 %. Больше никакой «мазни»; есть только ставки на рулетке природы.
Эйнштейн и Планк такому не радовались: «Бог не играет в кости!» – возмущался Эйнштейн. Но природа оказалась упрямее. В 1927 году Вернер Гейзенберг доказал: одновременно точно узнать, где электрон и куда он летит, нельзя. Чтобы увидеть место, нужно подсветить фотоном, но толчок фотона сбивает скорость. Чем точнее одно, тем туманнее другое. Это не недостаток приборов – сама ткань микромира так устроена.
--- Фрагмент 7 ---
Что скрывается внутри атома и почему «кирпичики» материи ведут себя так странно?
1. Частицы умеют исчезать и рождаться заново
Энергия превращается в пару «электрон + позитрон» и наоборот: при встрече эти двое исчезают, превращаясь в свет. То же происходит с другими частицами: если собрать протон и антипротон, они превратятся в лёгкие частицы-мезоны. Из античастиц можно построить антивещество – зеркальную копию обычного.
2. Четыре силы держат мир вместе...
--- Фрагмент 8 ---
Что осталось неизменным в мире, где всё превращается?
Сегодня мы знаем: атомные ядра рождают и уничтожают частицы, а сама Вселенная расширяется. В таком мире исчезла привычная «вещь» — твёрдая, вечная, делимая субстанция. Остались только две величины: масса и энергия, которые переходят друг в друга по формуле E = mc². Пример: в ускорителе энергия пучка превращается в новые частицы, и никакая «материальная крошка» не сохраняется.
Почему мы этого не замечаем дома? Даже пылинка в миллиарды раз тяжелее электрона. Когда масса большая, квантовые эффекты «смазываются» и нам видится привычный мир: стакан, стол, книга. Для микромира же электрон одновременно «размазан» по пространству и ведёт себя как частица. Теория точно предсказывает, где он окажется, но не объясняет, «как он туда попал». Мы пользуемся и волнами, и частицами — удобным математическим рецептом, а не картинкой «как на самом деле».
...
--- Фрагмент 9 ---
Как математика изменила наше представление о реальности
Когда ученые начали использовать математику для описания мира, они сделали неожиданные открытия. Максвелл уравнениями предсказал существование радиоволн, которые мы не можем ни увидеть, ни почувствовать. Но включите радио - и вы их «услышите». Позже Эйнштейн показал, что время и пространство не абсолютны, а зависят от наблюдателя. Это противоречит здравому смыслу, но GPS в вашем телефоне работает именно благодаря этой теории.
Квантовая физика пошла еще дальше. Оказалось, что атомы состоят из частиц, которые ведут себя как волны и не имеют точного положения в пространстве. Представьте, что ваша машина одновременно стоит в гараже и на парковке, пока вы не посмотрите на неё. Причудливо? Но без этого знания не работают компьютерные чипы и лазеры.
Чем глубже мы заглядываем в мир микрочастиц, тем меньше он похож на наш повседневный опыт. Оказывается, не существует «твердой» материи - всё состоит из крошечных частиц, которые постоянно появляются и исчезают. Даже стол, за который вы облокачиваетесь, на самом деле - это «пустое» пространство с редкими вкраплениями энергии.
--- Фрагмент 10 ---
Как мы узнаём, что вокруг нас реально
Раньше считали, что мир существует «сам по себе», и человек может за ним просто понаблюдать, не вмешиваясь. Но когда физики стали изучать атомы и ещё меньшие частицы, выяснилось: наблюдатель и его приборы меняют то, что происходит. Мы не видим сами частицы, а только их «следы» на экранах и фотоплёнках. Поэтому законы физики теперь описывают не «объективный мир», а то, что мы о нём можем узнать.
В квантовой механике вообще нет точных значений: всё выглядит как средняя картина по множеству измерений. Представьте, что вы пытаетесь понять, где сидит мяч, но можете судить только по вмятинам на подушке: мяч сам вы увидеть не можете, а подушка каждый раз пружинит по-новому.
Математика помогает строить модели, но это не значит, что цифры и формулы «сами по себе» правдивы. Иоганн Кеплер подобрал эллипс для орбиты Марса просто потому, что эта кривая была известна и хорошо подходила к грубым измерениям. На самом деле планеты движутся сложнее, но более точные данные появились позже. То же с Эйнштейном: он взял готовую риманову геометрию, потому что она ложилась в уравнения, а не потому что «природа приказала» именно ею пользоваться.
--- Фрагмент 11 ---
Что такое научная истина и можно ли ей доверять
Когда мы меряем длину линейкой, кажется, что всё просто: 10 сантиметров есть 10 сантиметров. Но если линейка нагреется, она станет длиннее, а мы этого даже не заметим. Значит, наши «точные» измерения зависят от погоды в комнате. То же с площадями и объёмами: они тоже «плавают».
Математика не показывает мир таким, каким мы его видим. Она строит удобные «картинки-формулы», которые помогают считать и предсказывать, но не копируют реальность точь-в-точь. До XIX века учёные верили, что у природы есть «правильный» план, и математика его раскрывает. Потом поняли: мы сами придумываем правила игры. Если формула подходит к нескольким явлениям — хорошо, берём её. Почему природа подчиняется? Никто не знает. Землетрясения, метеориты, эпидемии напоминают, что Вселенная не обязана быть удобной для наших формул. Удачная теория — как найти на улице стодолларовую купюру: приятно, но случайно.
Физические законы часто умирают. Сегодняшняя «истина» завтра может оказаться ошибкой. Наши теории — это временные инструкции, а не вечные заповеди. Камни и деревья мы трогаем руками, а вот электроны и кварки — лишь удобные цифры в уравнениях. Считать их «настоящими» почти невозможно.
--- Фрагмент 12 ---
Математика: открываем или изобретаем?
Две большие школы спорят о том, что такое математика.
Первая школа считает: математика ждёт нас где-то «наверху», как неизведанная планета. Мы не придумываем круг или число π – мы их находим, точно так же, как археолог находит древний горшок. Гаусс, Гильберт, Харди говорили: «Теоремы существуют сами по себе, мы лишь записываем то, что увидели».
Вторая школа отвечает: всё, что в математике, родилось в человеческой голове. Числа, аксиомы, теоремы – это наши удобные инструменты, придуманные для решения задач. Дедекинд прямо писал: «Число – это продукт нашего разума, мы – божественная раса, способная творить». Кант, Витгенштейн, интуиционисты добавляют: математика не «лежит» в природе, она строится, как дом, кирпич за кирпичом.
--- Фрагмент 13 ---
Почему математика вообще работает?
Физики давно заметили странную вещь: формулы, выведенные на бумаге, потом обязательно срабатывают в реальности. Электромагнитные волны, атомное ядро, гравитация – всё подчиняется уравнениям, которые человек придумал в голове.
Почему так происходит?
1. Мы берём несколько простых наблюдений (аксиомы) и логически выводим из них сотни следствий. Удивительно, что эти следствия потом подтверждаются опытом.
...
--- Фрагмент 14 ---
Как люди пришли к мысли, что мир устроен по математическим законам
Сначала древние греки просто верили: всё вокруг подчинено геометрии. Потом в Средневековье к этой вере добавили Бога. Люди решили, что Бог создал мир по математическому чертежу, а учёные занимаются тем, что разгадывают этот божественный план. Получалось, что изучать природу — всё равно что читать священную книгу, только вместо букв там числа и формулы.
Рене Декарт усилил эту идею. Он сказал: у человека от рождения в голове есть понятия о пространстве, времени и числах. Наши глаза и уши обманывают нас, а вот математика не врёт. Почему? Потому что добрый Бог не стал бы давать нам разум, который ведёт к заблуждению. Значит, если мы додумались до какой-то математической истины, она обязательно отражает реальный мир.
За Декартом потянулись другие. Галилей заявил, что природа — это книга, написанная математическими буквами. Кто не знает математику, тот блуждает в темноте. Ньютон считал свои формулы доказательством существования Бога и сравнивал его с часовщиком, который запустил механизм мира и следит, чтобы всё работало чётко. Даже Лейбниц, хоть и не распространял математику на всё подряд, всё равно верил, что мир построен на вычислениях.
--- Фрагмент 15 ---
Как математика вытеснила Бога из науки
Сначала учёные видели в математике язык Бога. Лейбниц писал: когда Бог считает, рождается мир. Ньютон, Галилей и другие были уверены: найдя математический закон, они подсматривают замысл Творца. Красота и точность формул казались прямым доказательством божественного разума.
Постепенно внимание сместилось. Сначала восхищались планом создания, потом — самим планом. Лаплас отдал Наполеону книгу о движении планет и спокойно ответил: «Мне не понадобилась гипотеза Бога». Математики всё реже поднимали глаза к небу, всё чаще — опускали их на формулы.
К XVIII веку вера в Бога как в главного математика мира почти исчезла. Дидро требовал: «Покажите мне Бога — тогда поверю». Коши, оставаясь верующим, всё же отделял науку от религии. Математика стала самодостаточной: не нуждалась в божественном авторе, только в точных расчётах.
...
--- Фрагмент 16 ---
Почему математика умеет предсказывать будущее?
Математика перестала быть королевой наук. Её больше не считают хранительницей абсолютной истины: она не открывает, а только помогает искать. Тем удивительнее, что именно она подарила нам GPS, атомные часы и компьютеры. Получается, вымышленные формулы лучше видят реальный мир, чем наши глаза.
Как так выходит? Учёные предлагают три ответа.
Первый – «подгонка». Математик придумывает правила игры, как шахматист, а потом подстраивает их под наблюдения. Не подошла модель – переделали. Критики шутят: это всё равно что утверждать, что розы не вянут, потому что садовник никогда не умирал среди цветов.
--- Фрагмент 17 ---
Почему математика так хорошо описывает мир?
Математика кажется волшебной: человек придумывает формулы, а они потом предсказывают, как ведёт себя Вселенная. Откуда это совпадение?
Учёные спорят об этом уже сто лет. Одни считают, что мы просто придумываем удобные схемы. Пуанкаре показал: если Земля не плоская, а вогнутая, как седло, геометрия Лобачевского будет работать не хуже обычной. Мы выбираем простейшую теорию из множества возможных, как выбираем удобную дорогу домой. Математика тогда похожа на удобную карту, а не на фотографию местности.
Другие уверены: мир сам устроен по математическим законам. Джеймс Джинс писал, что природа «знает» математику, а мы просто открываем её правила. Эрмит шутил: математики не изобретают числа, а находят их, как зоологи новые виды.
--- Фрагмент 18 ---
Что такое математика: точная наука или человеческое изобретение?
Математика — это не абсолютная истина, а удобный инструмент, который люди создали для описания окружающего мира. Как молоток помогает забить гвоздь, так математика помогает понять, как устроена Вселенная.
Мыслители разных эпох пришли к одному выводу: все математические понятия — числа, геометрические фигуры, формулы — родом из повседневного опыта. Мы научились считать, потому что нужно было делить добычу. Мы изобрели геометрию, чтобы измерять землю и строить дома.
Даже великие математики признавали: их теоремы не отличаются от научных гипотез. Бертран Рассел сначала верил, что математика вечна и незыблема, но потом признал: геометрия физического мира — это не чистая логика, а практическое знание, проверенное опытом.
--- Фрагмент 19 ---
Еще о том почему математика так хорошо описывает мир.
Математика — это не открытие, а изобретение человека. Мы сами придумываем числа, формулы и теоремы. Однако удивительно, что эти придуманные вещи потом идеально подходят для описания реального мира — от движения планет до работы компьютера.
Учёные признают: они не могут объяснить, почему это происходит. Французские математики под псевдонимом Бурбаки писали, что связь между математикой и реальностью существует, но никто не знает почему. Физик Эйнштейн называл это главной загадкой мира: как может быть, что Вселенная вообще познаваема?
Современная физика всё больше становится математической наукой. Законы Максвелла об электричестве, уравнения Эйнштейна — всё это прежде всего математические формулы. Даже такие привычные вещи, как гравитация или свет, мы знаем только через уравнения. Мы не видим саму гравитацию — видим только её математическое описание.
--- Фрагмент 20 ---
Как люди придумали, что мир — это часы
Что делает науку с нашими головами
Сначала мы смотрим на природу, потом придумываем формулы, потом снова смотрим и уточняем формулы. Так круг за кругом. Математика в этом процессе работает как переводчик: она соединяет то, что мы видим, с тем, что мы думаем. Получается один большой разговор между человеком и миром.
Почему математика «работает» ...
--- Фрагмент 21 ---
Как учёные пытались объяснить всё простыми шариками и ударами
В начале XVIII века люди верили: природа устроена как огромный бильярд. Бог создал крошечные твёрдые шарики-«кирпичики» — они никогда не ломаются и не стираются. Всё, что мы видим, будто бы сложено из этих шариков. Тепло, свет и даже электричество считались особо тонкими видами такого же вещества: тело греет, потому что «впитывает» тепловую жидкость, как губка воду.
Главное правило было простое: шарик движется, только если его толкнуть. Сила — это толчок. Ньютон добавил толчок под названием «тяготение», чтобы планеты не остановились. Фарадей придумал силовые линии для магнита и электричества. Казалось, что если хорошо поработать, то всё — от звёзд до сердца человека — можно будет записать формулой «толчок → движение».
Французские энциклопедисты даже объявили: «Всё познано, осталось только уточнить цифры». Но уже тому, кто смотрел внимательно, механика казалась тесной. Лейбниц, например, говорил, что внутри каждой крупинки материи скрыта живая «монадка» — маленький моторчик с памятью. А Гельмгольц мечтал свести всё к простым притяжениям и отталкиваниям, но сам же заметил: не всё получается.
...
--- Фрагмент 22 ---
Зачем учёные отказались от «шестерёнок» в природе
Коротко о главном
Физики долго пытались представить, как одно тело толкает другое – словно шестерёнки в часах. Оказалось, математика предсказывает явления лучше, чем любые «механические картинки». Сначала это случилось с тяготением Ньютона, потом с электромагнитными волнами Максвелла, затем с относительностью и квантами. Вместо «как именно толкает» осталось только «по какой формуле считать».
Почему ушли от «механизмов» ...
--- Фрагмент 23 ---
Что такое причина и почему учёные спорят об этом
Когда мы видим, что после события А всегда происходит событие Б, мы автоматически думаем: «А вызвало Б». Но оказывается, это не так очевидно.
Юм: привычка выдаётся за закон
Философ Давид Юм заметил: даже если сто раз наблюдать, как после грома идёт дождь, это не гарантирует, что сто первый раз будет то же самое. Мы просто привыкаем к такой последовательности и начинаем называть гром «причиной» дождя. На самом деле мы не видим самой «связи», видим лишь постоянное соседство во времени.
--- Фрагмент 24 ---
Как мыслили великие: всё предрешено и подсчитано
Декарт, Ньютон и Лаплас верили, что мир — это огромные часы.
Если знать положение каждой шестерёнки сейчас, можно вычислить, где она была вчера и где будет завтра.
Поэтому математика предсказывает будущее: она открывает вечные законы, которые сам Бог задал раз и навсегда.
--- Фрагмент 25 ---
Как случайность разрушила уверенность в предсказуемом мире
Когда XIX век верил, что будущее можно вычислить, как часы, природа подкинула сюрприз: оказалось, мир полон «особых точек» — моментов, когда крошечный толчок меняет всё. Камень на вершине горы, спичка в сухом лесу, случайное слово, ген-«переключатель» — достаточно лёгкого пинка, и система уходит в неконтролируемый хаос. Ученый Максвелл предупреждал: если физика продолжит игнорировать такие «щели» в законах, детерминизм рухнет. Он оказался прав.
Статистика пришла на смену жёсткому предсказанию. Страховщики не знают, когда умрёт конкретный человек, но по тысячам биографий точно рассчитывают риск и ставят цену полиса. То же случилось с газом: миллиарды молекул ведут себя строго по законам механики, но считать каждую невозможно; проще описать их средним поведением. Первым так сделал Больцман, но современники обозвали его «математическим террористом».
Атомный мир окончательно добил старую уверенность. Радиоактивный распад, странное двойное поведение электрона, «скачки» внутри атома — всё это нельзя предсказать точно. Принцип неопределённости Гейзенберга поставил жирную точку: мы не просто не умеем измерить причину, её просто нет. Физика может лишь сказать «с 95 % вероятностью частица окажется здесь». Точные траектории существуют только для больших сборищ частиц; одиночная частица живёт по законам случая.
--- Фрагмент 26 ---
Квантовая революция: за что боролись Эйнштейн и компания
О чём спор
Крупнейшие физики XX века разделились на два лагеря. Большинство (Бор, Гейзенберг, Паули) сказали: в мире атомов всё решает случай — электрон «сам выбирает», куда полетит. Меньшинство во главе с Эйнштейном возражало: «Природа не играет в кости!» Они верили, что за видимым хаосом скрываются точные, но пока невидимые механизмы, как в старой доброй ньютоновской механике.
Почему Эйнштейн не сдавался...
--- Фрагмент 27 ---
Как наука меняет наши глаза и цифры управляют миром
Коротко о главном
Классическая физика верила: формулы показывают, «что есть». Квантовая физика уточнила: формулы показывают, «что мы видим». Логические позитивисты добавили: смысл любого утверждения – это способ его проверить. Итог: наше знание не о «вещах в себе», а о том, как они проявляются в опыте.
Почему это важно для простого человека ...
--- Фрагмент 28 ---
Что скрывается за этими длинными списками книг
Перед вами – не обычная глава, а «карта» научной революции в четырёх актах. Каждая колонка – это один виток человеческого понимания природы.
Акт первый: Галилей и Декарт учат нас спрашивать «как?» вместо «зачем?».
Акт второй: Ньютон показывает, что весь мир движется по одним и тем же математическим правилам.
--- Фрагмент 29 ---
Как устроены атомы и почему они не распадаются
Физики XX века столкнулись с загадкой: по законам обычной физики электроны в атоме должны терять энергию и падать на ядро, но этого не происходит. Решение нашла квантовая механика.
Бор объяснил, что электроны движутся по особым «разрешённым» орбитам и не излучают энергию. Де Бройль добавил: каждая частица одновременно является и волной. Это как если бы теннисный мяч вдруг вёл себя как волна на воде. Опыты показали: поток электронов действительно создаёт картину волн, когда проходит через тонкую плёнку.
Следующий шаг сделал Шрёдингер. Он записал «волновое уравнение» — формулу, которая предсказывает, где в атоме можно найти электрон. Гейзенберг уточнил: мы не можем одновременно точно знать, где находится частица и куда она летит. Чем точнее одно, тем размытей другое. Это не недостаток приборов, а свойство самой природы.
--- Фрагмент 30 ---
Как устроена наука: три взгляда на правду
Что делает теорию научной
Томас Кун показал, что наука развивается не плавно, а скачками. Сначала учёные работают в рамках одной «картинки мира» (парадигмы), а потом внезапно переходят на совершенно новую. Пример: Эйнштейн не подправил Ньютона, а предложил другой взгляд на пространство и время.
Карл Поппер добавил простой тест: если теорию нельзя опровергнуть экспериментом, она не наука. По этому правилу психоанализ и марксизм выглядят не как наука, а как системы, которые могут объяснить всё что угодно. Квантовая механика, наоборот, рискует: она даёт точные цифры, которые легко проверить.
--- Фрагмент 31 ---
Краткое введение
Это алфавитный список научных и философских «точек опоры» — от античности до квантовой физики. Каждая строка — это ключ к большой идее или открытию. Ниже — самые важные «ключи» и что они открывают.
Главные идеи упрощённо ...
1. Как люди узнают мир
--- Фрагмент 32 ---
Перед вами не текст, а алфавитный указатель имён. Он служит обычной справочной целью: быстро найти, на каких страницах книги упоминается тот или иной учёный, философ или исторический деятель. Ни рассказа, ни развёрнутой мысли здесь нет — только фамилии и номера страниц.
Как пользоваться
1. Выберите нужную персону (например, «Эйнштейн»).
2. Посмотрите цифры после фамилии (у Эйнштейна их больше двух десятков).
Тема: Математика, физика и философия
Стиль изложения: Обучающий
Количество фрагментов: 32
Дата создания: 2025-09-13
Как увидеть Гугол- Машина де Брюина1
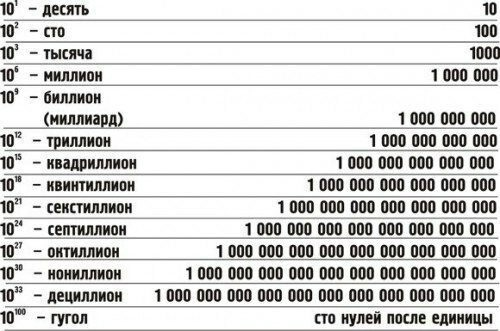
С какими цифрами мы обычно сталкиваемся в повседневной жизни? От десятков до миллиардов. Может, где-то проплывет триллион или даже квинтилион. Но есть одно число, которое не даёт покоя ученым. И это число — гугол. Казалось бы, простая цифра: 10 в степени 100.А теперь давайте попробуем разложить эту степень. В числовом виде это будет: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Да, это единица и сто нулей. Число настолько большое, что даже число атомов в известной части Вселенной меньше — по подсчетам, от 10 в 79 до 10 в 81.
И вот однажды одному ютуберу, Даниэлю де Брюину, пришла в голову светлая идея: а как можно визуализировать столь огромное число? И он построил свою "адскую машинку". Сама идея механизма очень проста. Он содержит ручку, которую нужно проворачивать, и 100 шестеренок с передаточным числом 10. Когда вы поворачиваете первую шестеренку, следующая шестеренка проворачивается со скоростью 1/10, то есть 10 полных вращений первой шестеренки приводят к единственному повороту второй.В итоге, чтобы провернуть последнее колесо хоть на зубчик, первое колесо должно совершить полный оборот ровно 1 гугол раз.
При всей изящности решения у такой установки есть фундаментальный недостаток — никто и никогда не увидит результатов её работы. Потому что если представить, что ручка проворачивается со скоростью 1 оборот в секунду, потребуется лишь 317097919837645865043125317097919837645865043125317097919837645865043125317097919837645865043 лет, чтобы последняя шестеренка начала движение. При этом энергии, затраченной на вращение, потребуется больше, чем содержит вся наша Вселенная. Даже если бы чисто гипотетически механизм вращался со скоростью 1 оборот в секунду с момента формирования Земли, а это 4,6 млрд лет, то всего лишь 18-я шестеренка провернулась бы только на половину.В итоге у Дэниэля получился механизм, который одновременно является как гениальным, так и совершенно бесполезным.
Автор - @Shyxart
Подписывайтесь, чтобы не пропустить новые посты!
Замена тэна
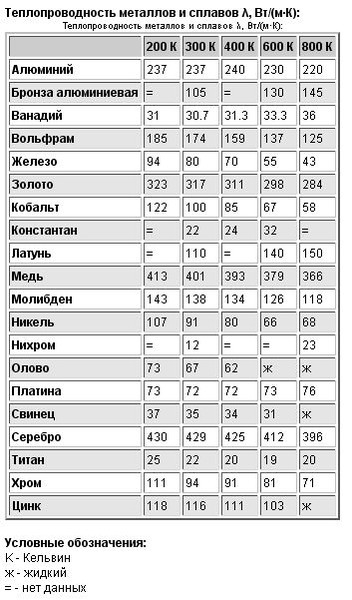
Сгорел тэн на обогревателе, как оказалось - это была слюдяная трубка патронного типа с нихромовой спиралью внутри (типа как в паяльнике) мощностью 500 Вт, длиной около 500 мм и диаметром 12-13 мм, вставленная в металлическую колбу масляного радиатора. Аналогичный металлический найти не получается. Есть короче в два раза. Не будет ли он перегреваться при той же мощности? Ведь теплопроводность металлов гораздо больше слюды
Ответ на пост «Российские физики установили мировой рекорд квантовых вычислений»1
Сначала победим всех в квантовых вычислениях, потом изобретем межпланетные перелеты, далее телепортация, регенерация органов, регенерация клеток тела, вечная жизнь. И после этого все заживут вечно и счастливо, правда пару недель в году придется воду греть в чайнике и мыться из ковшика