Думай медленно, решай быстро. Часть 3.

Далее Канеман и Тверски начинают разворачивать свою теорию подхода к экономике, которую они назвали теорией перспектив.

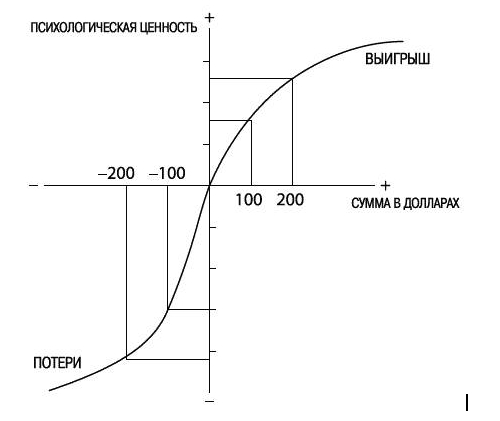
Канеман начинает с того, что некоторые экономические теории предполагают, что люди - рациональные агенты. Т.е. рационально оценивают полезность исходов, умножая вероятность события на его ценность, и выбирают вариант с максимальной ожидаемой полезностью. Например, если тебе предлагают 50% шанс выиграть 100 долларов или гарантированные 40 долларов, приверженец рациональных агентов в экономике сказал бы, что ты сравнишь 0.5 × 100 = 50$ с 40$ и выберешь лотерею. Но в реальности люди часто берут гарантированные 40 долларов. Почему? Канеман отвечает: потому что мы не думаем в терминах абстрактной полезности, а реагируем на изменения относительно текущего состояния — прибыли или потери. Авторы книги заметили, что люди оценивают исходы не в абсолютных величинах (сколько у них будет в итоге), а в относительных — как выигрыш или проигрыш по сравнению с точкой отсчёта (обычно это их текущее богатство).

Канеман объясняет на примере экономической модели Бернулли, что эта модельне учитывает асимметрию. Для Бернулли потеря 100 долларов и выигрыш 100 долларов — просто противоположные величины с одинаковым весом. Но в реальности потеря бьёт по нам эмоционально в разы сильнее, чем радость от выигрыша. Теория перспектив вводит «функцию ценности», где кривая для потерь круче, чем для выигрышей, и точка отсчёта — не ноль, а текущее состояние человека. Это ключевое отличие от Бернулли.

Ещё одна «ошибка Бернулли» — игнорирование того, как люди воспринимают вероятности. Канеман показывает, что мы не оцениваем шансы линейно, как в математике. Маленькие вероятности (скажем, 1% шанс выиграть миллион) переоцениваются, а средние (50%) недооцениваются. Бернулли считал, что мы просто умножаем вероятность на исход, но теория перспектив вводит «весовую функцию», где люди искажают вероятности из-за эмоций и когнитивных искажений. Например, лотерейный билет манит, хотя шанс выиграть ничтожен, потому что 1% кажется «реальным», а 0% — «невозможным».

Эффект владения

Представим, что вам подарили кружку. Если бы вы покупали её сами, то дали бы, скажем, 5 долларов. Но теперь, когда она ваша, вы не отдадите её дешевле, чем за 10. Это и есть эффект владения: как только что-то становится «твоим», его ценность в ваших глазах растёт. Канеман ссылается на эксперименты, которые проводили вместе с экономистом Ричардом Талером: студентам давали кружки, а потом предлагали продать или купить их. Те, кто владел кружками, запрашивали в два-три раза больше, чем те, кто хотел их приобрести.

Канеман объясняет это через теорию перспектив и неприятие потерь. Когда ты чем-то владеешь, отказ от этого воспринимается как потеря, а потери, как он показал в «Ошибках Бернулли», бьют по нам сильнее, чем радость от эквивалентного выигрыша. Продать кружку за 5 долларов — это не просто сделка, а эмоциональная «боль» от расставания с ней, и эта боль требует компенсации. В то же время покупка — это выигрыш, который не так сильно нас волнует. Вспомним, как мы устанавливаем цены на вторичном рынке на вещи, которые нам принадлежали довольно долго. Мало кто пытается оценить реальную рыночную стоимость товара, скорее ориентируясь на цену похожих товаров и стараясь продать никак не меньше этой отметки. Более эмоциональная Система 1 в действии.

Парадокс Алле

Суть парадокса в том, что люди делают противоречивые выборы в ситуациях с одинаковой математической структурой, если исходы представлены по-разному. Алле предложил два набора лотерей, чтобы это продемонстрировать.

Ситуация 1:
Вариант A: 100% шанс выиграть 1 миллион долларов.
Вариант B: 10% шанс выиграть 5 миллионов долларов, 89% шанс выиграть 1 миллион долларов, 1% шанс ничего не получить.

Большинство людей выбирают A — гарантированный миллион, хотя ожидаемая полезность B выше (0.10 × 5M + 0.89 × 1M + 0.01 × 0 = 1.39 миллиона против 1 миллиона).

Ситуация 2:
Вариант C: 11% шанс выиграть 1 миллион долларов, 89% шанс ничего не получить.
Вариант D: 10% шанс выиграть 5 миллионов долларов, 90% шанс ничего не получить.

Здесь большинство предпочитают D — шанс на 5 миллионов, хотя ожидаемая полезность C (0.11 × 1M = 110 тысяч) чуть выше, чем D (0.10 × 5M = 500 тысяч), если учитывать только вероятности и суммы.

Канеман объясняет, что эти выборы противоречат принципу ожидаемой полезности. Согласно модели Бернулли, если человек выбирает A в первой ситуации (предпочитая надёжность), он должен выбрать C во второй (где тоже больше надёжности в рамках шанса). А если он выбирает B (риск ради большего выигрыша), то должен взять D. Но люди выбирают A и D, что ломает логику рациональности.

Это происходит потому, что в первой ситуации A кажется выигрышем (гарантированный миллион), а B включает риск потери (1% шанс остаться ни с чем), что пугает из-за неприятия потерь. Во второй ситуации оба варианта — лотереи с высоким шансом ничего не получить, так что D выглядит привлекательнее благодаря большому выигрышу (5 миллионов), а разница между 11% и 10% кажется несущественной. Система 1 искажает вероятности: в первом случае надёжность перевешивает, во втором — эмоции от возможного джекпота.

Общий вывод, который тут можно сделать - люди иногда склонны переплатить за некие гарантии и стабильность, хотя это и не рационально. Относится ли к этому случаю оплата какой-либо страховки? Похоже, что да. И, получается, это ещё один рычаг манипуляций, играть на страхах что-то потерять, «раздувая» некие негативные последствия отсутствия страховки.

Редкие события

Канеман обращает внимание на то, что люди часто переоценивают маловероятные исходы, особенно если они эмоционально заряжены. Система 1 придаёт слишком большой вес редким событиям — вроде выигрыша в лотерею или авиакатастрофы, — потому что они яркие и легко всплывают в памяти (эвристика доступности). Теория перспектив вводит «весовую функцию»: вместо объективных вероятностей (например, 1% шанс) мы субъективно их раздуваем, что объясняет, почему люди покупают лотерейные билеты или страховки от почти невозможных рисков.

Пример: шанс выиграть миллион кажется «реальным», хотя он ничтожен, а 0% и 1% воспринимаются как разные миры.

Яркие исходы

Также мы часто переоцениваем значимость экстремальных результатов — больших выигрышей или потерь, — даже если их вероятность мала. Это связано с неприятием потерь и искажением вероятностей из теории перспектив. Если исход драматичен (например, потерять всё или сорвать куш), он затмевает скучную середину, и Система 1 фокусируется на нём, игнорируя статистику. Пример: люди скорее выберут 5% шанс на 10 миллионов долларов, чем гарантированные 100 тысяч, хотя ожидаемая ценность ниже, потому что «яркость» миллиона манит сильнее.

“Сожаление — одна из противоречивых эмоций, возникающих, когда доступны альтернативы реальности.”

Это эмоциональное состояние хорошо описано двумя голландскими психологами, указавшими, что сожаление «сопровождается ощущением, что нужно было думать раньше, гнетущим чувством, мыслями об ошибке и упущенных возможностях, желанием дать себе пинка и исправить ошибку, желанием вернуться назад и получить второй шанс».

Это искажение проявляется во многих контекстах. Покупатели, помня о возможных сожалениях в случае неправильного выбора, упорно придерживаются традиционного выбора, отдавая предпочтение брендовым товарам перед малоизвестными. Поведение держателя акций к концу года тоже показывает эффект предвкушаемой оценки: он пытается очистить инвестиционный портфель от малоизвестных и сомнительных акций.

Инверсия предпочтений

Явление, когда люди меняют свои предпочтения в зависимости от того, как им представлена задача выбора, даже если логически их выбор должен оставаться неизменным.

Суть инверсии предпочтений связана с тем, как Система 1 реагирует на формулировку вопроса или контекст. Канеман приводит примеры, где изменение описания — например, акцент на выигрышах или потерях — переворачивает выбор людей. Один из классических случаев — эксперимент с «азиатской болезнью» (хотя он больше известен из других глав):

Вариант 1 (выигрыш):
А: Спасём 200 человек из 600 точно.
Б: 33% шанс спасти всех 600, 66% шанс никого не спасти.

Люди чаще выбирают А — гарантированное спасение.

Вариант 2 (потери):
С: 400 человек из 600 точно умрут.
D: 33% шанс, что никто не умрёт, 66% шанс, что все 600 умрут.

Здесь чаще выбирают D — шанс избежать потерь.

Хотя математически варианты А и С, а также Б и D идентичны (200 спасённых = 400 умерших), люди меняют предпочтения: в первом случае избегают риска ради выигрыша, во втором рискуют, чтобы избежать потерь.

Эффект фрейминга
Когнитивное искажение, при котором наш выбор зависит от того, как представлена информация, даже если суть остаётся той же. Канеман показывает, что Система 1 реагирует на формулировку, а не на объективные факты.

Пример:
Два описания краткосрочных исходов хирургического вмешательства выглядели так.

Месячный уровень выживаемости — 90 %.
Смертность составляет 10 % в первый месяц.

Операция казалась более привлекательной в рамках первой формулировки (ее выбрали 84 % врачей), чем во второй (50 % предпочли радиотерапию). Логическая эквивалентность двух описаний очевидна, и связанный с реальностью человек, принимая решение, сделает один и тот же выбор, какую бы версию ему ни показали. Но, как известно, Система 1 редко остается безучастной к эмоциональным словам: «смертность» — плохо, «выживание» — хорошо; «выживаемость в 90 % случаев» звучит ободряюще, а «смертность в 10 % случаев» — пугает.

Телеграм канал - Юмор ТВ 404

Продолжаю конспект книги.

Даниэль Канеман описывает эвристики как ментальные сокращения, которые позволяют людям быстро принимать решения без глубокого анализа. Эти упрощённые стратегии мышления помогают нам ориентироваться в мире, но часто приводят к систематическим ошибкам (когнитивным искажениям).

Эвристика подстановки вопросов:
Когда мы сталкиваемся со сложным вопросом, требующим детального анализа, наш мозг бессознательно подменяет его более простым, но похожим. В итоге мы отвечаем не на тот вопрос, который нам задали, а на тот, который легче обработать.

Пример: основной вопрос — «Стоит ли инвестировать в этот стартап?». Вопрос, на который происходит подмена, — «Насколько уверенно держится организатор стартапа на презентации для инвесторов?». В результате инвестор вкладывается в стартап, потому что основатель харизматичен, а не потому что проект имеет реальные перспективы.

Эвристика аффекта: ещё один пример подмены.
Вместо того чтобы тщательно взвешивать плюсы и минусы, человек опирается на своё эмоциональное отношение к объекту или ситуации. Если что-то вызывает положительные эмоции, мы склонны недооценивать риски, а если негативные — переоценивать их.

Закон малых чисел:
Люди склонны верить, что маленькая выборка (например, несколько примеров) отражает общую закономерность так же точно, как большая выборка. Это приводит к завышенной уверенности в наших выводах и к ошибкам в прогнозах.

Очень интересная когнитивная ошибка, одна из моих любимых. Именно из-за неё при проведении эксперимента или статистического анализа важно оценивать репрезентативность выборки (кстати, ещё один способ манипулировать мнением масс — делать выводы на нерепрезентативных выборках). Сюда же, судя по всему, относится проблема «сигнал-шум», которую описывает в своей книге «Сигнал и шум» Нейт Сильвер. Дело в том, что малые выборки в большей степени подвержены случайным колебаниям — «шуму», в отличие от большой выборки, где влияние «шума» уменьшается. Из-за этого малые выборки больше подвержены экстремумам.

Ещё один пример: фраза «По результатам телефонного опроса пенсионеров, 60% поддерживают президента». Скорее всего, человек, услышавший эту фразу, придёт к мнению, что в целом пенсионеры поддерживают президента. Однако важно узнать, сколько пенсионеров от общего их числа участвовали в опросе, как формулировали вопрос (как будет ясно дальше, это тоже важно), по какому именно вопросу они его поддерживают и, наконец, как мнение пенсионеров соотносится с мнением остальных граждан.

Иллюзия закономерности:
Тоже относится к закону малых чисел, но проявляется в нашем мышлении буквально каждую минуту. Дело в том, что наше сознание настроено на построение прогнозов — это фундаментально важный процесс работы нашего мозга. А для построения прогноза необходимо понимать причинно-следственную связь между явлениями (каузальная связь). Под прогнозами тут имеются в виду не прогнозы курса валют или чего-то такого. Прогнозы могут быть самого разного вида: например, чтобы отбить теннисный мяч, необходимо построить прогноз о его траектории, чтобы осуществить любую коммуникацию, необходимо построить прогноз о возможных исходах (замечали за собой, как иногда вы планируете, что сказать, какую фразу лучше выбрать?).

Так вот, с поиском причинно-следственной связи наш мозг очень часто ошибается. Вспомните все суеверия, которые вам встречались: счастливая рубашка, ритуал перед важным событием и т.д. Сюда же относится оценка вероятности в игре в рулетку или в кости: игроки верят, что после нескольких проигрышей должна выпасть победа (ошибка игрока). На самом деле много чего относится к этой ошибке: и лженаучные теории, и религиозные концепции, и теории заговора.

Эффект привязки:
Это когнитивное искажение, при котором первая полученная информация (число, факт, мнение) влияет на последующие оценки и решения, даже если она нерелевантна. Наш мозг бессознательно использует первоначальную информацию как «якорь» и корректирует последующие оценки относительно него. Однако эта корректировка часто недостаточна, из-за чего мы остаёмся «привязанными» к исходному значению.

Примеры:
- Магазины сначала показывают завышенную цену, а затем дают «скидку». Мы воспринимаем новую цену как выгодную, даже если она остаётся высокой. - Первая озвученная цифра в сделке (например, при покупке машины) влияет на конечную цену.

- Первая озвученная цифра в сделке (например, при покупке машины) влияет на конечную цену.

На основе этой привязки профессиональные переговорщики добиваются выгодных для себя сделок. Встречали такой лайфхак: попросить о крупной просьбе, чтобы потом человек с большей долей вероятности согласился на более мелкую просьбу, но которая и была целевой? Об этой технике, например, упоминает Роберт Чалдини в книге «Психология влияния».

Эвристика доступности:
Ещё одна эвристика, которая настолько фундаментальна, настолько сильно влияет на наше мышление, что знать её просто необходимо. Суть в том, что информация, которая вспоминается легко, априори считается более достоверной. Чтобы информация вспоминалась легко, ей достаточно быть интересной для вас, или драматичной (катастрофа), или просто быть привязанной к вашему личному опыту. Если информация обладает какими-то из этих атрибутов в любом их сочетании, она будет извлечена легче и в большей степени повлияет на ваши суждения.

Тут позволю себе немного углубиться в нейрофизиологию. Не секрет, что наш мозг представляет из себя набор нейросетей со сложной структурой взаимодействий между собой. Нейросети, которые задействованы чаще или задействованы с эмоциональным аспектом (грубо говоря, при когерентной работе с лимбической системой), в дальнейшем легче активируются. Активация этих сетей чаще всего происходит неосознанно, при пассивной обработке. Таким образом получается, что чем больше вы потребляете непроверенной информации, тем выше шанс потом вспомнить именно её. Это — основной принцип работы рекламы: заспамить нас названием бренда, чтобы потом, когда нам понадобится какой-либо продукт, мы вспомнили именно его, а следовательно, посчитали его более качественным (помните правило рекламы: не меньше трёх повторений названия?).

Пример:
По новостям рассказывают о крушении самолёта. На какое-то время вы будете считать самолёт более опасным транспортом, чем считали до просмотра новостей. Однако в новостях не сообщают о тысячах успешных перелётов каждый день, а значит, вы не можете оценить статистику безопасности корректно.

Эксперты:
Здесь кратко. У экспертов есть как преимущества в оценке профильной информации, так и недостатки. Эксперты часто подвержены специфическим когнитивным ошибкам в дополнение к «общим», что делает их мнение столь же требующим проверки, как и мнение любого другого человека. Если обобщить с предыдущими когнитивными ошибками, то получается, что, при прослушивании чьего-то мнения, мы не только делаем вывод, не проверяя факты, но ещё и склонны менять степень доверия из-за своего личного отношения к оратору.

Меньше лучше. Ошибка конъюнкции:
Линде 31 год, она не замужем, откровенная и очень умная. В университете изучала философию. Будучи студенткой, она уделяла много внимания вопросам дискриминации и социальной справедливости, а также участвовала в демонстрациях против использования ядерного оружия.

Как вы думаете, какое описание вероятнее?
Линда — кассир.
Линда — кассир в банке и активистка феминистского движения.

В проведённом Канеманом и Тверски эксперименте испытуемые чаще выбирали вариант «Кассир и активистка феминистского движения».
Однако, если обратиться к формальной логике, то вариант «А и Б» всегда менее вероятен, чем вариант «только А».

Регрессия к среднему:
Суть в том, что в любой системе с элементами случайности результаты колеблются вокруг среднего значения. Если что-то уходит далеко в крайность — очень плохо или очень хорошо, — следующий исход с высокой вероятностью будет ближе к норме. Это не магия и не чья-то заслуга, а чистая статистика. Канеман приводит пример с пилотами: инструктор заметил, что после похвалы за отличный манёвр ученик часто летал хуже, а после критики за ошибку — лучше. Он решил, что похвала расслабляет, а критика мотивирует. На деле это была регрессия: выдающийся успех или провал и так сменялись бы средним результатом, без всякого влияния слов.

Хочется сделать ремарку по поводу статистических методов. Канеман часто противопоставляет нерациональное мышление Системы 1 статистическим методам. Однако Джудея Перл в книге «Думай, почему» указывает на множество проблем статистики как метода формирования суждений: от той же нерепрезентативности выборки до парадокса Симпсона.

Иллюзия понимания прошлого:
Это концепция, которую Канеман развивал в своих работах, и она перекликается с идеями Нассима Талеба. Если кратко, Талеб называет иллюзию понимания «нарративной ошибкой»: мы цепляемся за объяснения, которые звучат красиво, вместо того чтобы признать хаос и случайность. Канеман называет это «ретроспективной иллюзией»: нам кажется, что мир проще и понятнее, чем он есть на самом деле, потому что мы видим только то, что уже произошло. Иными словами, это иллюзия того, что прошлое можно понять однозначно и полностью, что ведёт к неверным прогнозам в будущем. Здесь стоит вернуться к фундаментальному принципу работы нашего мозга: поиску причинности явлений для построения прогнозов. Поэтому нам легко найти причины всех исторических явлений. Но это только нам кажется, что мы их нашли. Именно поэтому в научном методе важны принципы системности и историчности: мы должны стараться найти все возможные факторы влияния на исследуемые явления, даже казалось бы незначительные. Об этом великолепно пишет Джудея Перл в книге «Думай, почему» (конспект обязательно будет). Он показывает сложность нахождения причинно-следственных связей, вводя такие понятия: запутывающие переменные, коллайдеры, опосредование.

Ошибка планирования:
Ох, как часто я на неё попадался!
Это склонность недооценивать время, ресурсы или сложности, необходимые для выполнения задачи. Пример из жизни: при взятии заказа на web-продукт без чёткого технического задания я каждый раз оценивал сроки сильно меньше, чем выходило на самом деле. Теперь я закладываю в три раза больше сроков и ресурсов по сравнению с первоначальным мнением. Суть ошибки в том, что мы опираемся на оптимистичные сценарии, которые рисует наш разум, вместо того чтобы учитывать реальные данные или прошлый опыт.

Иллюзия значимости:
Это склонность людей переоценивать точность своих суждений, прогнозов или интерпретаций, даже когда у них недостаточно информации или доказательств. Мы часто уверены в своих решениях, даже если они основаны на случайных данных или неполной картине.

Канеман объясняет, что это связано с работой Системы 1, которая стремится быстро находить закономерности и делать выводы, даже если они необоснованны. Система 2 могла бы проверить эти выводы, но часто ленится или игнорирует необходимость анализа.

Пример:
Эксперты на фондовом рынке часто делают прогнозы, основываясь на ограниченных данных, и уверены в их точности. Однако исследования показывают, что такие прогнозы редко бывают точнее случайного угадывания.

Продолжение следует...

#comment_332741006