Используя знаки сложения, вычитания и умножения, а также скобки, запишите число 500 с помощью семи цифр 4. Склеивать цифры нельзя.
А можно ли обойтись шестью четвёрками, если разрешить использовать ещё и деление, а также склеивать цифры?
Каждый кто учился в автошколе в последние годы( и я тоже) сталкивается с такой проблемой как словесные ребусы. Типо команды развернись на нерегулируемом перекрестке, имея ввиду кольцо, или развернись на дороге с односторонним движением. Почему экзамен на вождение стал похож на какой то ребус, где в каждой команде обязательно есть подвох.
Действительно ли это делается для блага водителей или это какой то мастшабный развод на бабки?
Если ребенок не сдал экзамен, кого винить? Учителя? Родителя? Ребенка? Школу? Систему образования? Ретроградный Меркурий?
Пришли результаты ОГЭ по предметам по выбору. А с ними и сообщение от администратора. Не пытайтесь это понять. Это нужно просто принять🙃.
Как оказалось, не все поняли. Разъясняю. Если ребёнок имеет годовую оценку 3, а экзамен сдал на 5, в аттестат идёт 5. Если годовая 3, а экзамен 5, в аттестат - 5. То есть, не среднее арифметическое, как было всегда, а высший балл. Упростили жизнь детям - проще некуда. Как говорится, всё для вас. Только русский и математика по среднему арифметическому рассчитываются.
Помните, в начале апреля по стране широко обсуждались новые правила приёма в 10 класс? Подразумевалось, что эти правила сделают отбор более жёстким. Мы, учителя, обрадовались, что в старшей школе останутся мотивированные дети. Родители, наоборот, волновались и возмущались.
Ну и вот. Без комментариев.
Никогда такого не было, и вот опять.
В третьем номере журнала "Квант" за 1978 год предлагалась следующая задача:
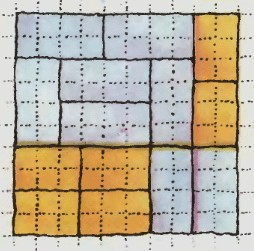
"Из восьми прямоугольников размером 2×4 и шести прямоугольников размером 2×3 Лёня сложил квадрат размером 10×10. Посмотрев на этот квадрат внимательно, он обнаружил, что в двух случаях стороны этих прямоугольников образуют отрезки, соединяющие противоположные стороны квадрата. Это показалось Лёне некрасивым, и он решил сложить из данных четырнадцати прямоугольников тот же квадрат, но уже так, чтобы подобных отрезков не было. Помогите Лёне, ребята!"
К этой задаче прилагалась катринка (см. катринку вверху):
Вот официальное решение из следующего номера "Кванта" (см. катринку в внизу слева):
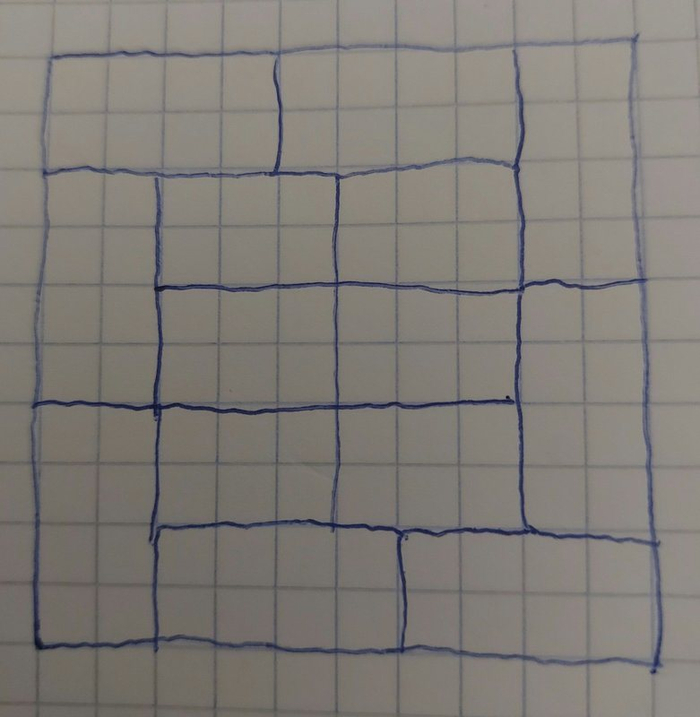
Хочу предложить своё решение, более красивое и симметричное, на мой взгляд (простите, что от руки и небрежно, см. катринку внизу справа):
Только что я на практики доказал, что продуктивность студента обратно пропорционально времени, оставшемуся до экзамена - за одну ночь родил всю текстовую часть дипломного проекта, которую до этого не мог сделать полгода. Сдавать сегодня утром, осталось только презентацию накидать, но это Ctrl+C Ctrl+V и картинок натырить.
У каких примориалов, увеличенных на 2, сумма делителей будет нечётной?
Ясно, что нечётную сумму делителей дают либо квадраты, либо удвоенные квадраты.
Вот первые 4 решения: 4, 8, 32, 2312.
Существует ли пятое и как его найти?
