Теорема Эйлера-Савари в трактовке советских «файдоров» …
Сие: вариант этюда для «Пикабу»…
Спросим всепроникновенную "Алису" за теорему Эйлера-Савари!
Рис.1
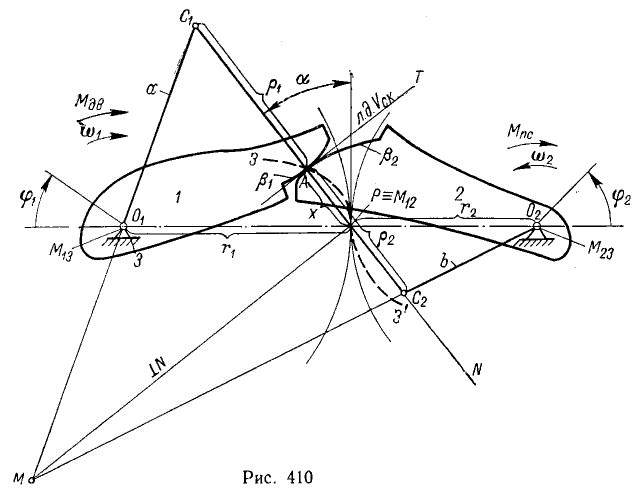
"... радиусами кривизны профилей"?! Вероятно, «первоисточником» такой трактовки теоремы Эйлера-Савари явились труды знаменитого советского механика тов. Н.И.Колчина. Например, фундаментальный труд «Механика машин». Рисунок из т.1 «Механики машин» 1972-го года издания:
Рис.2
Нетрудно понять, что на приведённом рисунке - построение Бобилье для точек С1 и С2: точка С2 - центр кривизны траектории, которую описывает точка С1 при обкаточном движении тела 1 вокруг неподвижного тела2. Разумеется, точка С1 «автоматически» будет центром кривизны траектории точки С2 в случае неподвижного тела 1 и «обкатывающего» тела 2.
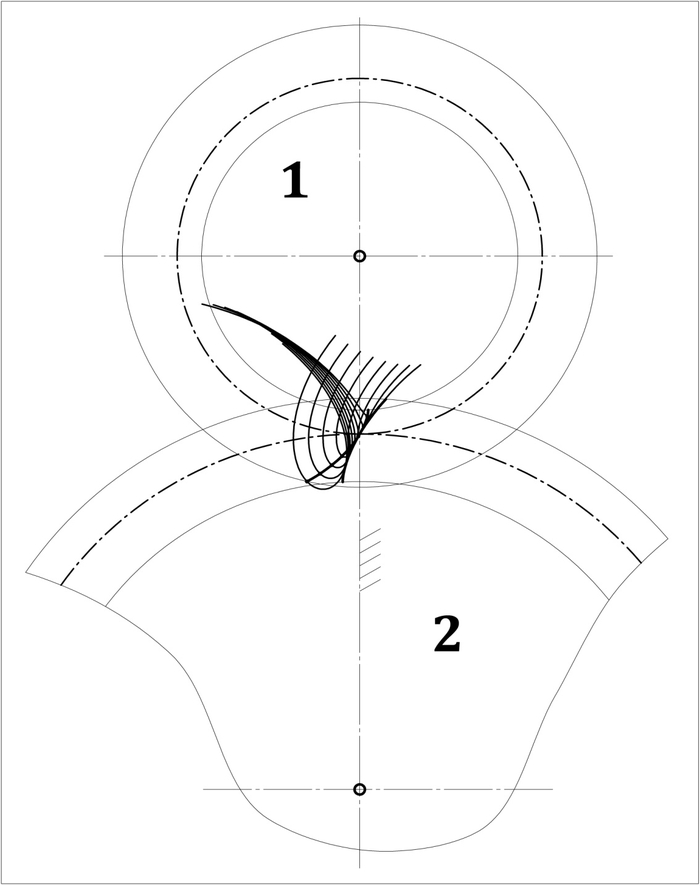
Вопиющую ошибочность колчинской трактовки теоремы Эйлера-Савари(Ф.!) нетрудно понять из рис.3, на котором построены циклоиды, описываемые точками на сопряжённом профиле (например, эвольвентном) подвижного зубчатого колеса 1 при обкатке его относительно (условно) неподвижного колеса 2:
Рис.3
Замечание: очевидно, что профиль второго колеса есть огибающая семейства циклоид от точек на профиле колеса 1.
Непонимание сути (красивейшей !) теоремы Эйлера-Савари, вероятно, приводит тов. Н.И.Колчина к такому ошибочному суждению:
Рис.4
Во-первых, «на одном из колёс профиль зубьев» - совершенно не произвольный. Согласно теореме Виллиса (о мгновенном передаточном отношении - главная теорема зацепления), профиль «на одном из колёс» должен быть таким, чтобы нормаль к этому профилю в каждом угловом положении колеса на всём интервале касания с сопряжённым профилем проходила через полюс зацепления (мгновенный - в общем случае). Фактически же (см. «Замечание» выше), профиль «на одном из колёс» порождает профиль на другом колесе.
Во-вторых, как показано на рис.3, теорема Эйлера-Савари - суть элегантный способ нахождения центра кривизны траектории (циклоиды) данной конкретной точки на обкатывающем колесе. Разумеется, этот центр кривизны может быть вычислен методами аналитической геометрии. В общем случае - при переменном передаточном отношении - теорема Эйлера-Савари даёт ограничение на локальную кривизну сопряжённых профилей.
Исходя из вышесказанного, можно сделать такой вывод: геометрия сопряжённых профилей полностью следует из теоремы Виллиса. Теорема Эйлера-Савари при построении сопряжённых профилей может играть только сугубо вспомогательную роль.
………………………….
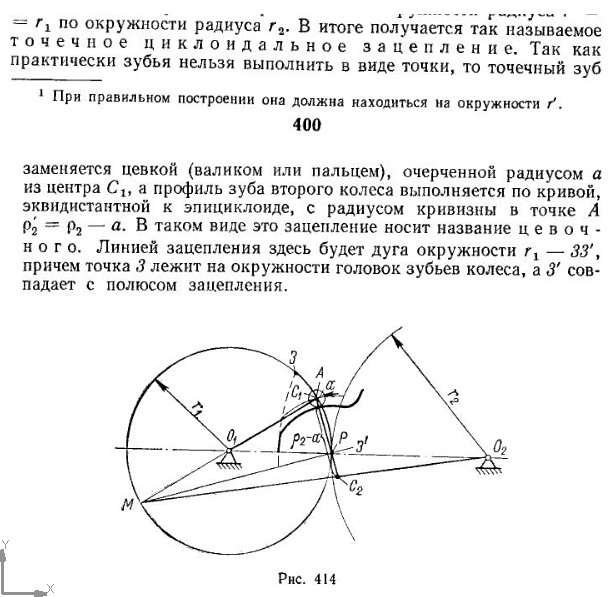
(Отметим, для примера, ещё одну очевидную ошибку тов. Н.И.Колчина:
Рис.5
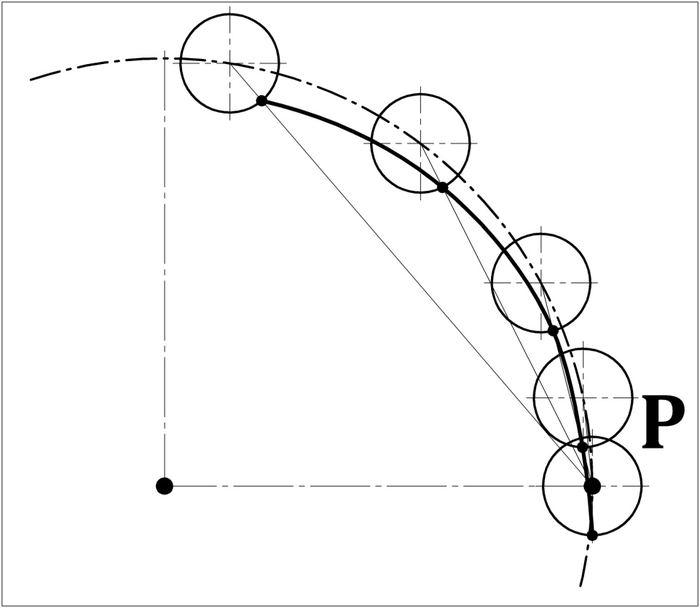
Почему линия зацепления цевочной передачи с цевкой ненулевого радиуса не будет дугой окружности r1:
Рис.6)
Так что…
(Ещё про «пёрлы» советских «файдоров» - на Дзен-канале «Добро» на вентилятор»... Там же ж: иллюстрации к сему писанию.)