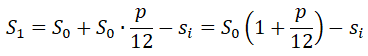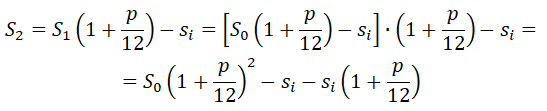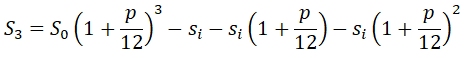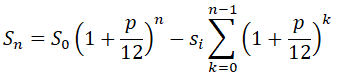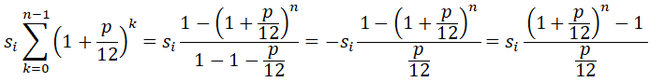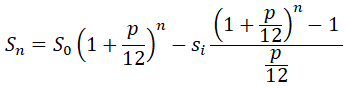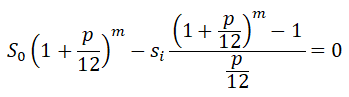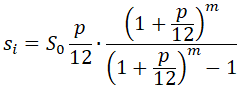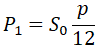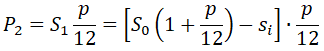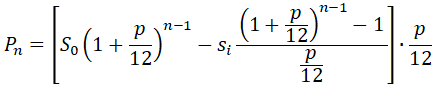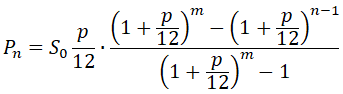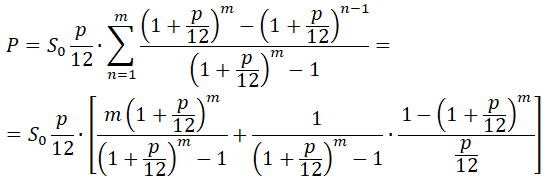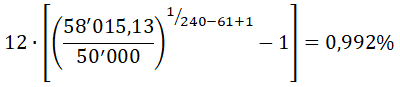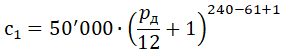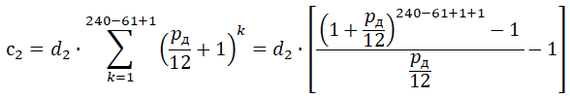Так уж получается, что далеко не все понимают важность досрочных платежей по ипотеке и как они влияют на суммарную переплату по кредиту. В моём предыдущем посте Про ипотеку я постарался описать механизм начисления процентов, но комментарии подсказывают, что не все моменты понятны.
Попробую развеять миф, что в первую половину срока кредита платятся проценты, а во вторую – тело кредита.
Для ЛЛ - в конце есть Выводы.
Буквально позавчера обращался к сотруднику банка по вопросу предоставления небольшого кредита на 3 года, так он без капли сомнения утверждал, что досрочно гасить кредит имеет смысл только в первой половине срока.
Пост большой, состоит из четырёх частей, в которых я постарался подробно описать расчёты и разобрать варианты на примере.
Кому не интересна математика – сразу переходим к частям 2-4 с графиками и рассмотренным примером. Подробную математику решил включить, чтобы желающие могли повторить расчёт для своих условий. Авось пригодится кому… А нет, так зря старался. :)
================================
Часть 1. Теория
Придётся пописать немного формул, чтобы любой со знанием математики на уровне 9-11 классов мог повторить проделанный расчёт.
Обозначим начальную сумму кредита S0, процент по кредиту p (p = 0÷1, что соответствует 0-100%) и количество месяцев, на который берётся кредит – m (целое число). Считаем, что проценты начисляются раз в месяц (для удобства), а не каждый день, как обычно в банках!
Тогда на конец первого месяца (или начало второго месяца, что одно и то же), после уплаты месячного платежа si, у нас останется кредит на сумму:
S0·p/12 – это начисленные проценты по кредиту за первый месяц. Отсюда следует, что тело кредита будет уменьшаться, только если si > S0·p/12. Если по кредиту каждый месяц, начиная с первого платить сумму S0·p/12, то кредит не закрыть никогда.
На конец второго месяца по аналогии с первым, уже будет сумма кредита:
А на конец третьего месяца:
Думаю, что трёх месяцев достаточно, чтобы увидеть зависимость и написать общее выражение для любого месяца n:
Второе слагаемое является суммой геометрической прогрессией (b1 = si, q = 1+p/12):
Учитывая геометрическую прогрессию, получаем формулу для расчёта тела кредита на конец любого месяца (при одинаковых ежемесячных платежах si):
Сумма ежемесячного платежа по кредиту (формула была приведена в предыдущем посте) рассчитывается из условия, что на окончания m-ного месяца (последнего) останется нулевая сумма кредита:
Теперь переплата по процентам.
За первый месяц будет начислено процентов:
За n-ный месяц (сумма от тела кредита, полученного на конец n-1 месяца!):
Куда подставляем нами полученное выражение для si, и после преобразований получим:
А суммарная переплата по процентам за весь кредит (с учётом суммы геометрической прогрессии):
Фух, сложное позади. Идём дальше…
================================
Часть 2. Базовый расчёт
Рассмотрим пример. Берём кредит на 1 млн. рублей под 12% годовых на срок 20 лет (240 месяцев).
Ежемесячный платёж составит si = 11’010,86 рубл., суммарная выплата по кредиту 240×si = 2’642’606’72 рубл., а сумма выплаченных процентов соответственно P = 1’642’606,72 рубл.
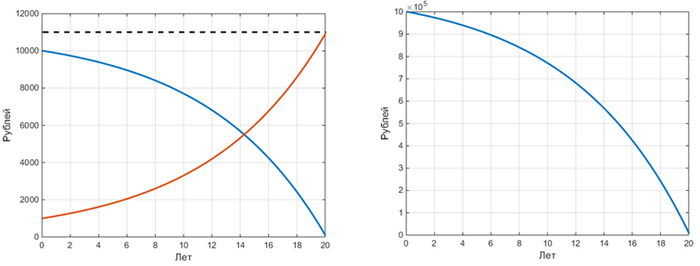
График платежей с величиной процентов по кредиту и телом кредита в каждом платеже, так любимый многими, (слева) и график уменьшения тела кредита (справа):
Можно заметить, что график уменьшения тела кредита с точностью до некоторого коэффициента (p/12 = 1% = 0,01) совпадает с графиком платежей по процентам.
Запомнили цифры?
Едем дальше…
================================
Часть 3. Досрочный платёж
А теперь давайте посмотрим, как скажутся дополнительно внесённые 50 тысяч по кредиту в конце пятого года (в 60 месяце).
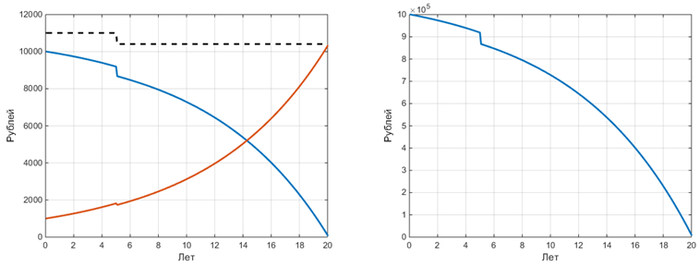
Так как срок кредиты мы уменьшать не будем, то снизится сумма ежемесячного платежа (на рисунках отмечаю чёрной пунктирной линией).
Ежемесячный платёж с 1 по 60 месяцы будет, как и в базовом расчёте 11’010,86 рубл., а с 61 по 240 – 10’410,78 рублей. Суммарная переплата по кредиту (проценты) составит 1’584’591,59 рублей. Если сравнивать с базовым расчётом, мы сэкономили 58’015,13 рубл.
Графики:
А с учётом внесённых 50 тыс. – заработали 8’015,13 рубл. Ради интереса можно посчитать процентную ставку, чтобы через (240-61+1) месяц у нас 50 тысяч дали доход 8 тыс. с копейками:
Получается, что намного эффективнее вложить эти 50 тысяч в депозит под 4%, чем досрочно заплатить за кредит. Но это только с первого взгляда…
Переходим к четвёртой части, где будем сравнивать потенциальных доход от наших «лишних» 50 тысяч.
================================
Часть 4. Так что выгоднее?
Сравнивать имеет смысл только для одинаковых условий. Основное: в каждой схеме считаем деньги на срок окончания базового кредита, т.е. через 240 месяцев! Условие второе – у нас каждый месяц в течение всего срока кредита есть сумма, соответствующая ежемесячному платежу по базовому расчёту, которую мы можем использовать на кредит или депозит.
Схема 1) Досрочно по кредиту платить не выгодно. Кладём 50 тыс на депозит и смотрим сколько будет на конец срока (процентную ставку по депозиту обозначим pд):
Схема 2) Платим досрочно 50 тыс. Тогда начиная со следующего месяца у нас появляется небольшая сумма d2 = 11’010,86 - 10’410,78 = 600,08 рубл., которую мы можем каждый оставшийся месяц кредита класть на вклад. На конец срока у нас будет (с учётом процентов по депозиту):
Схема 3) Платим досрочно 50 тыс. Тогда уже в 61 месяце у нас появляется небольшая сумма d3 = 11’010,86 - 10’410,78 = 600,08 рубл., которую мы также используем для уменьшения тела кредита. Это приводит к новому значению (меньшему) ежемесячного платежа в 62 месяце. Новую оставшуюся сумму в 62 месяце опять вносим в счёт погашения тела кредита и т.д. А когда кредит закончится, а закроем мы его таким образом раньше, чем на 240 месяц, мы наши 11’010,86 рублей в месяц будем класть в депозит под процент pд.
Уж простите, но выводить аналитическую формулу для данной схемы мне было очень лень, поэтому ниже пойдут графики с результатами численных расчётов.
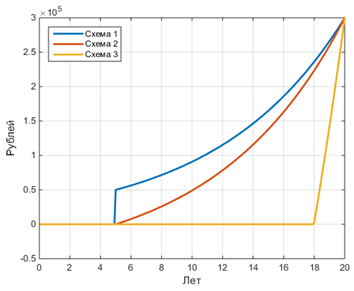
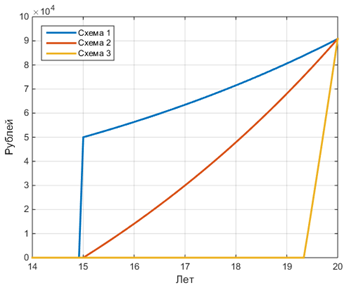
А пусть у нас будет ставка в банке по депозиту такая же, как и по кредиту. Знаю, что такого не бывает, а вдруг? Тогда график увеличения депозита по месяцам для трёх схем:
Интересно, да? Получается, что если ставка по депозиту и ставка по кредиту равны, то нет разницы гасить кредит досрочно или класть «лишние» деньги на депозит.
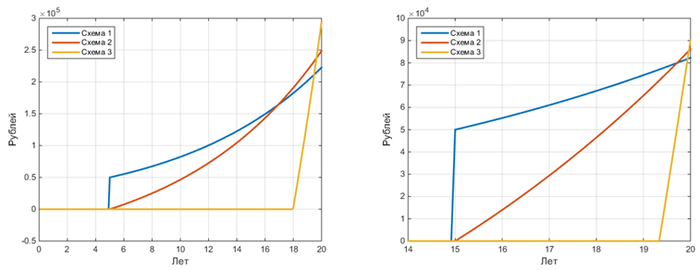
А что, если взнос делать на через 5 лет, а через 15? Результат для одинаковой ставки:
Масштаб по оси Х изменил, чтобы было лучше видно. Опять всё так же, как и в случае досрочного платежа в конце 5 года: к моменту конца кредита все три схемы дают одинаковый результат.
А теперь более реальный случай. Ставка по депозиту на 2% меньше ставки по кредиту (12% по кредиту и 10% годовых по депозиту). Результаты для досрочного платежа в конце 5 (60 месяц) и 15 (180 месяц) на левом и правом рисунках соответственно:
В обоих случаях с платежом в конце 5 года или 15 выигрывает схема 3, когда деньги дополнительно вносим в счёт погашения тела кредита до тех пор, пока не закроем его полностью, а потом начинаем откладывать ежемесячный платёж на депозит.
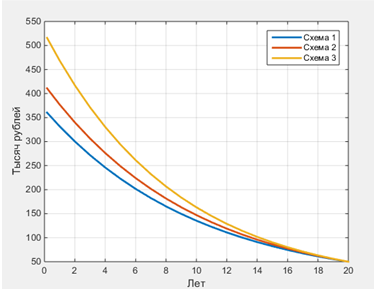
Конечно, чем раньше будет досрочный платёж, тем лучше. Для нашего варианта посчитал также экономию (а сэкономил – считай заработал!) в зависимости от момента внесения 50 тыс.:
Как видим, третья схема в любом случае самая выигрышная.
================================
================================
Выводы
Чтобы ни говорил в банке менеджер по кредитам или ваш знакомый, знайте, чем быстрее Вы закроете кредит, тем больше Вы сэкономите денег! Вкладывать деньги в депозит (облигации, ОФЗ и т.п.) стоит только в одном случае: когда ставка по депозиту выше ставки по кредиту! И это без учёта страховки жизни / недвижимости в течение срока кредита, которая тоже стоит денег!
Все умозаключения верны для условий РФ, где возможны досрочные платежи по ипотеке без дополнительных санкций и ограничений.
================================
================================