Как понять всё машинное обучение через линейную регрессию?
Сердце всех ML алгоритмов это функция потерь, научившись её оптимизировать мы поймём как обучаются машины.
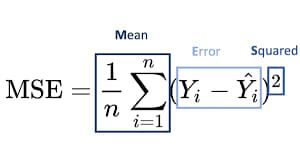
Дальше в посте, я опишу свойства функции среднеквадратичной ошибки (MSE), затем методы её оптимизации (аналитические, численные, стохастические и гибридные), укажу важные формулы, поведение градиента/Гессиана, оценки сходимости и практические рекомендации.
Основные свойства MSE
1. Дифференцируемость
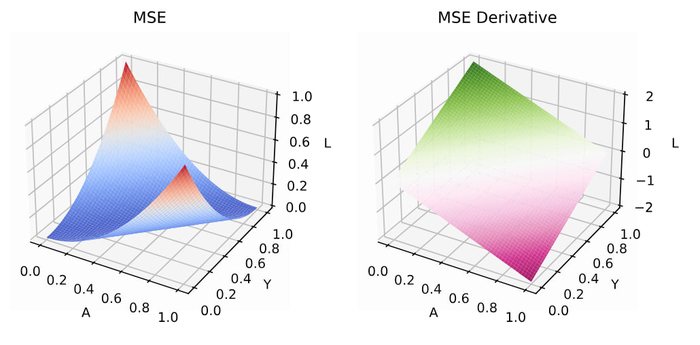
MSE — гладкая (бесконечно дифференцируема) функция параметров для линейной модели она квадратичная — что сильно упрощает анализ.
2 Квадратичность и выпуклость
MSE — квадратичная функция, такая функция выпукла (всегда), а если X⊤X положительно определена (то есть признаки линейно независимы и строго выпукла и имеет единственный глобальный минимум.
Для нелинейных параметрических моделей выпуклость обычно не выполняется — могут быть локальные минимума.
3. Градиент и Гессиан
Гессиан положительно полуопределён. Его собственные значения управляют «кривизной» функции (вдоль направлений с большими э-величинами функция круто меняется).
4 Шкала, чувствительность к выбросам и статистическая интерпретация
MSE сильно чувствительна к выбросам (квадратичная зависимость даёт большим ошибкам непропорционально большой вклад).
Если ошибки в модели нормальны, то MSE (максимизация правдоподобия) соответствует MLE — минимизация MSE = максимизация нормального правдоподобия.
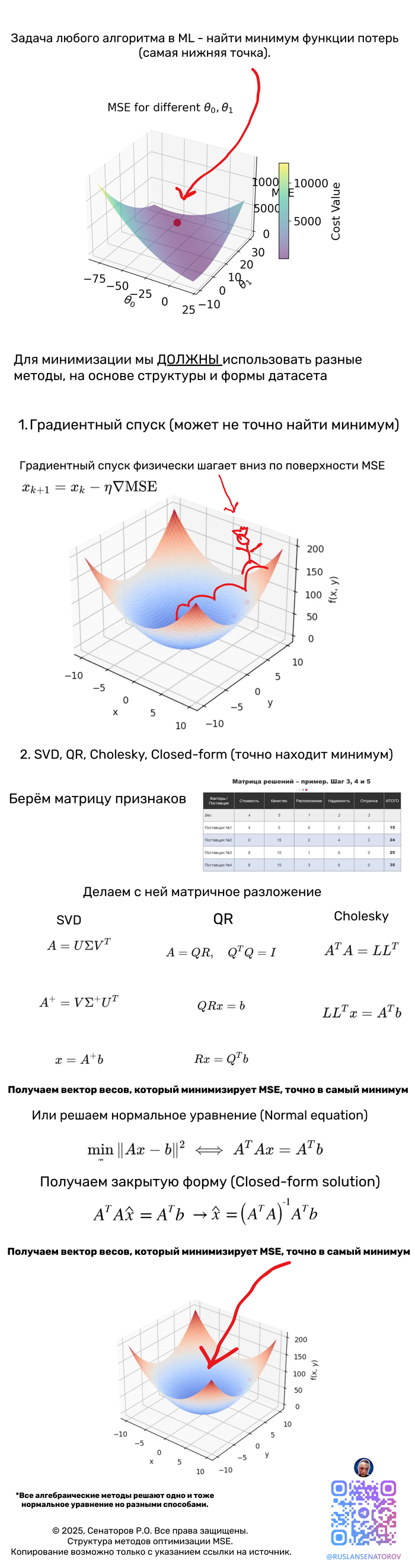
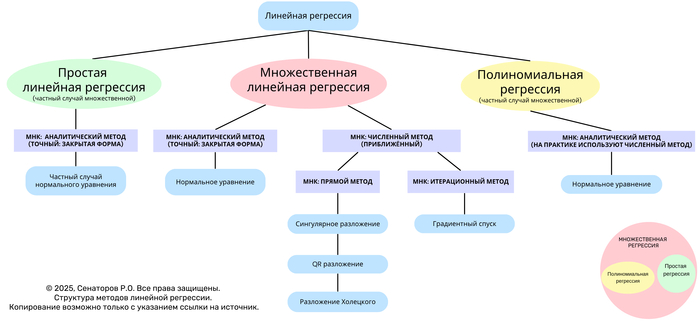
5. Аналитическое решение
Закрытая форма (normal equations).
6. Алгоритмы численной оптимизации
Градиентный спуск (Batch Gradient Descent)
7. Стохастический градиентный спуск (SGD) и мини-батчи
Стохастичность даёт возможность выйти из плохих локальных минимумов (для нелинейных задач).
8. Ускоренные и адаптивные методы
Momentum (classical momentum) — ускоряет спуск по узким долинам.
Nesterov Accelerated Gradient (NAG) — улучшенный momentum с теоретическими гарантиями.
Адаптивные алгоритмы: Adagrad, RMSProp, Adam, AdamW. Они подбирают адаптивный шаг для каждого параметра.
9. Второго порядка и квазиньютоновские методы
Newton’s method (использует Гессиан) Kвазиньютоновские: BFGS, L-BFGS Conjugate Gradient (CG) часто используют для ridge регрессии
10. Проксимальные и координатные методы (для регуляризации)
Coordinate Descent — особенно эффективен для L1-регуляризованных задач (LASSO), когда функция частично сепарабельна.
11. Прямые методы оптимизации
SVD, cholesky, QR
Обратите внимание что в посте вы не увидите саму модель линейной регресии, где мы точки прямой аппроксимируем, потому что это вообще неинтересно с точки зрения понимания моделей машинного обучения, интересно только сердце ML моделей - функция потерь.