Ответ на пост «Игры с повторениями»1
Исходник: Игры с повторениями
0) «... Реальные дуополисты не живут ровно одним решением, а принимают новые и новые решения день за днем. ...»
----
Вообще-то как раз нередко принимают стратегическое решение и далее пытаются просто продавить его силой, или просто тупо бьются как мухи об стекло не понимая есть их фантазии о реальности, а есть объективное столкновение с этой реальностью.
... Ловушка невозвратных затрат – одна из форм более широкого когнитивного искажения под названием «эскалация вовлеченности» ...
Но для таких людей как правило: «вся жизнь война», им не важнен результат, для них важней оказаться правым (даже если просто тупо смошенничал исковеркав «игру»).
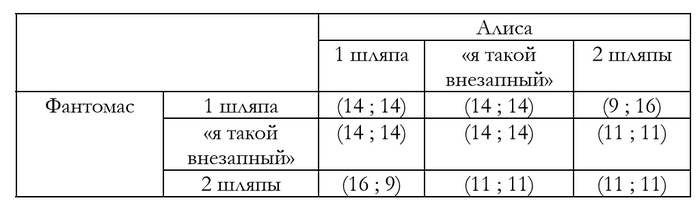
1) «... Третья стратегия – это делать одну шляпу до тех пор, как ваш противник делает то же самое, но переключится на две шляпы на следующий день после того, как ваш противник первым попытался на вас навариться. Если вы измените свою стратегию, то это потому, что ваш противник сам изменил ее, сделав две шляпы без предупреждения. ...»
---
Можно короче: принцип ведомого (отзеркаливание действий соперника).
Но у этой модели проблема в том что ты ведомый, т.е. реагируешь на ситуацию, а не задаёшь её исход.
2) «... Для однократной игры партнёрам стоит использовать принцип минимакса вне зависимости от того, содержит ли матрица платежей седловую точку или не содержит. Этот же принцип целесообразно использовать и при многократной игре с седловой точкой. ...»
---
Тут проблема в том что игрокам не всегда понятно когда игра разовая.
Вроде отжал «здесь и сейчас» по максимуму свою «львиную долю» пользуясь «правом силы», а игра оказалась в долгую (многократные игры).
И тут в игру вступает новая переменная «память о прошлых играх» (результаты предыдущих взаимодействий).
И оказывается что «никто не забыт, ничто не забыто» и тебе могут выставить «счёт» за прошлое. Аналогично и ты можешь «предъявить» «ты мне - я тебе». По сути с этого момента некооперативная игра начинает приобретать черты кооперативной, т.к. приходится учитывать интересы другого игрока, а не тупо «урвал побольше - убежал подальше», т.к. «куда ты денешься с подводной лодки?»© (мы в этой лодке до конца игры).
В пример см. Процессный подход и совершенствование с пункта «В».
3) «... Поэтому «чем случайнее, тем вернее», именно непредсказуемо случайное чередование стратегий не позволит добиться сопернику выигрыша. ...»
---
В реальности тут скорее начинается «картельный сговор». Игра из однократной превратилась а серию/цикл и чтоб её не порушить своей, или чужой жадностью и безрассудством приходится договариваться о внутренних правилах этой серии игр.
Вилке выигрышев в среднем и максимально для каждого в отдельно взятой игре (самоконтроль), допустимом давлении на оппонента и пр.
Но опять-таки это всё для формально равноправных участников. Если один из игроков (например фирма) думает что «я здесь власть) и купив трудовые услуги человека может его эксплуатировать. ... В реальности в договременоом сотрудничестве человек пользуясь «информационной асимметрией» https://ru.m.wikipedia.org/wiki/Асимметричность_информации (неявным знанием о работе для которой его наняли https://ru.m.wikipedia.org/wiki/Неявное_знание) будет восстанавливать социальную справедливость в меру своего понимания. В основе этой философии поведения лежит https://ru.m.wikipedia.org/wiki/Занавес_неведения и Некооперативные игры. Размышляя над «Ультиматумом» (мой комментарий по поводу игры «Ультиматум»).
4) Как писал чуть ранее неоднократность игры, её переход в серию + память о прошлых играх переводят эту «сериальную игру» в категорию кооперативных, в ином случае исходя из высших побуждений (справедливость) вечно проигрывающий игрок может из неё выйти и тем самым уничтожить оставив всех без выигрыша (см. игра «Ультиматум»).
Ага, я сейчас опять и снова про инновационную сферу и рационализаторскую деятельность.
Фирма считающая себя монополистом на местечковом рынке инноваций демпенгует через закупочные цены и роялти (авторские отчисления) на рацпредложения, изобретения, оптимизации и прочие инновации исходя из логики: «кому ты ткт ещё сможешь продать свои рацухи?, бери сколько заплатили».
Тем более что чиновники принимающие решения считают себя анонимным, организованным единством (говорящим от лица компании), а всех этих «Кулибиных» оголодавшими (финансирование из других источников) которые не умеют думать наперёд (просчитывая свою выгоду), которые не могут посмотреть историю прошлых игр для ретроспективного и проективного анализа инновационной игры чтоб понять какова будет их «гонорар успеха», или просто общаясь в своей среде поспрашивать у тех кто сыграл и сделал выводы уже Делёжка шкуры не убитого медведя (см. комментарии).
Как успехи?
См. https://ru.m.wikipedia.org/wiki/Индекс_глобальной_конкурентоспособности + https://ru.m.wikipedia.org/wiki/Интеллектуальный_капитал. В общем плохо, пока у нас игры «Царь Горы» и попытка урвать сиюминутно в псевдоразовой (однократной) игре, считая что тут игра с нулевой суммой, и готовые загрысть ради «победы». В других местах приоритет отдают долговременному, взаимовыгодному сотрудничеству (кооперативные игры) т.к. понимают что автор «гонорар успеха» потратит на себя в месте обитания, т.е. оставит деньги «на земле» и в экономике, а не законсервирует в золотом унитазе, часах стоимостью в элитную квартиру, океанскую яхту на которой бываешь 1~3 недели в год и прочий «дорого, пафосно и бесполезно».
Классическая https://ru.m.wikipedia.org/wiki/Игра_РП-РџР% где каждый сам за себя и сам по себе что и приводит к https://ru.m.wikipedia.org/wiki/Трагедия_антиобщин в виде проигрыша всех кто в этой «лодке». Ага, оказывается мы все по одну сторону, только на разных уровнях общества и государства, кто-то «как рабы на галерах», кто-то рулевой, кто-то просто разносчик чего-то там и вместо слаженной работы (кооперации) выясняем кто главный, кто-то себе строит плот из обшивки корабля (мне нужнее), кто-то топливо продаёт чтоб купить себе велосипед/трактор, кто-то паруса порезал на воздушный шар. В сумасшедшем доме попытка одиночного побега :-))) В общем, самовыживание без сотрудничества в основе которой «верхи не могут, низы не хотят» что и приводит к внутрикорпоративным войнам на истощение (в живых должен остаться только один).
По некоторым позициям обогнав нас в «эволюционной гонке» прогресса (НТР) на десятилетия (та же микроэлектроника, биоинженерия и пр. промышленное (а не лабораторное) производство).
«Гонка на дно» продолжается.