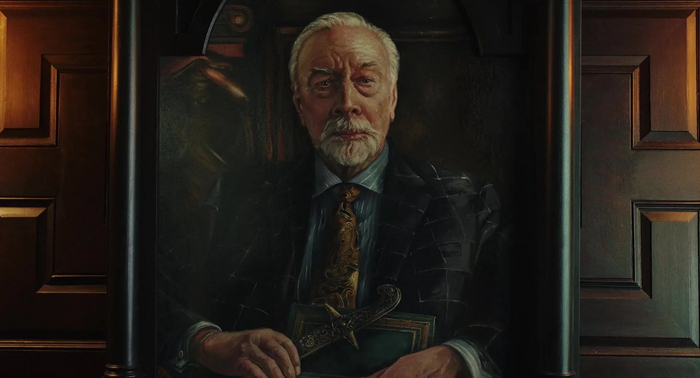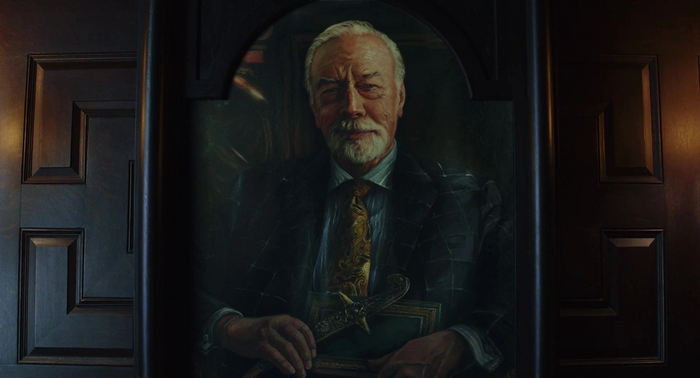Люблю детективы. Это почти всегда совмещение и просмотра фильма, и решение интеллектуальной загадки, которую создали авторы.
Причем с появлением кино, жанр детективов получил новое дыхание – можно расставить подсказки почти незаметно, не раскрывая разгадку раньше времени. Ровно настолько, чтобы подогревать интригу и интерес.
Идеальный пример такого детектива – “Достать ножи”, про чьи спрятанные детали я и расскажу в этом тексте.
Так, дисклеймер – предполагается, что вы посмотрели фильм, так как дальше будет куча спойлеров!
Портрет
Первое, что можно заметить при внимательном просмотре – это метаморфоза с картиной, изображающей главу семейства, писателя детективов Харлана Тромби (чью смерть и расследует детектив Бенуа Бланк).
Вначале фильма он изображен на портрете хмурым – ведь убийство еще не раскрыто!
Ну а в конце, после разгадки – мы видим довольную ухмылку.
Тут даже можно предложить объяснение – мы всегда видим картину глазами Марты. Сначала старик хмурится (так как она думает, что смерть Харлана наступила из-за ее ошибки).
Но когда все встает на свои места, и тайна разгадана – дед улыбается, одобряя детективный подход и словно прощая Марту.
Намеки на злодея
В фильме есть несколько ярких намеков на то, кто является злодеем.
В диалоге между Бенуа и Мартой, они упоминают, что собаки всегда хорошо понимают сущность людей.
А в самом начале нам вскользь сказали о том, что ночью лаяли собаки.
Ну и буквально в первом же появлении Рэнсома, где-то в середине фильма – собаки лают на него!
Нам опять показывают это вскользь, не акцентируя внимания.
Кстати, буквально через пару мгновений, Рэнсом скажет, что только прислуга зовет его Хью.
И это сыграет большую роль в дальнейшем.
Ведь когда Френ (экономка дома) умирает, она пытается назвать убийцу.
И сначала мы как будто бы слышим “You did this”
Но ведь Френ – экономка, то есть прислуга.
Которая как раз называет Рэнсома по имени – Хью!
Это и подтверждают нам в конце (даже субтитры видоизменили) – ведь слова Hugh и You очень созвучны, чтобы запутать и зрителей и Марту.
Небольшая, но симпатичная деталь – в доме у Рэнсома можно заметить отсутствующую бутыль на заднем плане
Ровно этой же бутылкой кто-то сжег лабораторию (где были результаты токсикологического отчёта Харлана)
Позже выясняется, что это был Рэнсом.
Ну и последний штрих – в разговоре с Мартой в самом начале фильма, Харлан прямым текстом говорит о том, что Рэнсом не может отличить бутафорский нож от настоящего
И в конце, герой Эванса подтвердит этот тезис буквально – попытается убить Марту с помощью ножа. Но по ошибке он схватит как раз бутафорский нож – перепутав с настоящим.
Про бейсбольный мяч
Моя любимая деталь (а точнее, почти самостоятельная линия) – это история бейсбольного мяча.
В самом начале фильма, мы видим, что Харлан обвиняет Ричарда (мужа дочери Харлана, Линды), в том, что знает про его измену.
Харлан угрожает отправить Линде письмо, со всеми деталями – если Ричард не признается сам.
После смерти Харлана, Ричард проникает в его кабинет, чтобы выкрасть письмо – но видит пустой лист.
Понимая, что старик блефовал, он, раздосадованный, выкидывает бейсбольный мяч в окно.
Там как раз мимо бредут детективы.
Бенуа Бланк, словно автоматически, подбирает мяч с земли.
Ближе к середине фильма, Бенуа играется с мячом, размышляя о загадке.
К нему прибегает собака и он кидает ей мячик.
Кстати, заметьте, как мастерски нам переключают внимание (чтобы отвлечь от путешествия мяча) – собака не просто так прибежала, она принесла важную улику, на которую сразу переключается Бланк (и мы вместе с ним, забывая про мячик)
Далее, на оглашении завещания, собака приносит мячик Линде – жене Ричарда, которой он изменяет.
И уже в самом конце фильма, Линда относит мяч на его место (стол отца), и видит там письмо, адресованное ей – как будто пустое.
Но оказывается, что у них была игра с папой, где они писали друг другу письма невидимыми чернилами.
Линда проявляет текст письма – и все узнает.
Вот так, иногда некоторым вещам нужно просто оставаться на месте.
Тут есть забавная точность с точки зрения бейсбольных правил – мячик кинул питчер (Харлан) на домашнюю базу. Бьющий (Ричард) отбил мяч (выкинул в окно), затем мячик прошел три базы (Бенуа, собаку и Линду) и вернулся обратно на домашнюю. Команда питчера (Харлана) – выиграла, Ричард (бьющий) – проиграл.
А еще мы могли догадаться, что письмо не пустое, еще до финала.
Линда упоминала, что у нее был своя игра с Харланом, в которую она играла.
И когда она показывала другие свои письма от отца, они были со следами ожогов – как раз от проявления невидимых чернил
Ну и как финальный штрих – обычно, невидимые чернила наносятся с помощью лимонного сока.
И что мы видим на столе у Харлана?
Конечно – вазу с лимонами!
“Достать ножи” – мастерски сделанный детектив.
Можно по разному относится к самой интриге и ее разгадке.
Но то, с каким трепетом и умом режиссер расставил подсказки, ввел второстепенные линии и развесил “чеховские ножи” – это точно достойно уважения.
Мой телеграм-канал (пост взят оттуда): https://t.me/odno_kino