Разработан гибридный метод, объединяющий траекторный подход MASH и теорию секулярного Редфилда для точного описания динамики открытых квантовых систем.
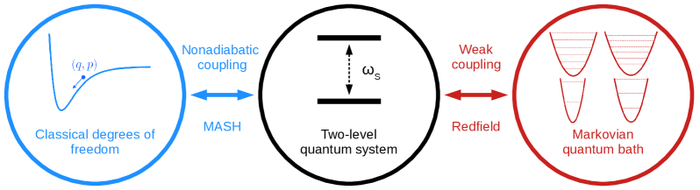
Гибридный метод Redfield–MASH позволяет исследовать взаимодействие двухуровневой квантовой системы с большим числом классических степеней свободы и марковским квантовым резервуаром, используя фреймворк MASH для обработки неадиабатической связи и секулярную теорию Redfield для описания связи с квантовым резервуаром.
В статье представлен метод, позволяющий эффективно моделировать неадиабатическую динамику в сложных молекулярных системах с классическими степенями свободы и квантовыми окружениями.
Моделирование динамики неадиабатических процессов в сложных молекулярных системах представляет собой вычислительную задачу из-за необходимости учета как квантовых, так и классических степеней свободы. В данной работе, 'Open quantum-classical systems: A hybrid MASH master equation', предложен гибридный подход, сочетающий траекторный метод MASH с секулярной теорией Редфилда для эффективного описания диссипативной динамики открытых квантовых систем. Разработанный метод позволяет моделировать взаимодействие квантового подсистемы с марковскими квантовыми резервуарами и немарковскими классическими степенями свободы. Возможно ли применение этого подхода для изучения более сложных процессов, таких как фотосинтез или спектроскопия в конденсированных средах?
Взаимодействие с Окружением: Основа Квантовой Динамики
Описание взаимодействия систем с окружающей средой – центральная задача квантовой химии и физики, сопряженная со значительными теоретическими трудностями. Традиционные подходы часто используют приближения, которые могут приводить к неточностям, особенно при сильном взаимодействии или длинных корреляциях. Точное описание этого взаимодействия критически важно для понимания передачи энергии, динамики реакций и декогеренции, требуя учета не только энергии, но и когерентности и корреляций. Эффективное моделирование требует баланса между точностью и вычислительными затратами, а каждая оптимизация должна тщательно анализироваться, чтобы не нарушить фундаментальные принципы взаимодействия.
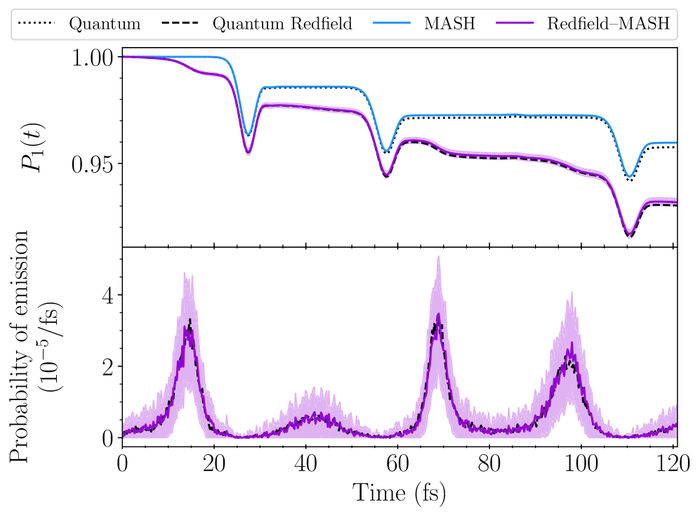
Исследование динамики заселения верхнего адиабатического состояния показало, что для изолированной системы квантовые и MASH-вычисления дают схожие результаты, в то время как результаты квантового Redfield и гибридного Redfield–MASH методов для связанной системы–полости демонстрируют влияние взаимодействия с полостью, при этом погрешность, оцениваемая как 95% доверительный интервал для 10⁵ траекторий гибридного метода, отображается в виде полос погрешностей.
Гибридные Подходы: Мост Между Квантовым и Классическим Мирами
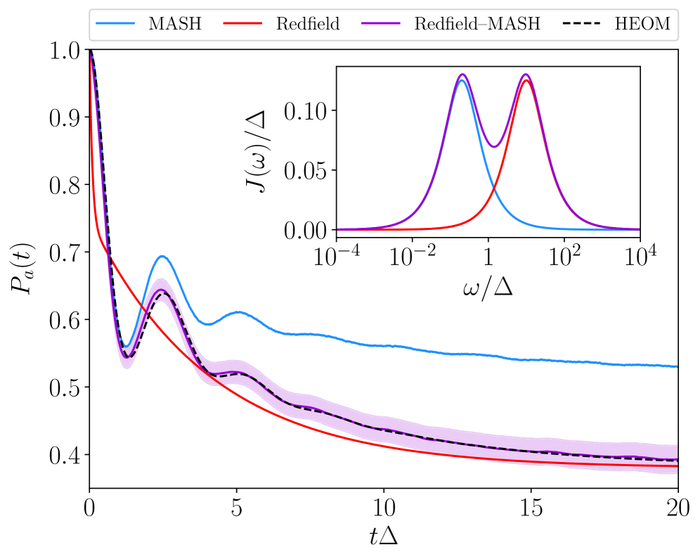
Метод "Гибридный Redfield-MASH" – эффективное решение для моделирования открытых квантовых систем, сочетающее преимущества классических траекторных методов и квантово-механических формализмов. Он позволяет преодолеть ограничения стандартных методов, описывая классические степени свободы явно, а квантовые ванны – с помощью теории Редфилда. Метод использует разделение временных масштабов для детального рассмотрения как быстрых, так и медленных процессов, при этом вычислительные затраты сопоставимы с методом MASH. Точность метода подтверждена сравнением с более ресурсоемким методом HEOM.
Сравнение динамики заселения диабатического состояния |a⟩, полученной методами MASH, секулярной теории Redfield, гибридным Redfield–MASH и HEOM, показало, что гибридный метод обеспечивает наилучшее соответствие результатам HEOM, при этом погрешность, оцениваемая как 95% доверительный интервал для 10⁴ траекторий гибридного метода, отображается в виде полос погрешностей, а вклад в спектральную плотность от медленной (синий), быстрой (красный) ванн и общей спектральной плотности спин-бозонной системы (фиолетовый) представлен на вставке.
Уравнение Главного Уравнения и Гибридная Структура: Основа Точного Моделирования
Уравнение Линдблада предоставляет математически строгую основу для описания динамики открытых квантовых систем, гарантируя положительную определенность матрицы плотности. Для упрощения численного решения часто используется секулярное приближение, удаляющее быстро осциллирующие члены и обеспечивающее численную стабильность. Комбинирование подходов на основе уравнения главного уравнения и гибридной структуры позволяет обеспечить согласованное и точное описание диссипации и декогеренции, демонстрируя качественное соответствие результатам, полученным с использованием точной формальной интегральной теории HEOM.
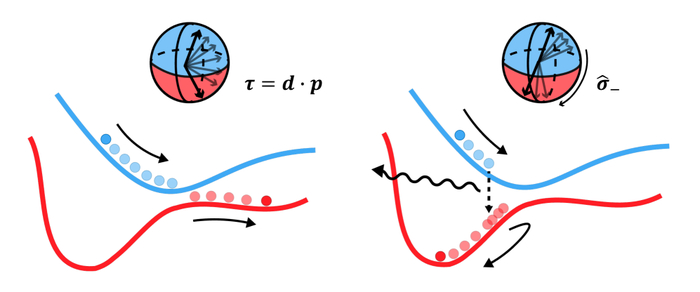
Гибридный метод демонстрирует два различных механизма изменения активного состояния: энергосберегающие неадиабатические «переходы», опосредованные связью с классическими координатами при прохождении спин-вектора через плоскость экватора, и стохастические «скачки», инициированные операторами Линдблада, связывающими систему с квантовой ванной.
Неадиабатические Эффекты: Взгляд за Грань Традиционной Динамики
Моделирование неадиабатических процессов, при которых системы переходят между электронными состояниями, требует особого подхода. Традиционные методы, такие как 'Surface Hopping', могут сталкиваться с проблемами сохранения энергии или искусственным затуханием. Взаимодействие между неадиабатической связью и влиянием окружающей среды может приводить к неожиданной динамике, подчеркивая необходимость комплексных симуляций, учитывающих все значимые факторы. Подобно хрупкому равновесию живого организма, устойчивость системы в неадиабатических процессах рождается из ясного понимания связей и границ.
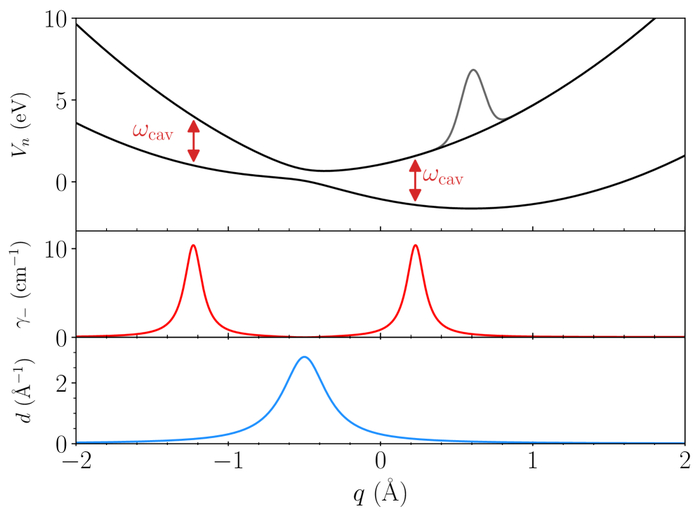
Анализ адиабатических потенциалов, представленных в уравнении (36), и соответствующих скоростей затухания, усиленных полостью, а также неадиабатических связей показал, что при резонансе с полостью наблюдается энергетическая щель, обозначенная красными стрелками, а начальный волновой пакет представлен серым цветом.
Данная работа демонстрирует стремление к созданию элегантной модели для описания динамики открытых квантово-классических систем. Подход, сочетающий MASH и секулярную теорию Редфилда, позволяет учитывать влияние как квантовых, так и классических степеней свободы, что особенно важно при моделировании сложных молекулярных систем. Как однажды заметил Пол Дирак: «Я не понимаю, почему люди так неохотно принимают простую идею, что вся материя состоит из квантов энергии». Эта фраза отражает суть представленного исследования – стремление к упрощению сложного, выделению фундаментальных принципов, определяющих поведение системы. В данном случае, структура взаимодействия квантовых и классических элементов определяет динамику всей системы, что подтверждает важность целостного подхода к моделированию.
Что впереди?
Представленная работа, подобно тщательно спроектированному городскому району, демонстрирует возможность согласованного развития квантово-классических моделей. Однако, даже самая элегантная инфраструктура не избавляет от необходимости дальнейшего планирования. Существующие подходы, включая описанный гибрид MASH и секулярной теории Редфилда, всё ещё испытывают трудности при масштабировании на системы с большим числом классических степеней свободы и сложными квантовыми окружениями. Очевидным шагом представляется разработка алгоритмов, позволяющих эффективно отслеживать корреляции между классическими и квантовыми подсистемами, избегая экспоненциального роста вычислительной сложности.
В перспективе, представляется важным отойти от концепции жесткого разделения на квантовые и классические подсистемы. Более реалистичные модели должны учитывать когерентные эффекты, возникающие на границе между этими мирами. Необходимо исследовать возможности адаптации методов, разработанных для описания открытых квантовых систем, к задачам, где классические степени свободы играют доминирующую роль. Упрощение, подобно удалению лишних деталей из сложного механизма, должно служить не упрощением понимания, а углублением.
В конечном итоге, успех этого направления будет зависеть не только от развития вычислительных методов, но и от более глубокого понимания фундаментальных принципов, определяющих динамику открытых квантово-классических систем. Прогресс, как известно, не является линейным; он требует постоянного переосмысления и готовности к неожиданным открытиям. Иначе говоря, система должна эволюционировать, а не перестраиваться.