Доброго всем времени суток, продолжаю серию постов про образовательную робототехнику. Здесь я описываю результаты и просто ход выполнения своей научной работы.

Кратко: разрабатываю специальную робо-накидку на одежду, которая сможет оцифровывать часть двигательных навыков мастеров своего дела и передавать это тем, кто только учится.

О чем этот пост: "сырые" данные, полученные с МЭМС гироскопов и акселерометров нужно во-первых преобразовать в углы, а во-вторых необходимо максимально избавиться от зашумленности. В этом посте покажу эффективность разных подходов при помощи такой штуки как вариация (или дисперсия) Аллана.

Цель: получить основу для сравнения существующих решений с моими предложениями по корректировки ошибок на сенсорах. Необходимо использовать зарекомендовавшую себя систему оценки. Из разряда было - стало.

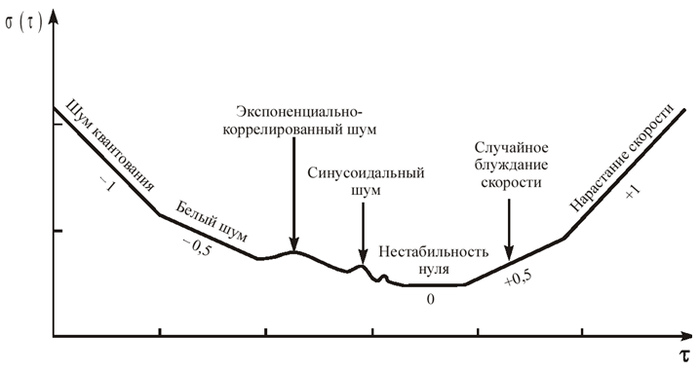
Как будем делать? Да очень просто. Вариация Аллана используется для оценки стабильности измерений генераторов. Например, можно оценить погрешности для работы часов. Стоп, а причем тут тогда твои сенсоры? Дело в том, что если положить сенсоры и не трогать их, то в идеале все 6 осей должны выдавать одинаковые значения (так конечно не будет в реальности). Например, для осей гироскопа это должны быть нули, а для акселерометра - проекция на вектор силы тяжести. Так же сама оценка очень наглядно показывает уровень погрешности во времени. Примерно так.

На разных масштабах усредняем дисперсию. Выводим графики в логарифмическом виде и получим нечто подобное. На питоне есть хорошая реализация вот тут

Теперь все готово, чтобы начать. Берем наши любимые сенсоры. Запускаем сбор сырых данных на 6 часов с частотой около 50 Гц. Так же записываем время получения данных (сколько времени прошло с момента запуска микроконтроллера). Получается небольшой датасет ~80мб.

av - уровень дисперсии

tau - временное окно усреднения

Можно заметить, что какое-то время данные за счет усреднения избавляются сами собой от ошибок. Ошибка достаточно большая даже для минимального значения. И раз уж мы заговорили про усреднее, то может добавим немного алгоритма плавающей средней? Это когда вместо самого значения мы усредняем три последних и записываем его. Посмотрим для случае, когда усредняем 3 последних значения.

Картина стала на один порядок лучше для значений до 100 мс. Хорошо это или плохо? Давайте посмотрим далее на окно в 17 соседских значений.

Вроде бы стало поменьше в начале, но появилась большая инертность при появлении новых значений. Да и общая картина не поменялась. Попробуем взять теперь альфа-бета фильтр.

Для данных отдельно в начале посчитал оптимальные значения альфа и бета. Уже получше выглядит. Но общий ландшафт не меняется. На этом моменте уже подумал, что и дальше буду получать подобные картины. Идем далее, фильтр Маджвика. Один из популярных алгоритмов для получения углов ориентации. Будем использовать версию без магнитометра.

Вот это уже повеселее! Если посмотреть на вертикальную ось, то можно заметить порядок ошибок с минусовыми степенями. Это прям вообще хорошо. Но в связи с этим слайдом возникают вопросы:

1) Не связано ли это просто со сменой формата представления данных? В первых случая мы имели дело с сырыми целочисленными значениями. Для акселерометра значения проекции могут и за 3000 спокойно выходить, а тут все значения до единицы и тип float.

2) Все ли преобразованные в углы данные имеют такой порядок и набор ошибок?

Сейчас узнаем.

Встречайте, царь-фильтр. Фильтр Калмана.

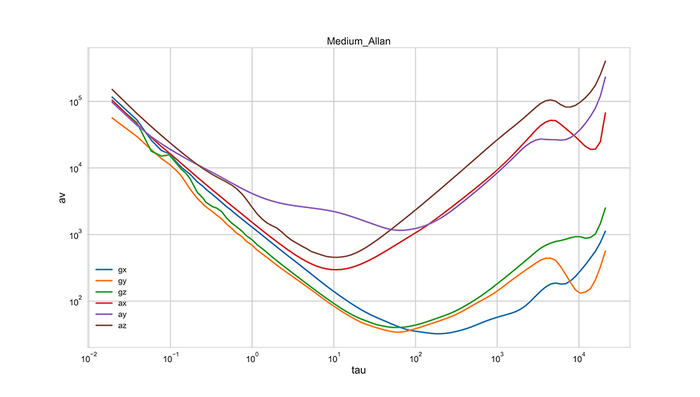
Были использованы только сырые данные без преобразования в углы. Предварительно сделал небольшую сетку для поиска оптимальных параметров. Как видите, практически нет спуска слева направо. А это значит ошибки дискретности нет. Но и цена производительности большая. На 2.2 миллиона значений я потратил около 6 часов времени, против получаса у Маджвика. Красота да и только.

Теперь ответим на второй вопрос. Углы можно получить только по гироскопу простым интегрированием. Давайте посмотрим.

Такая же прямая... НО!... Посмотрите ка на вертикальную ось. Это Вам не яйца в профиль. Это 9 (девять, ДЕВЯТЬ!!11) порядков разницы. UDP: сами графики не правильно подписал, там должны быть углы поворота вокруг оси x, y, z просто.

Раз уж мы поговорили про расчет только по гироскопу, так давайте посчитаем только по акселерометру! Ух, гулять так гулять. Кстати там только для двух осей будут данные. Почему так - мне не сказать лучше, чем это сделали до меня:

Третья ось полезна для определения отклонения от оси центра тяжести (в покое), ну и все. Для вращения нужен строго гироскоп.

Эта зараза хоть и подвержена сильной реакции на вибрации. Но посмотрите на порядок ошибок! Загляденье. Для инертных систем просто шикарно.

Далее я смотрел комплементарный фильтр первого порядка, но там ничего особенного. Скучный график не вносящий ничего нового. Помимо этого пробовал пошалить и применить к фильтру другой фильтр (хотя смысла в этом не сильно много). Зато узнал, что ели в начале применить фильтр Калмана, а потом Маджвика, то начальная ошибка порядка 10 в минус 13, а если поменять порядок, то будет уже 10 в минус 15. Вот так вот.

Был рассмотрен самый примитивный случай покоя. Далее буду готовить парные данные. Когда буду одновременно собирать данные с моей перчатки и с Leap Motion. Камера будет в качестве опорной базы. Получится, что данные 100% имеют одну природу. Поэтому в идеальном мире если вычесть из опорных данных мои, то должны быть идеальные нули. Так конечно не будет, но это хороший метод выравнивания данных, чтобы сказать что они как-будто однородные. И на этом можно снова оценить степень ошибки с помощью вариации Аллана.

Если говорить глобально, то никаких новых результатов тут нет. Лишь очередной раз показал, что Калман крутой и дорогой, Маджвик хорошо и быстр, интегрирование в чистом виде - зло, плавающая средняя - успокоения, мол я пытался. И это хорошо, что результаты по графикам согласовываются с мировыми выводами. Значит это хорошая платформа для оценки погрешностей МЭМС сенсоров.

По всем рассказанным алгоритмам есть собранные датасеты. Если хотите поиграться, то оригинальные сырые данные можно скачать по ссылке выше. Обработанные данные могу дать по запросу.