#19 | Капуста Романеско заставляет вспомнить что-то очень фундаментальное |
Минутка универсальных паттернов.
Каждый раз, когда я смотрю на фрактальную капусту Романеско, меня посещает мысль: это не капуста такая особая и удивительная, это принцип фрактальности таков, универсальный и завораживающий, а капуста лишь по каким-то одной ей ведомым причинам выступает хорошим визуальным проводником этого вселенского принципа, выводит его в свет из непроявленного.
И самое интересное то, что есть все основания предположить: раз оно в капусте проявлено (из известных других примеров — снежинки, кораллы, грозовые молнии, дельты и русла рек, кровеносная система, лист папоротника, крона и ветви дерева, листья и прожилки на листьях), значит оно ещё много где проявлено (или может быть проявлено), и не обязательно в визуальной плоскости — это могут быть также сюжетные, смысловые, образные и многие другие "невизуальные" измерения фрактальности.
Далеко за примером ходить не придется — "мономиф" путешествия героя в сказках, мифах и легендах.
***
Если тебе, добрый читатель, понравилась эта заметка, не забудь, пожалуйста, поставить великодушный лайк и подписаться. Ещё больше полезной и обжигающей рецепторы годноты будет в моей уютной тележеньке: SOLA|ZEN
Множество Мандельброта
Я сам делаю множество Мандельброта. Это какой фрагмент из БЕСКОНЕЧНО! То есть пусть в другом веке в совсем другой галактике. Пусть он трехногий! А множество ОДИНАКОВОЕ! Оно минует абсолютно все! Все миллиардов световых лет.
Трёхмерная бесконечность: мандельбульб и его замысловатые узоры
Мандельбульб — это трёхмерный фрактал, который представляет собой своего рода обобщение знаменитого множества Мандельброта, но в трёхмерном пространстве. В отличие от классического множества Мандельброта, которое строится в двумерной плоскости комплексных чисел, каноническое трёхмерное множество Мандельброта создать невозможно, так как не существует полноценного аналога комплексных чисел в трёх измерениях. Однако мандельбульб удалось сконструировать, используя кватернионы и бикомплексные числа, которые позволяют работать в четырёхмерном пространстве. Впервые идею такого фрактала предложил Жюль Рюис в 1997 году, а в 2009 году Даниэль Уайт и Пол Ниландер усовершенствовали её, применив сферические координаты. Они разработали формулу, в которой вектор возводится в степень n, обычно равную 8, что создаёт характерную форму мандельбульба — объёмную, похожую на шар структуру с ломаными, повторяющимися деталями на поверхности, напоминающими ветви или лопасти. Число этих «лопастей» зависит от выбранной степени n, и при увеличении степени фрактал становится всё более сложным. Мандельбульб обладает бесконечной детализацией: при увеличении изображения открываются всё новые и новые узоры, как и в двумерном множестве Мандельброта. Однако, несмотря на визуальную красоту и сложность, математики до сих пор спорят, является ли мандельбульб истинным трёхмерным аналогом множества Мандельброта, так как некоторые его участки менее детализированы, чем ожидалось.
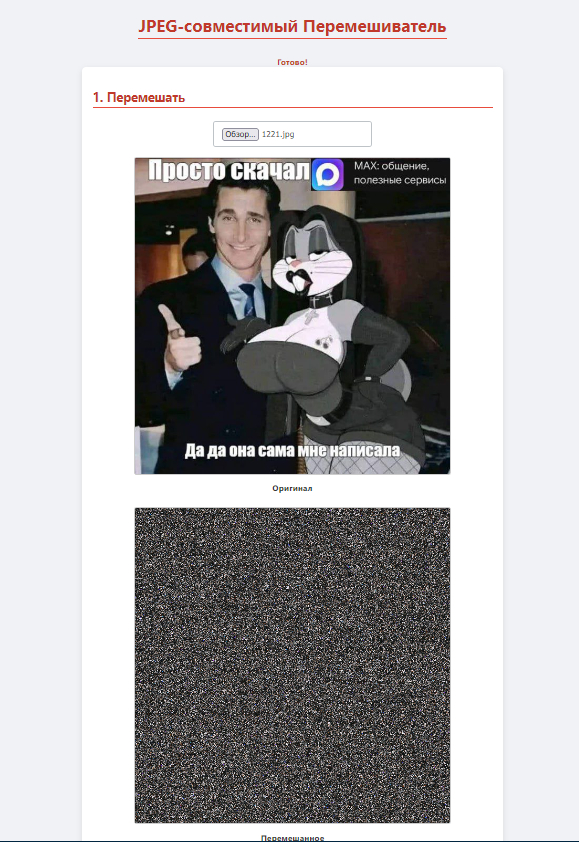
Ответ на пост «Шифровальщик картинок (с использованием Perfect Shuffle). Чтобы мамка не заругала»1
Онлайн реализация шифровальщика - дешифровальщика JPEG
Пиксели перемешиваются. По алгоритму обратимо. И это Постить можно на любых форумах.
При востановлении тональность немного меняется.
Про шифрование картинок и стеганографии известно давно, но онлайн реализаций этого нет.
Исходный код открыт, онлайн реализация.
https://codepen.io/procoders000001/full/qEOEgNe
( код работает локально без доступа к интернету )
Если сайт жмёт сильно разрешение есть риск что изображение не востановится.
Ого, а что тут?
А тут?