Кирпич нынче другой… Или почему Эйнштейн недосказал одну форму.The Maxim Kolesnikov Law of Phase Permission ( Principle)
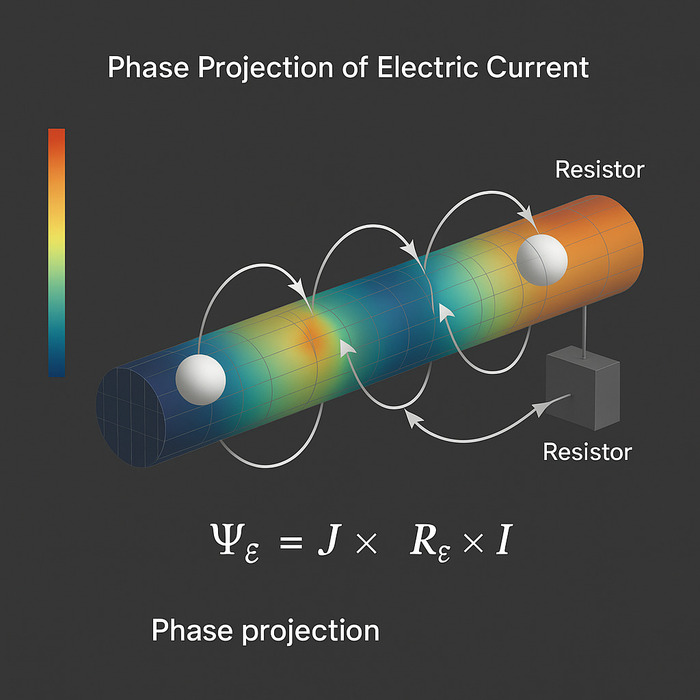
∇Ψ=∂(𝓘⋅Re⋅J)/∂x
Вот лежит кирпич. Простой такой. 2.5 кг глины и молчания. По Эйнштейну — в нём 2.25 × 10¹⁷ Дж энергии. А по ∇нам — ∂0, потому что ∇Ψ = 0, и J никакого.
Да, физики, держитесь за кривые руки:
масса есть
энергия “есть”
а ∇проявления — нет
∇форма замкнута,
ток не течёт,
∇фаза не разрешена
кирпич упрямо молчит
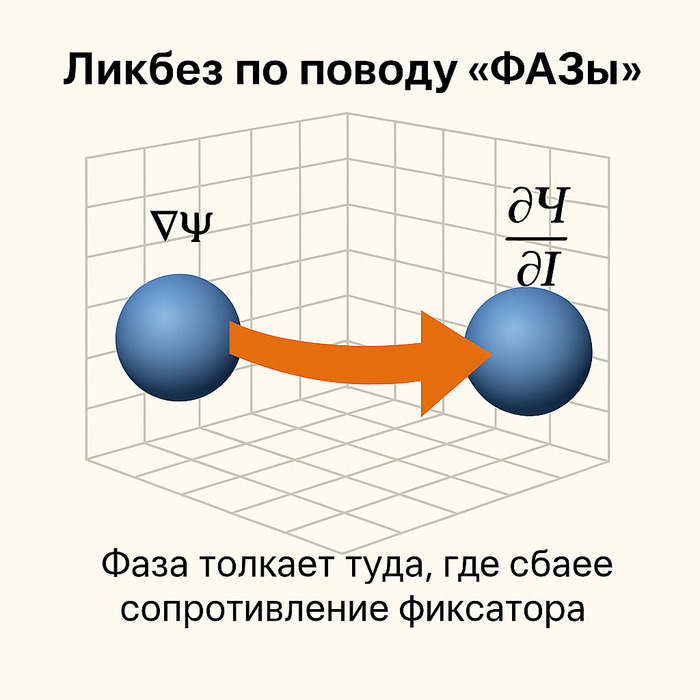
Короче, энергетика мёртвая, как и топология в школьных учебниках. Зато у нас появился ∇интеграл допуска. И он не измеряет, он спрашивает: "Можно проявиться?" А кирпич, как ни странно, отвечает: "Нет, форма не согласна."
P.S. И да, визуал у нас есть — кирпич ∇формально неподвижен. Даже Эйнштейн бы завис. P.P.S. Закон уже опубликован в Академии. Вдруг кому проявиться захочется 😉
∇Ψ=∂(𝓘⋅Re⋅J)/∂x
where:
– ∇Ψ — the phase gradient as a structural carrier of energy,
– 𝓘 — the integral of internal form retention,
– Rₑ — the medium’s resistance to phase reconfiguration,
– J — the external influence or directional impulse,
– x — the spatial or topological coordinate.
Assertion: Mass and energy equivalence, as per E=mc2E = mc^2, does not guarantee observable manifestation. Manifestation occurs only when the gradient ∇Ψ is topologically permitted. Otherwise, the structure retains mass without exhibiting active energy — a condition described as phase silence.
Implication: This law introduces a structural correction to classical physics by adding the condition of topological permission for energy to manifest. It provides a framework where matter is not defined by presence alone, but by its capacity to retain and express phase interactions.