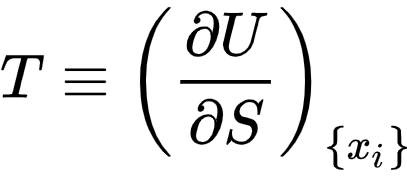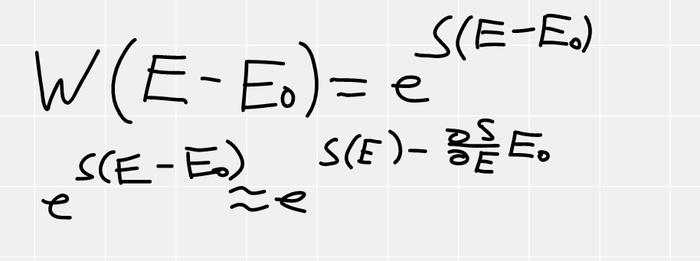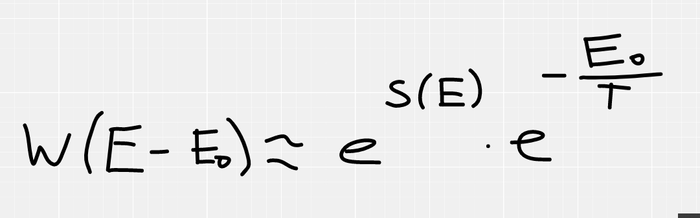Прошу помощи-совета у гуру сантехники
Очень прошу совета от опытных сантехников, гуру термодинамики. Ситуация следующая:
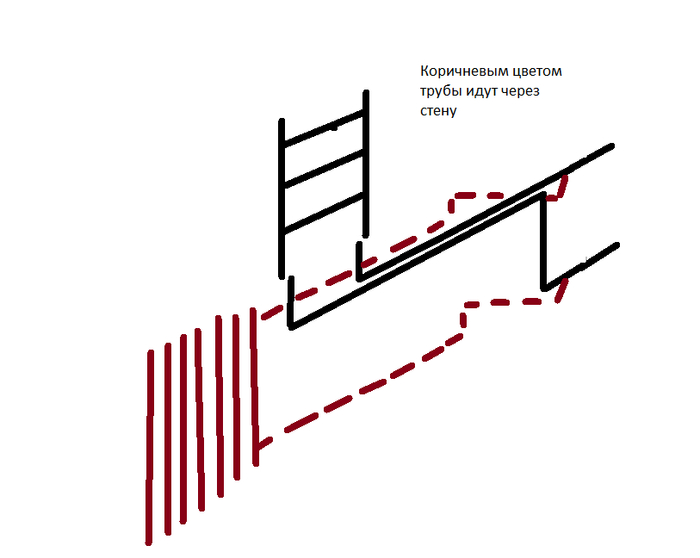
От однотрубной системы отопления (санузел, для полотенчика) сделали ответвление в кладовку. Результат - батарея не греет, полотенчик греет. Возможности изменить трубы черным цветом нет, как и само разветвление. С коричневыми можно "играться". Материал труб - ПП20. Батареи биметал, 7 колен. Возможно ли что то исправить?
П.С. Схему реализовывал наемный сантехник, поэтому не судите. Сейчас с этим всем пробую сам разобраться, его уже не затянуть.
Энтропия и стрела времени
Что такое энтропия? В каких областях она используется? И как она объясняет направление, в котором происходят преобразования? Об этом в видео от ScienceClic
Температура, что это?
В своём прошлом посте я остановился на том, что о температуре как физической величине, люди мало что знают. В школе так вообще отделываются лишь "мерой движения молекул" и на этом заканчивают. А ведь это довольно любопытная штука, смысл которой далеко за простой "средней энергией частиц". Давайте попробуем разобраться, что про неё известно и какие определения температуры есть, и можно ли как-то например дать температуру одной молекуле.
Если копаться всерьез, то очень больно для головы. Потому что количество определений для температуры слишком большое. У разных разделов физики порой разные определения, так и даже в самой термодинамике есть куча вариантов аксиоматики. На одной вики их штук 10, если копать научные статьи, то вполне можно еще десяток другой вариантов найти. Мы не полезем в эти дебри и разберем лишь два определения, первое из классической термодинамики, второе из статистической физики (в которой становится понятнее, как всё же её пощупать можно).
Если грубо разделить аксиомы классической термодинамики на две группы, то в одних аксиоматических построениях температуру просто постулируют как некую физическую величину, которая просто есть (неопределяемая переменная), является интенсивной величиной и количественно выражает интуитивное понятие о различной степени нагретости тел. В других построениях, как неопределяемую базовую переменную вводят энтропию, а температуру определяют как частную производную энергии от энтропии.
Хоть эта запись и пугает всех, кто не знаком с курсом математического анализа, на человеческом языке, она означает "температура это скорость роста энергии при росте энтропии, при неизменном объеме, массе веществ, площади поверхностей и т.д."
Отлично, а что там в статистической физике? Ну условно, там та же формула, что и на картинке выше. Но лучше показать на простейшем примере.
Для примера я возьму систему с десятью монетками. Давайте договоримся, что если монетка орлом вверх, то она имеет энергию 0, если решкой вверх, то энергия такой монетки будет у нас 1.
У системы на картинке энергия 2. У системы с десятью орлами, энергия будет 0. В прошлом посте я объяснял, как считают энтропию в статистике. Так что давайте посчитаем сколько микросостояний дает нам разную энергию.
E = 0 можно получить имея все монетки орлом вверх, это одно состояние, энтропия 0.
E = 1 можно получить имея одну решку, она может быть на первом, втором... и т.д. месте, микросостояний 10, энтропия k*ln10
E = 2 еще больше вариантов, их 45, а энтропия k*ln45
E = 3, вариантов 120, энтропия k*ln120
и т.д.
Реальные физические системы с таким простым набором состояний существуют, например система спинов в магнитном поле: типичная начинка квантового компьютера, атомы водорода в ЯМР спектрометре или они же в томографе.
У обычных больших тел (стакан воды, суп на плите, пробирка) квантовых состояний в невероятное количество раз больше, но с ростом энергии количество возможных вариантов аналогично растет, функцию E(S) можно вполне себе считать непрерывной. Для макрообъектов расстояние между уровнями энергии настолько мало, они так сгущаются, что измерить этот зазор невозможно даже в теории. Энтропию можно ввести и через классическую механику, рассматривая молекулы как шарики, правда там немного иначе она будет считаться, но ответ совпадает с квантовым рассмотрением.
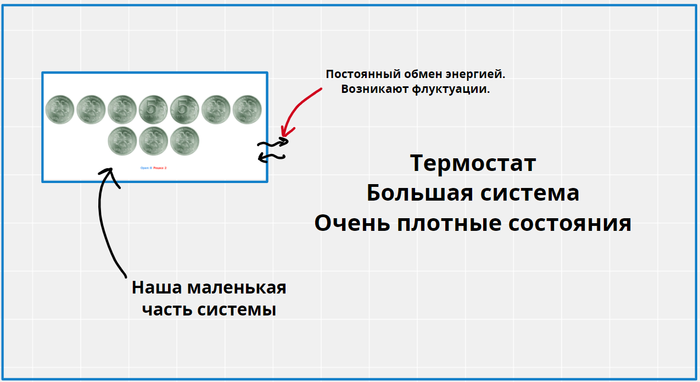
Внимательные наверное уже заметили, что в определении температуры формула содержит производную, а в примере у меня дискретная функция, у которой нельзя посчитать производную. Именно так, понятие температуры в строгом смысле работает только для макроскопических объектов с кучей уровней, где мы не можем заметить, что функция E(S) дискретная. Для описания температуры объектов с малым количеством уровней, приходится сначала утверждать, что такая система находится в состоянии термического равновесия с термостатом (модельная среда, с конкретной температурой), но тогда наша система уже не имеет конкретную энергию, и имеет лишь вероятности находиться на том или ином уровне, ведь между маленькой системой и большим термостатом возникают флуктуации. Эти вероятности легко посчитать, пользуясь нашими формулами. Собственно для маленьких систем, температура уже будет иметь немного другой смысл, и быть скорее параметром, который описывает распределение вероятностей по уровням. О как!
Возьмем всё ту же систему с монетками, и попробуем выяснить как температура окружающей среды будет влиять на её энергию. Представим, что она находится в равновесии и контакте с какой-то другой системой, огромной по сравнению с ней, но при этом конечной.
Всё вместе мы представим изолированной системой с энергией E. Попробуем найти вероятность быть нашей системе в каком-нибудь состоянии с энергией E0.
У нас вся система, обладает каким-то набором микросостояний, пусть их W штук. Нам просто нужно найти сколько из них, подходят нам и поделить это число на общее количество.
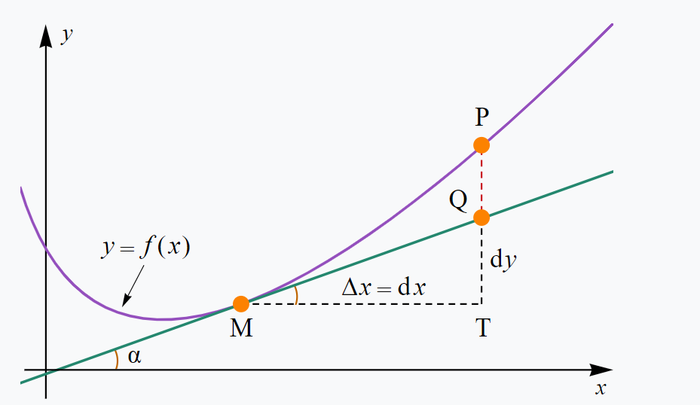
Если наша подсистема, в состоянии с энергией E0, то на термостат остается E-E0. Учитывая, что W=exp(S), получаем, что вероятность пропорциональна exp(S(E-E0)), но как это посчитать? Мы не зря посчитали, что термостат НАМНОГО больше чем наша подсистема, поэтому E0<<<E, а значит мы можем воспользоваться приближенным вычислением (в данном случае оно оказывается точным) с помощью производной. Рядом с точкой M, функция почти не отличается от своей касательной, в этом смысл дифференциала и производной.
Во всем выводе я убрал константу Больцмана, считайте, что я принял её единичкой, это не так важно.
В формуле появилась производная энтропии от энергии (что есть 1/T по определению из начала поста). И в конце концов мы получаем
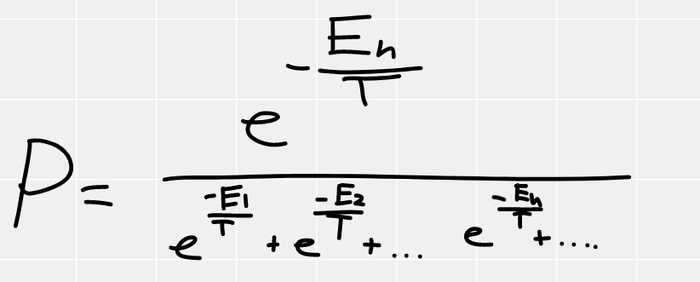
Вероятность должна быть пропорциональна W, при этом в сумме они все должны давать единичку, поэтому вероятность нашей маленькой системке находиться в n-ом состоянии (у которого энергия En), будет
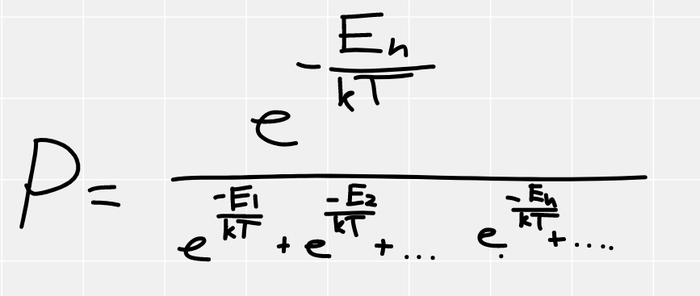
Если вернуть везде постоянную Больцмана, получится так
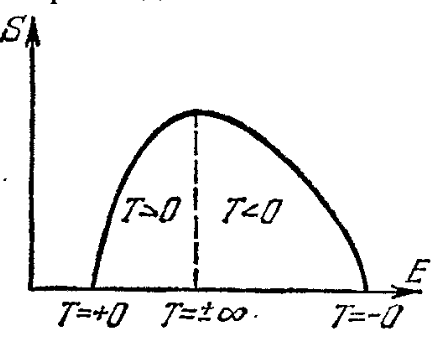
Снизу в формулах энергии всех остальных уровней. Очень симпатичная формула, называется распределением Гиббса. Из неё можно вывести распределения Максвелла, Больцмана и прочие прекрасные частные случаи. По ней видно, что если температура абсолютный ноль, то система находится в низшем состоянии с вероятностью 1, если же температура бесконечна, то система равновероятно может находиться во всех состояниях от низшего до наивысшего, что немного контринтуитивно (кажется, что бесконечная температура, это наивысшее состояние по энергии), но как видите это не так. Температура это сложный статистический параметр, а не просто энергия тела как нам кажется интуитивно.
Еще один интересный вывод из такой формулы вытекает если наша система имеет конечное количество состояний (как наш пример с монетками имеет всего 1024 состояний, и 10 уровней), то возможно представить себе отрицательную температуру. Это состояние будет отвечать энергии системы даже большей чем, энергия системы при бесконечной температуре, ибо высшие уровни заселены чаще чем низшие (при бесконечной они поровну все заселены). Мы можем создать искусственно такие состояния в реальности, ведь системы с ограниченным количеством уровней существуют, а способы "перевернуть заселенность" существуют.
Но откуда же у нас всех берется знание, что температура отвечает за скорость молекул? А дело в том, что если мы применим распределение Гиббса к идеальному газу, то средняя кинетическая энергия молекулы будет 3/2kT, об этом нам рассказывают в школе сразу в готовом виде (исторически температуру с этого случая вводили и в науке), и на этом же эту тему заканчивают, отсюда и остается подобный обрубок понимания довольно сложного понятия температуры.
Учитывая, что статистическая физика и термодинамика стоят на очень простых принципах из математики, выходит довольно любопытная ситуация. Дело в том, что и общая теория относительности, и квантовая механика отлично стыкуются с термодинамикой. Но как мы знаем, между собой ОТО и КМ очень плохо стыкуются, и квантовую теорию гравитации до сих пор не разработали. Так же мы знаем, что внутренности и поверхности черных дыр, обладая страшной кривизной пространства-времени, должны описываться той самой пока несуществующей квантовой теорией гравитации, но мы точно понимаем, что эта теория должна тоже хорошо стыковаться с термодинамикой. Изучение термодинамики черных дыр сразу показало, что они должны обладать температурой и излучать, позже Хокинг более подробно описал это излучение, которое назвали в его честь, но это уже совсем другая история.
Закончу пост цитатой Эйнштейна:
«Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область ее применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута»
Эйнштейн А. Собр. науч. трудов М.: Наука, 1967. Т. 4. с. 270
Вечный двигатель
Решил погуглить, сколько в среднем потребляет кондиционер...
Мне кажется автор не учëл энергию, которую тратит кондиционер, на вращение в гробу отцов термодинамики.
P.S. На самом деле, становится очень грустно, от количества шлака, которое выдается в выдаче.
P.P.S. ссылку не прикладываю, чтобы не накручивать просмотров этому, несомненно полезному ресурсу
UPD дополнение #comment_205981669
Хитрый, расчетливый и нереальный: кто такой демон Максвелла
В конце XIX века британский физик Джеймс Максвелл предложил мысленный эксперимент, который, казалось бы, нарушает законы термодинамики. В итоге центрального персонажа этого эксперимента назвали демоном Максвелла. Попробуем разобраться, чем же примечательна эта вымышленная сущность.
Демон Максвелла — гипотетическая сущность, предложенная Джеймсом Клерком Максвеллом в одном из его мысленных экспериментов, предположительно, в 1871 году.
При чем тут демон и Максвелл? В общем говоря, сущность, предложенная Максвеллом, — эдакий противоречащий бог из машины, можно сказать, обнаруживший способ обойти один из самых фундаментальных и неоспоримых законов Вселенной — второе начало термодинамики. Изначально коллеги ученого не восприняли мысленный эксперимент всерьез и даже были сбиты с толку, ведь эта «сущность» могла означать, что наконец-то можно забыть о трате угля и просто бесконечно получать работу, по сути, из ничего.
Однако в реальности все не совсем так. О втором законе термодинамики и энтропии вы можете прочитать в другом нашем материале. А сейчас мы попробуем разобраться, почему демон Максвелла вызвал недоумение у светочей науки конца XIX века.
Демон Максвелла — лазейка в энтропии
Изначально мысленный эксперимент Максвелла был упомянут в переписке ученого с Питером Тейтом примерно в 1867 году. Позже он был представлен общественности в книге Максвелла о термодинамике под названием «Теория теплоты» (Theory of Heat), опубликованной в 1872 году.
Джеймс Клерк Максвелл / © Gresham College
Несмотря на то что сам Максвелл никогда не использовал слово «демон», описывая эксперимент, его агент открывал дверь (в перегородке в нашем ящике с газом) между камерами, как «ограниченное существо». Впервые эту сущность назвал «демоном» Уильям Томсон, известный как Лорд Кельвин, для описания агента Максвелла в журнале Nature в 1874 году. В качестве обоснования он утверждал, что хотел таким образом обозначить посреднический характер сущности и ни в коем случае не собирался делать упор на негативный оттенок самого слова.
Итак, вернемся к эксперименту. Речь идет прежде всего о закрытой системе. Предполагаемый аппарат состоит из простого кубоида, в котором содержится какой-то произвольный газ. Кубоид разделен на две секции равного размера с одинаковой, равномерной температурой. На стенке, разделяющей секции, сидит демон, тщательно отбирающий случайным образом разбросанные частицы так, что все частицы с высокой кинетической энергией собираются в одной секции, а остальные — с низкой кинетической энергией — остаются в другой.
Можно сказать, что этот демон — метафора приспособления или машины, способной тщательно анализировать скорость или кинетическую энергию каждой частицы в каком-либо контейнере. Основываясь на своем анализе, приспособление может точно определить, какие частицы ему следует, грубо говоря, оставить себе, а от каких — избавиться.
Слева: две секции, заполненные газом. Справа: демон Максвелла, открывающий и закрывающий дверь в перегородке между секциями / © J. Hirshfield
Между тем это противоречит общепринятому мнению, что частицы газа при постоянной температуре движутся с одинаковой скоростью. Тем не менее эта же скорость — их средняя скорость, а значит, есть частицы, движущиеся с более высокой скоростью, и есть частицы, движущиеся с более низкой скоростью, сводя все к среднему значению.
При помощи этого процесса — действий демона Максвелла — все частицы с высокими энергиями впоследствии загоняются в одну секцию. Демон повысил температуру одной части ящика по сравнению с другой. Эту избыточную температуру или давление можно использовать для питания турбины либо поршня. Да, из этого следует, что мы получаем энергию буквально из ничего. Другими словами, демон уменьшил энтропию, не затратив при этом усилий.
Необходимо понять, однако, что коварный демон применил свои уловки и в итоге смог противоречить закону энтропии, но закон сохранения энергии он не нарушил. Он просто перераспределил случайную кинетическую энергию для создания разницы в давлении, достаточной для получения энергии из изначально уравновешенной системы. Хитрость демона обманула саму природу!
Может ли такой аппарат существовать
Как бы то ни было, подобный аппарат в реальности создать невозможно. Природу не так легко обмануть. Конечно, коварный и умный демон смог избежать гнетущих санкций второго начала термодинамики, но ему никуда не деться от всевидящего ока первого начала термодинамики.
Согласно первому началу термодинамики, никакая машина не способна функционировать без источника тепла, а в процессе работы еще и частично его поглощать. Или же производительность процесса никогда не достигнет 100 процентов. Машинам нужен не только стимул в виде тепла, им еще необходимо впитывать его, тем самым повышая собственную температуру.
Преобразование тепловой энергии в механическую энергию в паровых двигателях не абсолютна. Часть тепла поглощается самим двигателем, понижая общую производительность и повышая окружающую его энтропию.
Если же демон — это высокотехнологичная машина, избирательно отслеживающая определенные частицы, возникает вопрос: откуда он берет энергию для выполнения своей работы? Даже если он каким-то образом умудряется это делать, то расширение в отношении тепловой производительности машины все равно отрицает возможность снижения энтропии.
Переход закрытой системы от низкой энтропии к высокой / ©Socratic
Демону или машине пришлось бы получить информацию относительно частиц. Возьмем, к примеру, фотоны. В процессе взаимодействия с ними сложный аппарат вроде демона Максвелла неизбежно будет тратить энергию и сам впитывать часть тепла, повышая общую энтропию и приводя ее к изначальному значению.
Суть аргумента в том, что, по расчетам, любой демон будет неминуемо «генерировать» больше энтропии, разделяя молекулы, чем он когда-либо сможет ее «уничтожить», — это соответствует принципам, на которых он основан. Другими словами, ему потребовалось бы гораздо больше термодинамической работы для определения скорости молекул и их отбора для прохода через дверь между секциями, чем количество энергии, полученной в результате разности температур, возникшей после проделанной работы.
Как бы то ни было, нельзя не отметить, что Максвелл был весьма хитер. Однако, если бы не первое начало термодинамики, ничто бы не спасло второе начало от публичного позора.