История о том, как клиент вымогает у меня деньги за удаление отзыва на Авито
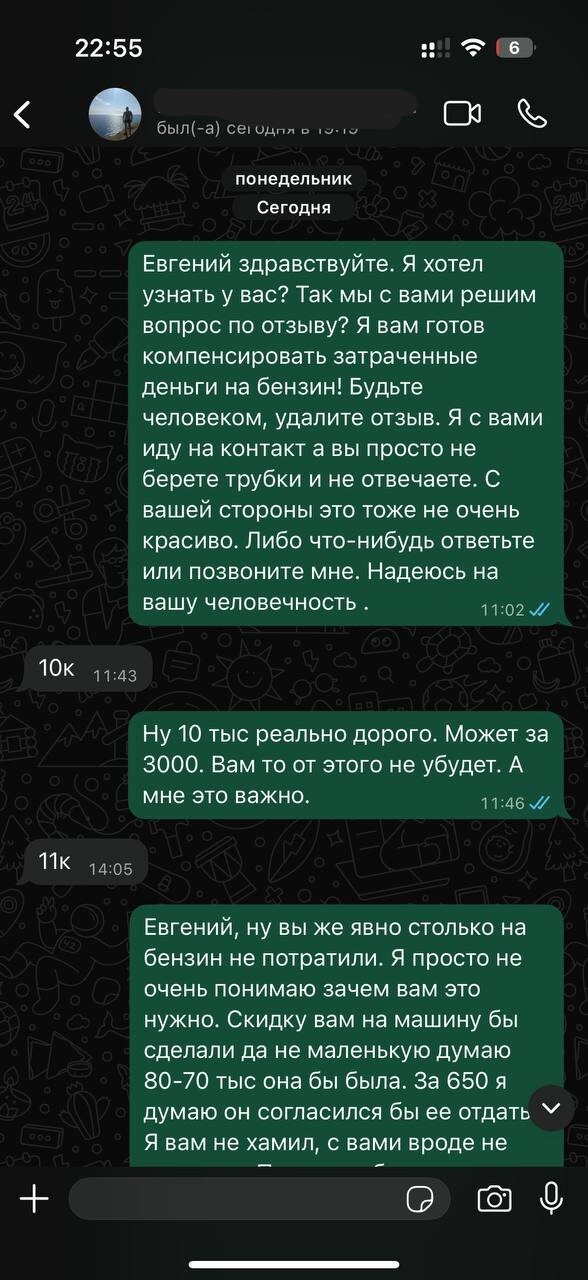
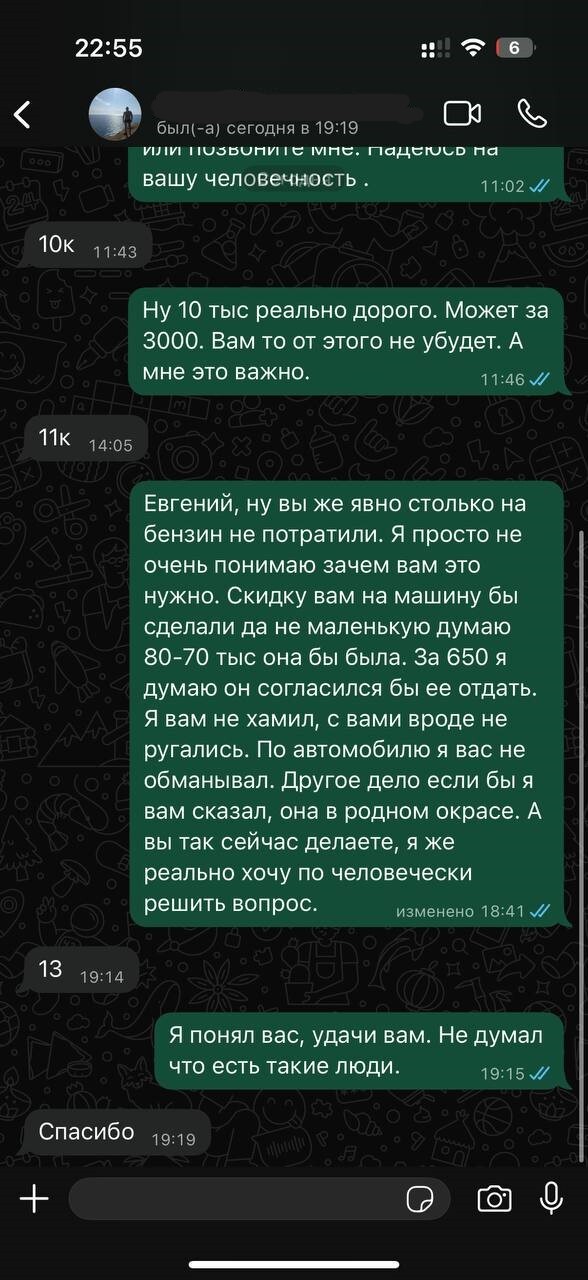
Решил я продать автомобиль на Авито. Звонит человек, спрашивает, можно ли посмотреть его. Я говорю, конечно, приезжайте. Всё рассказываю про данный автомобиль, что он красился. В общем, без обмана. Сейчас все приезжают с приборами, и скрывать что-то смысла нет. Он приезжает, смотрит, ничего плохого не говорит, мы хорошо пообщались. Я готов был сделать хорошую скидку. Он говорит, я подумаю, мы сейчас съездим ещё один вариант посмотрим. Хорошо, на связи. Звонка не было. Ну, думаю, значит, купил другую машину. Захожу в профиль с утра и вижу у себя гневный негативный отзыв. Там написано всё то, о чём я клиенту и рассказывал по телефону. Ничего не скрывая. Сразу же звоню ему, он не берёт трубку. Понимаю, что вряд ли и возьмёт, раз так поступил. Ещё раз, общались хорошо, недовольства со стороны клиента не было. Начинаю писать ему в телеграм и вотсап, скрины прилагаю и видео ссылку на общение с данным клиентом.
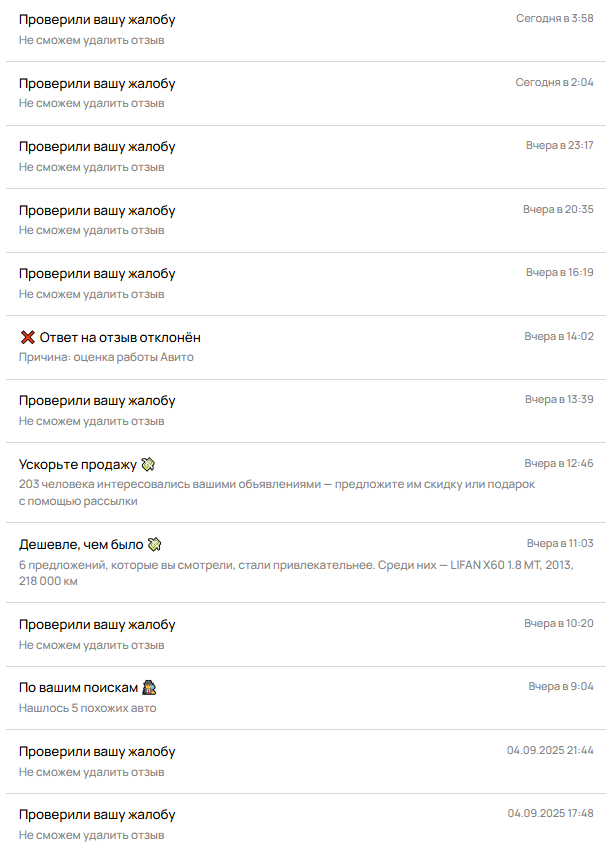
Чтобы решить вопрос, да готов был пойти на уступки, оплатить бензин, извиниться. Хотя не за что извиняться, так как обмана никакого не было. К моему удивлению не было предела, когда он попросил у меня 10 000 тыс. рублей за удаление отзыва. Вот тут я подумал, что это просто разводняк. А потом цена начала расти с каждым новым моим сообщением. И дошла уже до 13 000 тысяч рублей, чтобы данный отзыв был удалён. Смотрите скрины переписки. И тут я понимаю, что у меня вымогают просто тупо деньги. Я начал писать в Авито-поддержку, что меня шантажируют и пытаются просто развести на деньги. На что поддержка отвечает: нам не хватает доказательств. Так я написал в поддержку 9 запросов, а то и больше, и ответ один и тот же, шаблонный. И вы, как площадка, этому способствуете. Поддерживаете мошеннические действия и пишете шаблонные ответы, хотя какие доказательства ещё нужны. Всё и так очевидно, все доказательства я приложил. Номер его телефона на переписке совпадает с его профилем на авито. И вы это тоже знаете.
Элой | Серия игр Horizon Zero Dawn и Horizon: Forbidden West
Опята
Хитрый братец Лис
В меру пузат и не в меру пушист. Совсем крохотуля, до 9см очарования. Связан из пряжи с козьим пухом. Мягкий, милый пушистик. Можно сделать брелок)
Лет 5 назад вычитал в википедии про крупные задачи в математике за которые дают еще и миллион долларов
Лет 5 назад вычитал в википедии про крупные задачи в математике за которые дают еще и миллион долларов.
Одну там Перельман решил еще недавно, помните и отказался от денег.
И там среди них есть одна задача, которая меня заинтересовала - проблема равенства классов сложности P и NP.
Чтобы весь пост не объяснять детально, попробую основное объяснить - суть в том, чтобы доказать что сложные задачи можно решать также просто как и простые задачи, либо доказать, что нельзя.
Это очень грубое пояснение, но суть примерно верна. Основным мерилом простоты задачи считается, то насколько быстро компьютер может ее посчитать. Как на картинке P - операция умножения - это за секунду считается самым дешевым калькулятором. NP - в примере судоку, тут уже может быть нужен более мощные процессор и больше времени.
Я прям очень увлекся одно время этой задачей, и в качестве практического примера сложной задачи для которой можно найти простое решение рассматривал алгоритм шифрования.
Шифрование само по себе быстро происходит, часть ключа получается из перемножения двух 2048-значных чисел. Это простая задача. А вот получиться обратно из результата перемножения два множителя - это намного более сложная задача, поэтому шифрование и относительно безопасно - злоумышленникам нужны большие вычислительные мощности чтобы перебрать варианты множителей.
В общем я к чему. Миллион долларов я не получил, как вы поняли, но в задаче продвинулся немного. У Ферма есть алгоритм как раз для похожей задачи Метод факторизации Ферма - поиск множителей.
И тогда несколько лет назад, я его математическую логику воплотил в код калькулятора и повыполнял на разных числах.
И я пришел к следующему: для некоторых чисел решение находится очень быстро (может вообще за 1 шаг), а для некоторых может вообще не найтись за вечность. Для некоторых других чисел поиск множителей более эффективен другим алгоритмом, например числовым ситом или даже прямым перебором (все зависит от числа).
Таким образом получается, что прям универсального решения нет, но при этом в некоторых случаях можно решать задачу значительно быстрее.
Такая неточность/ненадежность алгоритмов сначала показалась мне тупиком и я дальше не стал развивать исследование.
Однако, за эти годы и особенно в последние годы такие приблеженные вычисления стали все более актуальны и допустимы во многих сферах.
Один из ранних примеров для меня это быстрый обратный квадратный корень Кармака - посчитать симуляцию света в игре на железе тех лет было очень дорого, поэтому он считал приближенно, и это было прорывом и свет все равно прикольно выглядел, даже пусть и неточно считался. В случае компьютерной игры это допустимо.
А теперь когда везде ИИ я прямо прозрел. Вот же она самая проблема P и NP и мои наблюдения о приближенных вычислениях теперь повсюду.
LLM часто ошибается, а генерация изображений выдает 6 пальцев тоже часто. Но скорость вычислений, и возможность иногда получить точный ответ или хорошую картинку на которые бы ушли дни, недели или месяцы - окупает с лихвой эту неточность.
Если бы я знал как эти мысли еще оформить в математический язык, то может быть и получил бы миллион долларов, что думаете?
По идее даже в высокоточных сферах - где цена ошибки дорога - хирургия, космонавтика или какой-нибудь трейдинг - приближенные быстрые вычисления с допустимым каким-то уровнем погрешности будут супер эффективны.
Можно притянуть приближенное решение в качестве аргумента, что P = NP? наверное нет. Но наверное можно вместо равно поставить другой знак P ≈ NP - вот и решение проблемы на миллион долларов.