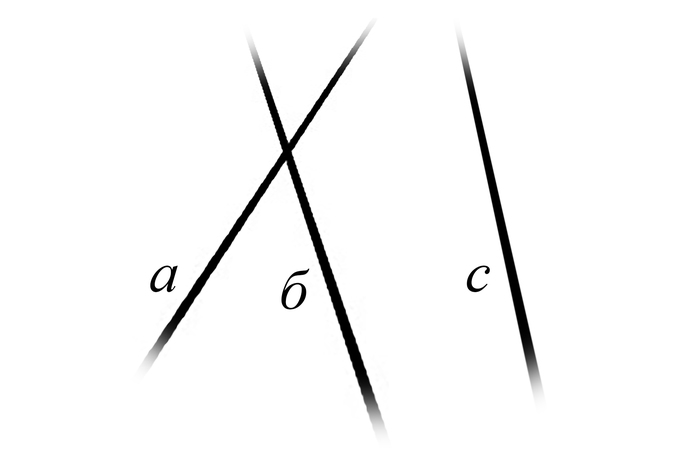Данная статья относится к Категории: Построение научных теорий

«Совершенно ясное и строгое понимание дедуктивных схем пришло лишь в начале XX столетия. В основном это заслуга великого немецкого математика Гильберта. В несколько огрублённой и упрощённой форме дело обстоит примерно так. Мы ограничимся дальше, конкретным случаем геометрии, чтобы не слишком увлекаться абстракциями.

Этап № 1. Перечисление Основных Понятий.

Фундамент - Основные Понятия (либо Основные Элементы). Они - результат длительного экспериментального изучения природы, сложного, путаного, туманного и т. д. и т. д. пути. В итоге, как некое абстрактное отражение реальности, возникают Основные Понятия. О них в аксиоматике не говорится ничего. Они как бы даны свыше. Это естественно. Определять Основные Понятия можно лишь при помощи других новых понятий, те, в свою очередь, при помощи... и так далее до бесконечности. Надо же с чего-то начинать. Как говорят французы: «Чтобы сварить рагу из кролика, необходимо поймать хотя бы кошку».

Итак. Основные Понятия. Математики говорят прелестно: это элементарные объекты, которые не определяются, а лишь называются. Впрочем, маленькое добавление есть.

В современной аксиоматике геометрии Основные Понятия делятся на две группы:

а) Основные Образы;

б) Основные Соотношения.

Вообще говоря, сейчас есть по меньшей мере две существенно различные аксиоматические схемы. Дальше мы будем пользоваться той, в которой Основные Образы таковы:

1) точка;

2) прямая;

3) плоскость.

Теперь посмотрим, что представляют собой Основные Соотношения. Они формулируются так:

1) принадлежать;

2) лежать между;

3) движение.

Основные Понятия установлены. Теперь можно перейти ко второму этапу

Этап № 2. Основные Аксиомы.

Для наших Основных Понятий мы высказываем целый набор утверждений, которые принимаем без каких-либо доказательств. Это аксиомы. Формально говоря, только аксиомы наполняют наши Основные Понятия живым содержанием. Только они дают им жизнь. Без аксиом Основные Понятия вообще лишены какого-либо содержания. Они - пустой звук. Аморфные призраки. Аксиомы определяют правила игры для этих «призраков». Устанавливают чёткий логический порядок. И лишь одно может сказать математик о своих Основных Понятиях - они подчиняются таким-то и таким-то аксиомам. И всё. Всё!

Потому что математик, собственно, не знает, о чём он говорит. Единственное, что он требует: выполнения своих аксиом. Единственное! Когда аксиоматический метод доведён до совершенства, геометрия, говоря формально, превращается в абстрактную логическую игру. «Точка», «прямая», «плоскость», «движение» - под этим может скрываться все что угодно. Любые объекты. Мы построим для них геометрию. И мы будем называть нашу геометрию геометрией Евклида, если будут выполняться аксиомы, установленные для «настоящей» геометрии Евклида. Например: через две различные точки проходит одна, и только одна, прямая. Это аксиома, сформулированная на обычном языке.

Если строго придерживаться терминологии, введенной чуть ранее, надо было бы сказать так: двум различным точкам может принадлежать одна, и только одна, прямая. И далее в том же духе. Как хорошее упражнение рекомендую на основе этой аксиомы доказать теорему: «Две прямые имеют лишь одну общую точку».

Всего в евклидовой геометрии сейчас различают пять групп аксиом. Это:

1) аксиомы соединения;

2) аксиомы порядка;

3) аксиомы движения;

4) аксиома непрерывности;

5) аксиома о параллельных.

Вряд ли стоит сейчас перечислять все эти аксиомы, мы поместим их в приложении, памятуя слова Геродота, что ничто не придаёт книге такой вес и солидность, как приложения. К аксиомам мы ещё не раз вернёмся, а пока укажем...

Этап № 3. Перечисление Основных Определений.

При помощи Основных Понятий мы строим более сложные. Например: угол - это фигура, образованная двумя полупрямыми (лучами), исходящими из одной точки. Если внимательно прочитать эту фразу, станет ясно, что в определении угла использовано одно сложное понятие, а именно: «луч» - полупрямая.

Очевидно, мы должны были раньше дать определение этого понятия при помощи Основных. Это довольно легко можно сделать. Читатели могут проверить, насколько они прониклись духом дедукции, и, вооружившись списком аксиом, попытаться решить эту задачу.

Если бы оказалось, что, используя Основные Понятия, невозможно определить, что такое луч, тогда пришлось бы это понятие отнести к Основным.

В общем все остальные понятия и определения вводятся при помощи Основных, а также (внимание!) тех аксиом, которые установлены нами для Основных Понятий. Нам остался последний...

Этап № 4. формулировка теорем. Доказательство теорем.

Для наших понятий (Основных и неосновных) мы высказываем утверждения-теоремы, которые и доказываем. Это, собственно, и есть предмет геометрии. Я сейчас ещё раз хотел бы повторить, что в такой постановке геометрия превращается в совершенно абстрактную игру наподобие шашек либо, ещё лучше, шахмат.

Там также есть Основные Понятия - фигуры. Есть аксиомы - совокупность правил игры. И наконец, есть теоремы. Собственно, одна теорема: как поставить противнику мат.

Для решения этой «теоремы» игрок в ходе партии доказывает десятки лемм (вспомогательных теорем), выбирая всякий раз лучший, по его мнению, ход в данной позиции. Впрочем, отличие игр от геометрии есть. Оно состоит в том, что очень часто партнёрами принимаются неправильные «доказательства». В шахматах, скажем, не сформулированы (неизвестны) строгие логические критерии оценки каждого хода или позиции. В геометрии они есть. В ней всегда можно установить, что вновь сформулированная теорема противоречит предыдущим теоремам, а значит, противоречит и более ранним, а значит... Разматывая клубок до конца, мы приходим к двум возможностям.

Или мы допустили ошибку в нашем рассуждении, или теорема, которую мы вновь сформулировали, ошибочна.

Первая возможность малоинтересна для науки; она показывает лишь то, что мы плохо владеем математикой.

Зато во второй содержится определённый и часто очень важный результат. Если мы убедились, что наша гипотеза (теорема) неверна, следовательно, верны другие теоремы, именно те, что противоречат нашей. Если таких противоречащих теорем лишь одна, то вашим рассуждением мы её доказали.

Последним абзацем, возможно в излишне туманной и абстрактной форме, мы разобрали схему очень распространенного в геометрии (как и вообще в математике) метода «доказательства от противного». Или по-другому - метода «приведения к абсурду» (reductio ad absurdum)».

Смилга В.П., В погоне за красотой, М., «Молодая гвардия», 1968 г., с. 32-36.

Источник — портал VIKENT.RU

Изображения в статье

Евклид — древнегреческий математик, первый математик Александрийской школы / CC BY-SA 3.0

Image by Alexas_Fotos from Pixabay

Image by Med Ahabchane from Pixabay

Image by Vural Yavaş from Pixabay

15:21, июль, 32 градуса по Цельсию.

Иду, слушаю лекцию про аксиомы Евклида и геометрию Лобачевского через наушники по прилегающей территории с приоритетом движения пешеходов, неразмеченная автомобильная парковка перед магазином Перекресток. И тут некий молодой водитель, сдавая машину задним ходом и разговаривая по сотовому телефону, на достаточно высокой скорости попытался занять парковочное место, через которое пролегал мой путь в данный момент. Подозреваю, преследуя цель припарковать свое транспортное средство поверх меня... Не скрою.. Я был несдержан в словах описательного свойства, детально выражавших мое отношение к намерениям данного водителя и его водительских навыкам.

Навязчиво преследуя, зайдя за мной в торговый зал, в весьма агрессивной форме уже не водитель но молодой примат предложил выйти из магазина, видимо, для восстановления своих субъективных представлений о поруганной чести моими, отнюдь, нелестными высказываниями в свой адрес... Я вышел, далее, руководствуясь его приглашением, нанес удар рукой в область предполагаемого наличия головного мозга у приматов его вида... Несмотря на повторяющиеся приглашения проследовать за ним дальше, ушел в магазин и приобрел томаты, два огурца и немного зелени.

В магазине один из добросовестных граждан предупредил меня о манипуляциях с бейсбольной битой вышеозначенным молодым приматом в багажнике своего авто... По выходу из магазина ко мне подошел еще один примат, по видовым признакам отождествляемый с героем моего рассказа и предложил угостить его сигаретой, в чем ему я не отказал, ввиду природной доброты и чувства взаимопомощи ближнему. Однако, мне показалось подозрительным, что он не уходит по своим делам, а хаотично перемещается, не теряя меня из поля зрения. Я решил не усугублять ситуацию, зашëл в магазин, позвонил брату, он приехал на авто и эвакуировал меня с места событий.

По факту отсутствия обращений от меня в правоохранительные органы поясняю, был голоден и хотел дослушать лекцию про аксиомы Евклида и геометрию Лобачевского.

Алëша. 39 лет. Верю в справедливость.

В среде людей образованных, и даже более того, учёных, отношение к такому предмету познания мира, как философия, мягко сказать, снисходительное. Никто из них, наукой её не считает.

Поэтому, вызывает очень большое удивление тот факт, что такое чисто философское понятие, как "абсолют" (первоначало всего Сущего, вечное и неизменное, единое, бесконечное, и безначальное), было присвоено части классической геометрии.

Случилось это благодаря логическим обоснованиям того факта, что выполняемость первых четырёх постулатов Евклидовой геометрии, ни коим образом, не обеспечивает истинность пятого. Такой вывод был сделан, нашим математиком, Николаем Ивановичем Лобачевским. Именно он предположил, что по крайней мере две пересекающиеся прямые (а и б) могут не иметь ни одной общей точки с третьей (с), если все они лежат на плоскости с уходящими в абсолют границами.

Проще всего понять, данную аксиому, можно сравнив её, с вычислением длинны окружности через произведение диаметра на постоянную пи.

Поскольку, полное значение бесконечной десятичной дроби пи округлено в меньшую сторону, до 3,14, то значение периметра всегда будет меньше истинного. Наращивание, точности вычисления пи, будет постоянно увеличивать длину окружности, но никогда не приведёт к её искомому значению.

В данном примере, бесконечность вычисления, точного значения пи, как раз и будет тем самым абсолютом, не позволяющим пересечься прямым в аксиоме Лобачевского. Разница заключается лишь в том, что пи это конкретное число, а геометрический абсолют является чисто философской величиной. Но тем не менее, это обстоятельство нисколько не ставит под сомнение состоятельность абсолютной геометрии.

Конечно же, философия не имеет такой доказательной базы, как точные науки, а на голой логике быть достаточно убедительным невероятно сложно, но раз уж есть такой прецедент, когда математики не сочли зазорным опереться на онтологический аргумент, то может быть стоит начать рассматривать её более серьезно?

Телескоп Euclid готов к сборке

Руководство ESA утвердило финальный дизайн космической обсерватории Euclid. Об этом говорится в пресс-релизе, опубликованном на сайте космического агентства. Решение означает, что теперь инженеры смогут приступить к интеграции компонентов аппарата. По классификации ESA, миссия Euclid относится к категории M (сокращенно от medium, т.е. «средний»). Ее бюджет составляет 500 миллионов евро без учета стоимости ракеты-носителя. Телескоп будет запущен в июне 2022 года и выведен на гало-орбиту в районе точки Лагранжа L2 системы Земля – Солнца.

http://sci.esa.int/euclid/60994-key-milestone-for-euclid-mis...

Длина аппарата составит 4.5 м, ширина — 3.1 м, общая масса — 2.1 тонны. Для осуществления поставленных задач, Euclid оснастят 1.2-метровым зеркалом. Телескоп сможет выполнять наблюдения в части видимого и ближнем инфракрасном диапазоне.

Цель миссии Euclid заключается в изучении история расширения Вселенной, формирования ее крупномасштабных структур и распределения темной материи и темной энергии. Для этого обсерватория будет осуществлять высокоточные измерения красных смещений далеких галактик, находящихся на дистанции до 10 млрд лет от Млечного пути. Данные о связи красного смещения и расстояния должны помочь астрономам лучше разобраться в том, как Вселенная приобрела свой нынешний вид.