0 просмотренных постов скрыто
Деление на ноль
прошлый мой пост Доказательство умножения на ноль был посвящен умножению на ноль. И меня очень сильно просили рассказать про деление на ноль.
В данном случае задача из теоретической механики и объяснения для гуманитариев не будет.
Вообще объяснения не будет, а только задача. Кому интересно тот поймёт где возникает деление на ноль.
Задача: Один конец каната закреплен к земле, перекинут через два ролика, на другом конце висит груз.
Какой массой должен обладать груз чтобы под канатоходцем канат не провисал вообще и оставался идеально прямым? Масса канатоходца больше нуля.
Канат можно рассматривать как цепочку цилиндрических шарниров или как структуру у которой полностью отсутствует сопротивление на изгиб. Масса каната равна нулю.
Канат, ролики, крепление к земле, обладают абсолютной прочностью. Трение узлов, сопротивление воздуха и прочие факторы равны нулю.
Те кто утверждает, что делить на ноль нельзя - решите эту задачу по другому.
Показать полностью
1
Решения задач по теор.механике из сборника Кепе О.Э. (Глава 20. Уравнение Лагранжа второго рода)
Ушёл из преподавательства, но преподавание не ушло из меня. Работа в вузе уже давно в прошлом, но теоретическая механика пока в сердечке. Надеюсь хватит сил добить некогда поставленную себе цель и доделать уроки по всем темам задачника Кепе.
Тема 20.1. Обобщённые координаты (задачи с 20.1.1 по 20.1.9):
Тема 20.2. Обобщённые силы систем с одной степенью свободы (1 из 2) (задачи с 20.2.1 по 20.2.10):
Тема 20.2. Обобщённые силы систем с одной степенью свободы (2 из 2) (задачи с 20.2.11 по 20.2.20):
Тема 20.3. Обобщённые силы систем с несколькими степенями свободы (задачи с 20.3.1 по 20.3.15):
Тема 20.4. Кинетический потенциал (задачи с 20.4.1 по 20.4.10):
Тема 20.5. Уравнение Лагранжа второго рода для систем с одной степенью свободы (задачи с 20.5.1 по 20.5.16):
Тема 20.6. Уравнения Лагранжа второго рода для систем с несколькими степенями свободы (задачи с 20.6.1 по 20.6.19):
Спасибо за внимание.
Показать полностью
6
Решения задач по теор.механике из сборника Кепе О.Э. (Глава 19. Общее уравнение динамики)
Пока ещё хватает сил продолжать, а значит продолжаем разбираться с теоретической механикой.
Тема 19.1. Определение обобщённых сил инерции в системах с одной и двумя степенями свободы (задачи с 19.1.1 по 19.1.14):
Тема 19.2. Применение общего уравнения динамики для описании движения системы тел (задачи с 19.2.1 по 19.2.15):
Тема 19.3. Применение общего уравнения динамики для определения внешних воздействий и параметров механических систем (1 из 2) (задачи с 19.3.1 по 19.3.13):
Тема 19.3. Применение общего уравнения динамики для определения внешних воздействий и параметров механических систем (2 из 2) (задачи с 19.3.14 по 19.3.25):
Продолжение следует.
Показать полностью
3
Господа Пикабушники
Прошу небольшого содействия.
Решаю нетривиальную задачу при помощи ИИ.
Условия. (промт)
"Представим полый металлический шар из обычной конструкционной стали внутренним объёмом 1 дм^3, шар заполнен водой без пузырьков воздуха.
Заморозим этот шар для превращения воды в лёд. Рассчитай минимальную толщину стенки шара, при которой он не лопнет от расширения льда. Очевидно, что если стенка шара будет 1мм, то его порвёт, а если 1км, то нет. Толщина стенки может быть любая, лишь бы шар выдержал. Сжимаемостью льда можно пренебречь. "
Прошу тех, кто имеет доступ к умным нейросетям помочь мне перепровериться.
Что ответил Qwen2.5-Plus.
Что ответил DeepSeek.
(Сами расчёты не привожу, дабы не засорять пост излишней информации)
Как мы видим результаты отличаются.
А что ответят GPT, Grok и прочие?
Показать полностью
2
Решения задач по теор.механике из сборника Кепе О.Э. (Глава 18. Принцип возможных перемещений)
Тема 18.1. Связи и их уравнения. Число степеней свободы системы (задачи с 18.1.1 по 18.1.14):
Тема 18.2. Возможные перемещения системы (задачи с 18.2.1 по 18.2.10):
Тема 18.3. Принцип возможных перемещений (1 из 2) (задачи с 18.3.1 по 18.3.13):
Тема 18.3. Принцип возможных перемещений (2 из 2) (задачи с 18.3.14 по 18.3.25):
Спасибо за внимание.
Показать полностью
3
Решения задач по теор.механике из сборника Кепе О.Э. (Глава 17. Принцип Даламбера)
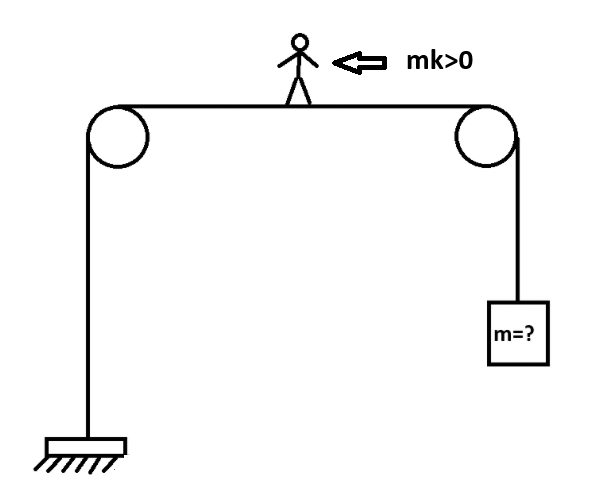
Разбор получился с большим перерывом в связи с рядом обстоятельств, но в итоге ещё одна глава готова.
Тема 17.1. Метод кинетостатики для материальной точки (1 из 2) (задачи с 17.1.1 по 17.1.13):
Тема 17.1. Метод кинетостатики для материальной точки (2 из 2) (задачи с 17.1.14 по 17.1.25):
Тема 17.2. Главный вектор и главный момент сил инерции (1 из 2) (задачи с 17.2.1 по 17.2.11):
Тема 17.2. Главный вектор и главный момент сил инерции (2 из 2) (задачи с 17.2.12 по 17.2.21):
Тема 17.3. Метод кинетостатики для твёрдого тела и механической системы (1 из 4) (задачи с 17.3.1 по 17.3.12):
Тема 17.3. Метод кинетостатики для твёрдого тела и механической системы (2 из 4) (задачи с 17.3.13 по 17.3.24):
Тема 17.3. Метод кинетостатики для твёрдого тела и механической системы (3 из 4) (задачи с 17.3.25 по 17.3.36):
Тема 17.3. Метод кинетостатики для твёрдого тела и механической системы (4 из 4) (задачи с 17.3.37 по 17.3.47):
Тема 17.4. Определение динамических реакций подшипников (1 из 2) (задачи с 17.4.1 по 17.4.11):
Тема 17.4. Определение динамических реакций подшипников (2 из 2) (задачи с 17.4.12 по 17.4.21):
Когда ушёл из преподавателей, но преподаватель не ушёл из тебя.
Показать полностью
9
Ответ Pokryshkin в «Зачем мы учили алгебру»14
Может, лучше изучать теоретическую механику начального уровня в школах? Нет, ну а что? Тоже вроде как узкоспециализированный предмет, однако не так оторванный от реальной жизни, как эти ваши алгебры. Математические формулы есть, да, но они относительно простые, там нет абстрактных вычислений ради самих вычислений.
А-ха-ха, блин, хорошая шутка.
Открываем третью страницу (не считая предисловия) в самом известном учебнике по теормеху:
Ну ладно, не будем пугать детишек Ландафшицем, возьмём простенький учебник теормеха. Там на первых трех страницах ничего страшного нет, давайте отмотаем еще несколько:
Или третий учебник:
Несложно. Не Ландафшиц. В принципе, можно дать уже второкурснику или даже в весеннем семестре первого курса. Но кто не разобрался в школьной алгебре, тем в теормехе делать нечего, даже вводные параграфы не поймут.
Или еще учебник Вильке. Вы не смотрите, что параграф номер 2.1: это первый параграф книги после предисловия и исторической справки.
Или вот еще:
Сдаётся мне, вы путаете теоретическую механику с каким-то другим предметом.
Показать полностью
5