Может кто-то может подсказать по какой формуле решается такая задача : есть 4 цветка: 2 розы, астра и тюльпан и два цвета. Сколько вариантов расцветок может быть. Нагуглила формулы, но мои гуманитарные мозги не могут их применить к конкретной ситуации.
Ну а если бы кто-то запилил пост для чайников, было бы чудесно.
Данная статья относится к Категории: Построение научных теорий
Г.В. Лейбниц опубликовал первые главы своей «Диссертация о комбинаторном искусстве отдельным изданием» и под названием: «Арифметическое исследование комплексий».
«Поскольку универсум, по Лейбницу, представляет собой гармоническую совокупность вещей, находящихся между собой в определённых математически исчисляемых отношениях, то комбинаторика является для него фундаментальным методом, позволяющим с формалистической точностью производить две основные операции познания - анализ и синтез. […]
… Следовательно, согласно Лейбницу, задача комбинаторного искусства заключается в том, чтобы:
а) разложить все сложные вещи и понятия на простые элементы, которые сами уже не поддаются дальнейшему разложению и могут быть поняты только через аналогию; найденные таким образом первопринципы и будут представлять собой «алфавит человеческих мыслей», редукция к которому позволяет достигнуть точного знания о вещах;
б) выявить все возможные новые комбинации этих первопринципов, в результате чего будут получены новые, в том числе и производные истины; это и есть задача изобретательной логики.
По мысли Лейбница, комбинаторный метод приращения знания равно применим в самых различных областях, а потому оказывается пригоден для создания той самой «всеобщей науки», над проектом которой работали современники Лейбница - Эрхард Вейгель и Атанасиус Кирхер (1602-1680).
В главе «Применение Задач I и II», где сосредоточено основное философское содержание «Диссертации», Лейбниц обстоятельно аргументирует следующий тезис: подобно тому, как в геометрии Евклида действует закон первоначальных аксиом, так и во всех прочих науках должны быть установлены первопринципы, из которых путем комбинирования по определённым правилам выводились бы все прочие содержания.
«Юриспруденция же, - поясняет он этот тезис на примере, - во всём похожа на геометрию, разве что в одном случае имеются элементы, в другом казусы. Простыми элементами в геометрии являются фигуры: треугольники, круги и пр. В Юриспруденции же - действия, обязательства, право продажи и пр. Казусами являются их комплексий, и здесь и там они изменчивы до бесконечности». Аналогичным образом комбинаторный метод применим, по мысли Лейбница, в медицине, натурфилософии, музыке, военном деле и стихосложении. Лейбниц считал также возможным создание на комбинаторной основе универсального языка.
Однако наиболее существенным нововведением Лейбница в этой области является применение комбинаторики к интерпретации силлогистики. Именно здесь берёт начало знаменитый принцип Лейбница «praedicatum subjecto inest». В соответствии с этой концепцией, сложное понятие всегда содержит в себе простые, из которых оно составлено, точно так же как в суждении субъект содержит в себе все предикаты, которые могут быть ему приписаны посредством высказываний. Истинность предложения состоит в том, что понятие, образующее предикат, содержится в понятии, образующем субъект. Это относится ко всем без исключения предложениям, как необходимым, так и контингентным, как всеобщим, так и относящимся к единичностям. Соответственно, комбинаторика предоставляет логический метод, в котором сложение и разложение понятий могут быть произведены в условиях механического контроля, так что эта методика открывает путь к формализации аналитической теории понятий и суждений, а тем самым и к задуманной «ars demonstrandi» и «ars inveniendi». […]
В «Диссертации о комбинаторном искусстве» Лейбниц не только перечислил все луллиевы термины, но и произвёл те комбинаторные исчисления, которые Луллий представлял сугубо теоретически. Это обстоятельство убедительно свидетельствует о том, сколь основательно Лейбниц был знаком с луллиевым методом. Лейбниц подсчитал общее число комбинаций, которые можно получить из девяти понятий каждого класса и которое составляет: 511 = 29 - 1, а также общее число комбинаций, получающихся при соединении любого термина одного класса с любым термином другого класса: 5116= 17.804.320.388.674.561. Однако, подхватывая общую идею комбинаторики, как её сформулировал Луллий, Лейбниц видит свою задачу не столько в усовершенствовании математического аппарата комбинаторики, сколько в осуществлении философской ревизии изобретённой Луллием комбинаторной машины.
В «великом искусстве» Луллия Лейбниц не мог принять два изначальных допущения: во-первых, то, какие именно понятия были выбраны Луллием в качестве основополагающих и элементарных, а во-вторых, их количество, ради симметрии искусственно ограниченное девятью элементами в каждом классе. Кроме того, Лейбниц оспаривает необходимость обособления некоторых групп, например, класса вопросов, которые дублируют атрибуты, а также класса добродетелей и грехов, которые очевидно не являются элементарными и всеобщими понятиями. Эти замечания позволяют двадцатилетнему Лейбницу сделать вывод, что метод Луллия «скорее подходит для того, чтобы говорить о вещах, чем для достижения полноценного знания о них».
Свою задачу Лейбниц видел в том, чтобы реформировать луллиевскую комбинаторику, не только снабдив её более совершенным математическим аппаратом, но и придав ей характер строгого философского знания. Сущность лейбницевского метода заключалась в следующем.
Все понятия делятся на классы. В первый класс входят простые понятия, схватываемые либо через определения, либо через аналогию. Согласно Лейбницу, этот класс составляют «не только вещи, но также состояния (modi) и отношения (respectus)». Эти элементарные понятия должны быть помечены определёнными знаками, лучше всего - пронумерованы. Во второй класс входят понятия, полученные в результате комбинаций двух понятий первого класса. Третий класс составляют понятия, полученные в результате комбинаций трех понятий (Лейбниц называет это контернацией) первого класса, и так далее. Таким образом, каждое сложное понятие может быть записано в виде формулы, представляющей собой его определение. В целях упрощения этой записи Лейбниц прибегает к форме дроби, где числитель соответствует определённому порядковому номеру простого термина, а знаменатель представляет экспоненту, обозначающую общее число простых терминов, входящих в комплексию, то есть указывает на порядок класса. (Понятия комплексии и экспоненты, а также другая терминология комбинаторного метода вводятся Лейбницем в главе «Определения», вошедшей в состав «Арифметического диспута»). Например, запись 1/2 будет обозначать первый термин второго класса, 2/3 - второй термин третьего класса, и так далее.
При помощи этого метода Лейбниц предполагает возможным определение производных понятий через простые, входящие в него в качестве множителей, точно так же как, например, число 210 может быть представлено в виде произведения чисел натурального ряда 2, 3, 5, 7.
Соответственно, этот метод позволяет найти (логически) все предикаты к заданному субъекту. Действительно, множители записанного в виде дроби понятия как раз и будут представлять собой его предикаты, так как они выражают, все вместе и каждый в отдельности, характеры или качества, входящие в определение понятия. Каждый из этих множителей может быть приписан заданному субъекту, точно так же и каждый, полученный за счёт дальнейших комбинаций простых множителей. Лейбниц также приводит формулу, согласно которой может быть найдено общее число всех возможных предикатов.
Если субъект S составлен из простых понятий, число которых равно к, то ему можно приписывать как предикат любую возможную комбинацию из к элементов, то есть 2к - 1 предикатов. Обратная задача - найти все возможные субъекты для данного предиката - сводится к следующему: необходимо найти все комбинации, содержащиеся в некой данной комбинации. Эти инвариантные элементы в искомых комбинациях и есть то, что Лейбниц называет caput. Если к - число простых понятий, из которых составлен данный предикат, n - число всех имеющихся простых понятий, то число искомых комбинаций, могущих выступать в качестве субъектов, равно 2n-к - 1.
Впоследствии Лейбниц признавал, что математическая ценность его юношеского трактата о комбинаторике невелика. Однако следует учитывать, что это сочинение занимает важнейшее место в формировании философских воззрений Лейбница, которые он развивал и разрабатывал в течение всей жизни. Здесь можно найти первые подступы к учению об универсальной характеристике, или логической алгебре, которая предполагает замещение понятий комбинациями знаков, и, соответственно, предложений - отношениями между этими знаками. Сведя суждение к исчислению, Лейбниц полагает найденный метод универсальным и безошибочным, позволяющим одновременно и устанавливать истинность уже известных высказываний, и производить новые.
«В философии, - писал Лейбниц в третьем письме герцогу Брауншвейгскому и Люнебургскому Иоганну Фридриху, - я нашёл средство осуществить во всех науках то, что Картезий и прочие сделали посредством алгебры и анализа в арифметике и геометрии, с помощью искусства комбинаторики, каковое Луллий и Кирхер хотя и усердно взлелеяли, но далеко не уяснили самую его глубинную сущность. С его помощью пролагается путь к тому, чтобы все сложные понятия всего мира свести к нескольким простым как их алфавиту, а затем из этого комбинаторного алфавита со временем вновь найти все вещи, вкупе с их теоремами, и все, что в отношении их еще может быть изобретено, при помощи правильного метода. Каковое изобретение, поскольку оно, если того Бог пожелает, будет осуществлено, почитается мною за наиважнейшее как мать всех изобретений, хотя в настоящее время оно таким и не кажется. Я уже нашёл с его помощью всё, что должно быть исчислено, и надеюсь дать ход также и многому другому»
Осминская Н. А., Математика и метафизика в «Диссертации о комбинаторном искусстве» Г.В. Лейбница, журнал «Вопросы философии», 2011 г., N 2, с.153-154 и 156-157.
Изображения в статье
Лейбниц, дискурс о метафизике / Public Domain
Image by klimkin from Pixabay
Image by Bruno /Germany from Pixabay
Image by StartupStockPhotos from Pixabay
Image from Pixabay
Задача на комбинаторику. У меня сохранился ее текст вот в таком варианте. Нет 6 пункта, решить невозможно :(
Вдруг кто-то ее узнает... надежды мало, но друг...
Исходные данные (сразу оговорюсь: "соседствуют" - значит, растут в одном саду).
Плодовые деревья: Яблоня, Груша, Слива, Вишня, Черёмуха.
Ягодные кустарники: Крыжовник, Смородина, Облепиха, Малина, Ирга.
Овощи: Огурцы, Помидоры, Редис, Перцы, Свёкла.
Зелень: Укроп, Петрушка, Базилик, Лук, Руккола.
Цветы:
Тюльпаны, Ирисы, Розы, Пионы, Маки.
1. Луковая грядка не соседствует ни с яблонями, ни со смородиной. В грушевом саду нет ни ирги, ни перцев. Ирисы и базилик растут у разных владельцев.
2. Черёмухи нет в саду с огурцами (в котором нет и крыжовника с малиной). Хозяин свекольной грядки (не соседствующей с кустами ирги) даже не слыхал о новомодной рукколе. Вишнёвый сад (в котором нет крыжовника) - не то место, где растёт укроп.
3. Любитель груш не выращивает ни помидоры, ни облепиху. Ни сад с иргой (в котором нет лука), ни
яблоневый сад не украшают пионы. Ни поклонник укропа, ни любитель перцев не выбрали для себя крыжовник.
4. Ни в саду со сливами, ни у любителя свёклы нет луковой грядки. На участке с облепихой (где не растёт вишня) нет рукколы. В грушевом саду не найти ни базилика, ни пионов.
5. Тот, кто всегда мечтал о черёмухе под окном, не стал сажать перцы. А тот, кто рассчитывает поесть борща из собственноручно выращенной свёклы (и при этом равнодушен к яблокам), не сеял петрушку. Укропа нет ни у хозяина малины, ни у любителя ирисов.
7. Смородина - не соседка укропу. Рядом с огурцами не видно ни роз, ни маков. Не растут перцы в малине.
Извините за длиннопост, его можно не читать:) У меня один вопрос: какова вероятность, что 4-х или 5-значное число заканчивается на 99? Я не математик, тупо предполагаю, что 1/100. Один процент. Однако вот некий аналитик считает, что 0.01 % . Биномиальное исчисление, так его. Или имеется в виду, что 4 раза из 25?
Один из основателей исследовательского агентства Data Insight Борис Овчинников заявил, что статистику по коронавирусу в России могут фальсифицировать на федеральном уровне.
К такому выводу аналитик пришел, проанализировав официальные данные о приросте числа заболевших COVID-19 в стране в период с 30 апреля по 24 мая. За 25 дней число выявленных случаев четыре раза заканчивалось на 99: 30 апреля федеральный оперативный штаб сообщил, что коронавирус обнаружили у 7099 человек, 8 мая — у 10699 человек, 12 мая — у 10899 человек, 24 мая — у 8599 человек.
Вероятность того, что за 25 дней число новых выявленных случаев будет заканчиваться на 99, составляет 0,011%, «или один случай на 9350 попыток», написал Овчинников в своем фейсбуке. Он просчитал эту вероятность через биномиальное распределение. Овчинников допустил, что это может быть случайность или требование «сверху».
Аналитик отметил, что «достоверность и адекватность» статистики по коронавирусу в России стала быстро сокращаться, начиная с 20 апреля. «Тогда впервые за долгое время (с 4 апреля) количество новых случаев было меньше, чем в предыдущие два дня, и фактически именно с 20 апреля началась первая „полка“, когда до конца месяца, до 29 апреля включительно, по официальным цифрам шел линейный, а не экспоненциальный рост», — пишет он.
Овчинников также сообщил, что первоначально подозревал фальсификацию статистики по коронавирусу только в регионах. «И даже когда 17 мая сразу восемь регионов выдали похожие цифры 97 или 98, я это списывал на случайное совпадение мышления при рисовании цифр, а не на централизацию фальсификаций», — написал он.
«Официальные цифры по количеству заболевших можно выбросить в мусорное ведро — нет никаких оснований считать, что они адекватно показывают динамику эпидемии. Может быть, показывают, может быть, нет — неизвестно. Качество рисованных цифр невозможно и абсурдно оценивать», — заявил Овчинников.
В интервью телеканалу «Дождь» Борис Овчинников сказал, что у него есть «некоторая осторожность и страх» из-за того, что его могут привлечь к ответственности за эту публикацию, но, по его словам, представители власти понимают, что «официальная статистика сильно не дотягивает до адекватного отражения реальности».
В мае газеты The New York Times и Financial Times сообщили, что официальные данные о количестве умерших от коронавирусной инфекции в России не соответствуют реальным. В официальную статистику не попадают 70% смертей, поскольку причиной смерти называют не COVID-19, а основную болезнь человека и осложнения от коронавируса
Решение.
1. Существует очень красивый способ сделать такой куб — так, собственно, и поступили в головоломке «Уникуб». Красим куб в красный цвет. Один из срезов по оси X делаем жёлтым, второй синим. Аналогично Y и Z.
Чтобы перекрасить две противоположные грани уникуба в жёлтый, делим его по жёлтому срезу, и переставляем два кирпича 3×3×1 и 3×1×2 местами. Проводим то же действие по осям Y и Z, и получаем жёлтый куб.
3. Этот способ масштабируется на любое n, так что ответ на третий вопрос тоже утвердительный.
2. n³ кубиков будут иметь 6n³ граней, построенный из них куб n×n×n — 6n². Нет «лишних» граней, каждая будет задействована в какой-то раскраске — потому все внутренние грани будут постороннего цвета. Соответственно, каждый кубик будет иметь не более трёх граней одного цвета.
В частном случае 3×3×3 будем обозначать как «312» кубик с тремя красными гранями, одной жёлтой и двумя синими. В красном кубе центральным будет кубик 033, в жёлтом — 303, в синем — 330. Таких кубиков по одной штуке. Подумаем, как можно красить угловые, рёберные и граневые кубики красного куба.
Центральный:
033 — 1 шт.
Угловые:
303 — 1 шт.
330 — 1 шт.
321 — x шт.
312 — y шт.
Граневые:
123 — z шт.
132 — t шт.
Рёберные:
213 — u шт.
231 — v шт.
222 — w шт.
Подбив баланс (угловых кубиков восемь, рёберных двенадцать, граневых шесть), получаем систему уравнений.
2 + x + y = 8 (8 красных угловых)
2 + t + v = 8 (8 жёлтых угловых)
2 + z + u = 8 (8 синих угловых)
z + t = 6 (6 красных граневых)
y + u = 6 (6 жёлтых граневых)
x + v = 6 (6 синих граневых)
u + v + w = 12 (6 красных рёберных)
Жёлтые и синие рёберные считать бессмысленно: и без того понятно, что переменная x свободная и варьируется от 0 до 6, u = t = x, y = z = v = 6−x, w=6.
Всё, семь способов? Нет: оказывается, кубик 222 хиральный (то есть невозможно совместить поворотом со своим зеркальным отражением).
Их шесть штук, и среди них может быть от 0 до 6 «левых», остальные правые. Семь вариантов. Думаю, не нужно показывать, что у остальных кубиков, у которых хотя бы три грани одного цвета, хиральности нет.
Итого 7·7 = 49 способов.
Заключение
Слово «хиральный» происходит от греческого «хейр» — «рука». Хиральность близка к понятию «асимметричный относительно плоскости», но существует сложная молекула, которая асимметрична, но не хиральна. Её модель можно сделать из проволоки.
Асимметрия нашего мира обнаруживается уже во взаимодействии элементарных частиц. Отсюда растут ноги у правила левой руки и правила буравчика.
Молекулы сложных соединений бывают хиральные. Даже сахар относится к таковым. При этом биологические системы любят (производят, усваивают и т.д.) одну сторону и не любят другую. Например, сахар бывает только «правый», а ибупрофен действует только «левый». При этом многие из асимметричных молекул поворачивают плоскость поляризации света, тем сильнее, чем их больше в растворе — на этом основан несложный способ определения концентрации сахара.
Ножницы делают под правую руку, и если их возьмёт левша (ну или неполный левша, как я), лезвие будет закрывать линию реза. Можно также говорить про левый и правый винт, левый и правый руль автомобиля.
В спорте — бейсбольные стадионы ориентируют по сторонам света так, чтобы солнце не мешало праворуким отбивающим. Боксёров-левшей в высших лигах много, около 25% — из-за более симметричного развития (часто левшей частично переучивают работать правой рукой) и неудобства для правшей. Наиболее известная из фигуристов-левшей — Каролина Костнер.
В компьютерной графике для простоты любят отзеркаливать спрайты, но это иногда приводит к казусу. В какой руке бедуин держит саблю?
В биологических системах хиральность может встречаться в интересном виде. «Левые» и «правые» наземные улитки не спариваются друг с другом, при этом поедающие улиток змеи приспособились именно к правым — потому «белая ворона» левая, хоть и реже правой, чувствует себя неплохо. Бивень кита нарвала (видоизменённый левый зуб) закручен левым винтом. Иногда бывает, что два зуба прорастают в бивни, и оба закручиваются влево.
1. Есть 27 кубиков. Попробуйте выкрасить их грани в три цвета, чтобы из кубиков можно было собрать полностью красный, полностью жёлтый и полностью синий куб 3×3×3. Есть очень красивый способ это сделать.
2. Такая раскраска не единственна. Какие есть способы варьировать её? Сколько существует раскрасок?
3. Можно ли раскрасить 1 млн кубиков в 100 цветов так, чтобы из них можно было собрать куб 100×100×100 любого цвета?
Задача всё-таки довольно известная, кто-то, как я, видел и уникуб живьём, потому «Моё» не пишу.
Немного про RakeSearch - заполнения и интересная частично ортогональная пара!
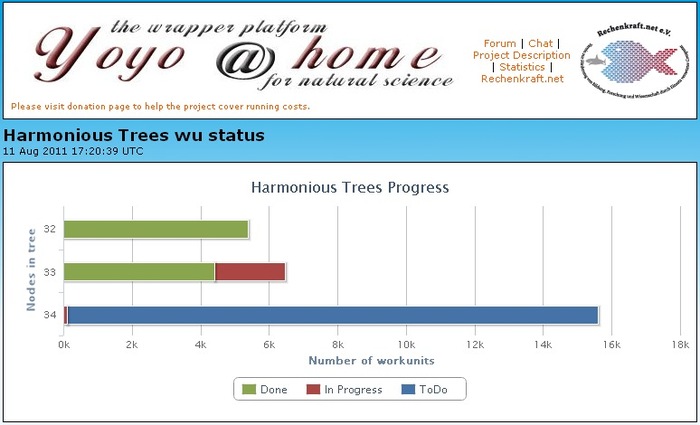
Ранее [ https://vk.com/wall-34590225_292 ] мы рассказывали о новом поиске R10 в рамках проекта RakeSearch, последовавшего за поиском "перестановочных" диагональных латинских квадратов 9 ранга (он же - поиск R9). Сейчас появился повод рассказать о некоторых его деталях!
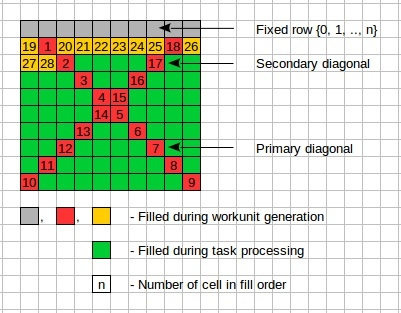
На первом из прицепленных изображений - матрица квадрата 10 ранга, клетки которой раскрашены в несколько цветов:
- серым цветом отмечена верхняя строка с зафиксированными значениями клеток - {0, 1, 2, ..., 9} (выходить за рамки квадратов с такой строкой (они же - нормализованные квадраты) - нет смысла, т.к. ненормализованных квадрат может быть сведён к нормализованному);
- красным цветом обозначены клетки главной и побочной диагоналей, не относящиеся к первой строке;
- оранжевым цветом обозначены клетки первой и второй строки которые вместе с диагоналями и первой (фиксированной) строкой заполняются ещё на этапе генерации, workunit-а;
- зелёным цветом обозначаются клетки, заполняемые во время обработки задания на компьютере участника - вычислительный модуль, заполняя матрицу до конца, формирует всё новые и новые диагональные латинские квадраты и переставляя в них строки, пробует получить ортогональную пару из исходного (только что сформированного) ДЛК перестановкой его строк.
Как вы также можете видеть, все красные и оранжевые клетки пронумерованы в определённом порядке. Это порядок, по которому они заполняются, при формировании комбинации для очередного workunit-а. При этом, клетки самой верхней, фиксированной строки - не пронумерованы потому, что они не меняются и какая бы не получилась комбинация в других клетках - они в ней всегда присутствуют в одном и том же виде.
Интереса ради, мы можем посчитать - сколько же возможно комбинаций, которыми можно заполнить самую первую пронумерованную клетку, или первые две, или три... и так далее. Если получившиеся числа выписать в табличку вида {Число клеток, Число заполнений} то мы получим ряд, возрастающий почти всё время (но не всё время) и с темпом, меняющимся от клетки к клетке. Для первых 28 клеток, пронумерованных на изображении он получается таким:
1 - 8
2 - 57
3 - 356
4 - 1909
5 - 8544
6 - 30637
7 - 82508
8 - 148329
9 - 133496
10 - 934472
11 - 5356527
12 - 26980186
13 - 117013695
14 - 424874652
15 - 1210593966
16 - 2603495520
17 - 3755155200
18 - 2723433984
19 - 17021462400
20 - 82230388428
21 - 341712006852
22 - 1187460703344
23 - 3329849282564
24 - 7024312609228
25 - 9908083279232
26 - 7996577754080
27 - 43965973715660
28 - 212963246290200
Первые ~18 строк этой таблицы (или членов ряда - кому как больше нравится) вычисляются очень быстро - на отдельно взятое число уходят доли секунды, секунды или минуты в один поток, на уже давно выпущенном процессоре Intel Core i5-3570K. Чтобы пойти дальше, надо произвести намного больше вычислений - к примеру, для получения 28 члена ряда потребовалось ~50 суток процессорного времени CPU с архитектурой Haswell.
Но это число - 212963246290200 - интересно и другим. Как говорилось в самом начале, на первом изображении показано заполнение матрицы квадрата при генерации workunit-ов. А это значит, что каждая коминация заполнения этих клеток - это отдельный workunit. А число комбинаций, которыми мы можем заполнить эти клетки, соответственно, это и есть число workunit-ов, которые мы могли бы сгенерировать, если бы решили выполнить поиск по всему пространству ДЛК 10 ранга! Или, 212 триллионов 963 миллиарда 246 миллионов 290 тысяч 200 workunit-ов! Конечно - это слишком много и поиск будет только частичным, по небольшой части от возможно пространства.
Но даже в рамках частичного поиска, можно наткнуться на что-нибудь интересное. И об этом - новость № 2!
В каждом результате, приходящем с компьютера участника проекта, записываются пары со степенью (или "характеристикой") ортогональности более 80. И в каждом результате таких находится как минимум несколько штук. По мере обработки результатов - накапливается статистика о том, сколько пар с той или иной степенью ортогональности было обнаружено. По итогам сентября (то есть, за июль, август и сентябрь вместе взятые) она выглядела следующим образом:
Degree 81: 3887427
Degree 82: 899172
Degree 83: 181014
Degree 84: 33997
Degree 85: 5254
Degree 86: 900
Degree 87: 94
Degree 88: 16
Degree 89: 0
Degree 90: 0
...
Degree 100: 0
Хорошо видно, что переходе к следующей степени ортогональности число найденных пар уменьшается где-то в 4-6 раз. Но при переходе от степени 86 к 87 - разница уже почти в 10 раз (возможно - это временное явление и при дальнейшем накоплении статистики - мы увидим что-то иное), а после степени 88 - уже нет ничего, хотя если бы тенденция соблюдалась, мы должны были бы увидеть от 1 до 3 пар со степенью ортогональности 89!
И вот прошла первая половина октября. Что мы видим в результатах за эти две недели? А вот что:
Degree 81: 1329684
Degree 82: 330656
Degree 83: 74528
Degree 84: 14608
Degree 85: 2624
Degree 86: 400
Degree 87: 47
Degree 88: 6
Degree 89: 0
Degree 90: 1
Degree 91: 0
...
Degree 100: 0
- всё почти тоже самое - даже разрыв между степенями 86 и 87 до карикатурности похож на общую статистику, также нет ни одной пары со степенью 89... но есть 1 пара с 90! К тому же, если мы прибавим число пар с ХО = 88 (ХО - это "характеристика ортогональности", она же - "степень") найденных в первой половине октября к общей статистики, то получим 6 + 16 = 22! А ведь примерно таким (т.е. где-то 25 к 1) и должно быть, судя по статистике, соотношение числа пар на двух ступенях, отстоящих друг от друга на 2 уровня - как в случае с ХО = 88 и ХО = 90! Вот только промежуточное звено с ХО = 89 "куда-то пропало"!
Что это? Какая-то закономерность? Случайность? Что-то ещё? Увидим!
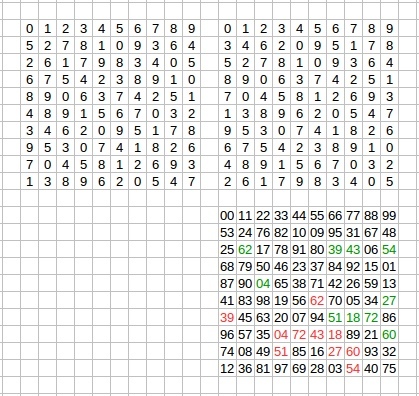
Ну, а саму пару с ХО = 90 - вы можете увидеть на втором из прикреплённых изображений. Нашли её - josef j из команды Russia Team и Thyler Durden@P3D из команды Planet 3DNow! однако вычисления каждого участника приближали эту находку. А может быть, (кто знает?) - и чего-то ещё!
Спасибо за участие и поддержку!
Сентябрь — это не только начало учебного года, но и время активной подготовки к горячему сезону распродаж. Самое время подключить подписку Пикабу+:
рассказывайте о своих товарах и услугах
добавляйте ссылки
создавайте витрину товаров прямо в профиле
подключайте дополнительное продвижение постов
Пора готовить сани!
Проект Yoyo@home
Прежде всего, yoyo@home - это не самостоятельный проект, а платформа на основе технологии BOINC для разных проектов РВ. Очень похожая на нашу Gerasim@Home. На данный момент на платформе yoyo@home работают 4 проекта (все - математические) и уже завершены 7 проектов (1 по физике - Muon и 6 математических).
https://www.rechenkraft.net/yoyo/
https://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9...
OGR. Проект занимается поиском оптимальных линеек Голомба (Optimal Golomb Ruler) порядка 28. Это самый старый проект, реализованный на платформе yoyo@home. На текущий момент OGR-28 выполнен примерно на 70%. Проект является одним из интересных примеров коллаборации между боинковским и не-боинковским проектами РВ: фактически в OGR-28 на платформе yoyo@home используется клиент (вычислительный модуль, экзешник) из не-боинковского проекта distributed.net к которому написан враппер (программа-обертка), позволяющий боинку работать с "чужим" вычислительным модулем. Далее сервера yoyo@home каким-то образом должны обмениваться данными с серверами distributed.net для координации работы по проекту. Примечательно, что клиент distributed.net является самым кроссплатформенным (из всех известных мне): есть версии даже для MS-DOS и Windows 3.1 (но да, под OGR-28 работать будут не все.). Поэтому, кому-то удобнее будет работать непосредственно с нативным клиентом, а кто-то предпочтет Боинк и yoyo@home. Боинк все-таки не под все операционки существует, зато с ним веселее: и соревнования тебе, и сайты статистики, ну и побрякушками (бейджиками) можно обвешаться, хехе. Про антивирусы тоже все верно: зачастую требуется внести экзешники в список исключений.
https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%BA%D1%82%D0%BE...
ECM. Это проект факторизации (разложения на простые множители) целых чисел методом эллиптических кривых (Elliptic Curve factorization Method - ECM). Тоже один из проектов-долгожителей. Факторизации подвергаются числа нескольких видов. Среди них есть и довольно забавные: например, репьюниты, числа, состоящие только из единиц.
https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%BF%D1%8C%D1%8E...
Siever. Проект запущен в 2017 году. Еще один пример коллаборации, но несколько другого вида. "Заказчиком" здесь является проект CRUS, который замахнулся на проверку гипотезы Серпинского/Ризеля для всех чисел вида k · b^n ± 1 с базами b до 1030. Для любой базы b существует аналитическая процедура, позволяющая найти множитель k0 такой, что при всех натуральных n число k0 · b^n + 1 (или k0 · b^n - 1) будет составным. Гипотеза Серпинского/Ризеля утверждает, что k0 - это наименьший множитель из всех возможных. Доказать это можно только перебором: нужно проверить все множители k <k0 и показать, что при каком-то n число k · b^n + 1 (или k · b^n - 1) будет простым.
https://www.mersenneforum.org/forumdisplay.php?f=81
Задача довольно муторная в плане объема работы. Какие-то множители можно сразу выкинуть из простых алгебраических соображений. Какие-то "отвалятся" на численной проверке довольно быстро. Но некоторые, особо упоротые, будут держаться до конца! Например, для базы 2 гипотеза Серпинского/Ризеля проверяется в проекте Праймгрид (подпроекты SoB и TRP). В SoB осталось проверить 5 множителей, в TRP - 49. О вычислительной сложности говорит, например, тот факт, что в подпроекте SoB за 9 лет был исключен всего 1 множитель, а простое число SB10 = 10223·231172165+1 имеет длину более 9 млн. десятичных цифр. В общем, CRUS будут считать ОЧЕНЬ долго. Тем не менее, на данный момент выполнено примерно 38% из задуманного. Как это все считают и для чего здесь yoyo@home? Ну вот у нас есть база: например, Ризель-66, R66 (k · 66^n - 1). Для нее k0=101954772. Большую часть множителей k <k0 мы вычистим математикой и просто сравнением с базой данных простых чисел. Остается 101616 множителей, проверенных до n <11000. Это даже побольше, чем стопиццот, правда? Теперь нам нужно каждый из этих стопиццот прогнать со всеми n>11000 и убедиться, что каждый из них с каким-то n даст простое число. Сделать это можно двумя способами. Либо факторизацией - берем первый попавшийся k (1205) и начинаем раскалывать число 1205 · 66^11001 - 1 на множители. Раскололи - ок, выкидываем 11001, пробуем то же самое с 11002 и так далее. Либо тестом на простоту (primality test) Люка-Лемера-Ризеля (LLR). Он нам факторов не дает, но скажет: простое число 1205 · 66^11001 - 1 или нет. Так вот фишка в том, что пока показатели n маленькие, факторизация работает гораздо быстрее, чем LLR-тест. А потом ситуация меняется на обратную. Поэтому работают с двух сторон: в 2015 году запустили проект SRBase - он занимается LLR-тестами (или Proth-тестами - для Серпинского). А в 2017 на платформе yoyo@home стартовал Siever - он делает просеивание, пытаясь факторизовать числа с небольшими n. Результатом его работы будут т.н. sieve-файлы - в них для каждого множителя k, который не удалось факторизовать, будет указана граница показателя n - та, с которой придется начинать свои LLR-тесты проекту SRBase. Вот такая хитрая схема. А ведь раньше все это делалось энтузиастами проекта CRUS вручную! Впрочем, такая возможность осталась и сейчас.
https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D1%81%D1%82_%D0%9...
http://srbase.my-firewall.org/sr5/
MQueens. Запущен совсем недавно, летом 2019 года. Проект, вычисляющий число расстановок ферзей на шахматной доске M x M, когда они не бьют друг друга. На данный момент проект работает с доской 27 x 27. Для нее результат уже известен. Т.е. сейчас проект занимается проверкой своего алгоритма расчета. После окончания Q27, если все будет хорошо и результат MQueens совпадет с известным, будет запущен Q28 - поиск расстановок ферзей для доски 28 x 28.
