Excel. Долгая дорога оцифровки. Часть 6. Кусочная интерполяция
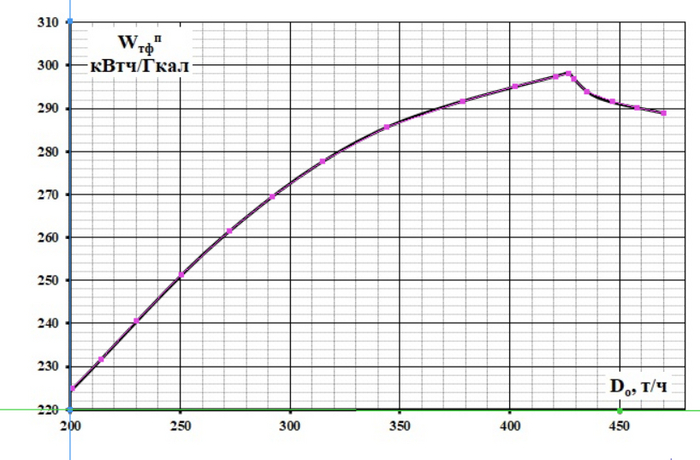
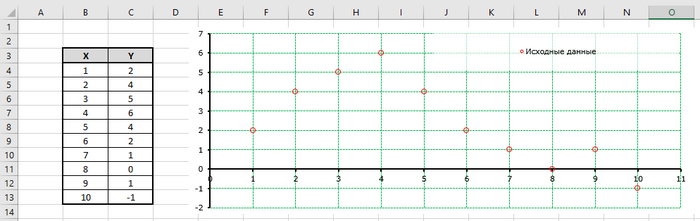
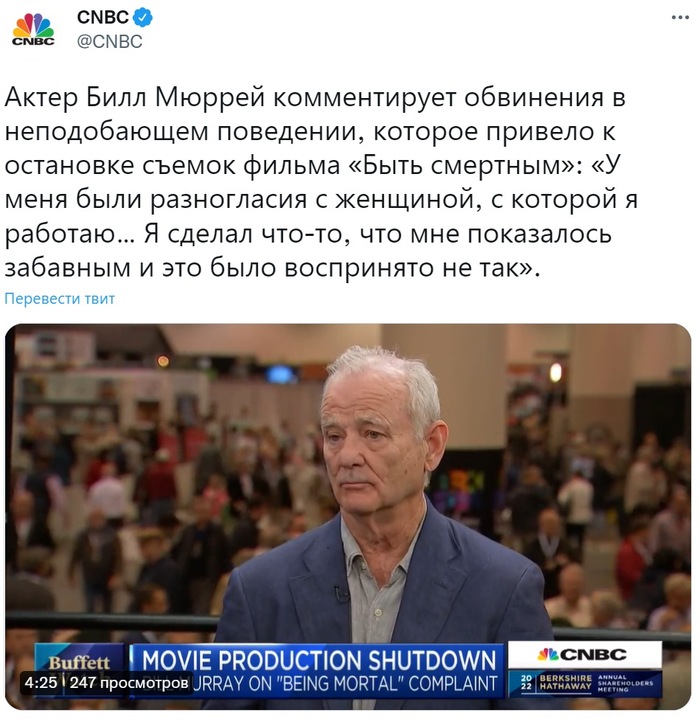
Ну теперь пора перейти именно к интерполяции исходных данных. Итак, я напомню - у нас был лист с распечатанным графиком, мы его отсканировали, получили набор точек ХY и... имеем вот такую (в лучшем случае) картину (см.первый скрин). Т.е. по данному набору точек невозможно сделать корректную апроксимацию полиномом.
Выходом из данной ситуации является разбиение данных на несколько частей, в данном случае 2 с общей точкой Do=428, создание кусучнозаданной функции (ЕСЛИ меньше 428 одна функция, если больше - вторая функция). Но так в данном случае, а если надо сделать два, три...и больше разбиений? Кропотливая работа. Но зачем, если можно заставить Excel в автоматическом режиме выбирать малое количество точек и проводить через них интерполяционную функцию.
Отчасти кусочную интерполяцию показывал в прошлом посте серии ( Excel. Долгая дорога оцифровки. Часть 5. Создание пользовательской функции для двух аргументов. Ручной вариант ) при поиске решения между заданных критериев.
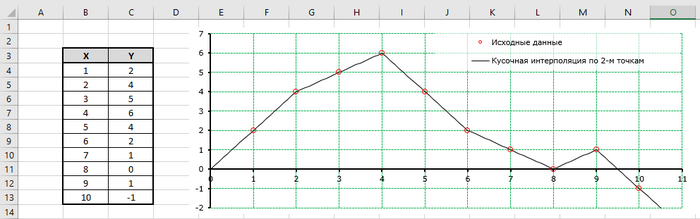
Как простые варианты рассмотрим кусочную интерполяцию по двум и по четырём точкам для заданных ниже данных.
Допустим нужно определить значение Y при X = 2.5.
При кусочной интерполяции по двум точкам используются две ближайшие заданные точки к X = 2.5. , т.е. 2 и 3, через данные точки провидится линия,и по ней находится Y при X = 2.5..
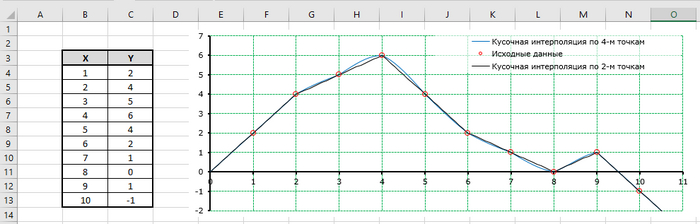
При кусочной интерполяции по четырём точкам используются две ближайшие заданные точки к X = 2.5. справа и две две ближайшие заданные точки к X = 2.5. слева, т.е. 1 и 2 и 3 и 4, через данные точки провидится кривая (полином 3-й степени),и по ней находится Y при X = 2.5.
Это справедливо для данных за 2-й и перед предпоследней известной точкой. Для данных отрезков и для экстраполяции использую линейную интерполяцию (по 2-м точкам).
Как видно использование кусочной интерполяции по 4-м точкам (голубая линия)немного сглаживает итоговую функцию, что позволяет снимать при оцифровке чуть меньше точек :) .
Вообще правило такое, в зависимости от вида графика:
Ну и собственно с помощью чего сие выполняется:
Макрос кусочной интерполяции при использовании данных с листа
======
' Интерполяция по 2-м, 3-м или 4-м ближайшим (до и после) к заданной (Xisk) точке
' В подпрограмму передаются все заданные точки
' Интерполяция происходит косочно, по количеству заданных точек с учётом расположения заданного Х
' Данные из листа Excel.
Public Function kus_interp_Ex(Xt As Range, Yt As Range, Xisk As Single, Optional ByVal toch As Integer = 2) As Variant
Dim i As Long
Dim xd() As Double
Dim yd() As Double
Dim cd() As Double
' toch - указание поиска решения с использованием количества точек (2, 3, 4).
Select Case toch
Case 2 ' Уравнение а·х+b
kus_interp_Ex = linterp(Xt.Rows(Xt.Count - 1), Xt.Rows(Xt.Count), Yt.Rows(Xt.Count - 1), Yt.Rows(Xt.Count), Xisk)
For i = 1 To Xt.Count - 1
If Xisk < Xt.Rows(i + 1) Then
kus_interp_Ex = linterp(Xt.Rows(i), Xt.Rows(i + 1), Yt.Rows(i), Yt.Rows(i + 1), Xisk)
Exit For
End If
Next i
Case 3 ' Уравнение а·х^2+b·x+c Интерполяция по принципу х1 Х х2 х3
kus_interp_Ex = kubterp(Xt.Rows(Xt.Count - 2), Xt.Rows(Xt.Count - 1), Xt.Rows(Xt.Count), _
Yt.Rows(Xt.Count - 2), Yt.Rows(Xt.Count - 1), Yt.Rows(Xt.Count), Xisk)
For i = 1 To Xt.Count - 2
If Xisk < Xt.Rows(i + 1) Then
kus_interp_Ex = kubterp(Xt.Rows(i), Xt.Rows(i + 1), Xt.Rows(i + 2), _
Yt.Rows(i), Yt.Rows(i + 1), Yt.Rows(i + 2), Xisk)
Exit For
End If
Next i
Case 4 ' Уравнение а·х^3+b·x^2+c·x+d Интерполяция по принципу х1 х2 X х3 x4
ReDim xd(1 To 4) As Double
ReDim yd(1 To 4) As Double
If Xisk < Xt.Rows(2) Then ' Экстраполяция ДО и интерполяция ДО второй известной точки - линейна
kus_interp_Ex = linterp(Xt.Rows(1), Xt.Rows(2), Yt.Rows(1), Yt.Rows(2), Xisk)
Else
If Xisk >= Xt.Rows(Xt.Count - 1) Then ' Экстраполяция ЗА и интерполяция ПОСЛЕ второй известной точки - линейна
kus_interp_Ex = linterp(Xt.Rows(Xt.Count - 1), Xt.Rows(Xt.Count), Yt.Rows(Xt.Count - 1), Yt.Rows(Xt.Count), Xisk)
Else ' Между ними считаю по интерполяции полиномом с расположением заданного икса между двух пар точек
For i = 3 To Xt.Count - 1
If Xisk < Xt.Rows(i) Then
xd(1) = Xt.Rows(i - 2): xd(2) = Xt.Rows(i - 1): xd(3) = Xt.Rows(i): xd(4) = Xt.Rows(i + 1)
yd(1) = Yt.Rows(i - 2): yd(2) = Yt.Rows(i - 1): yd(3) = Yt.Rows(i): yd(4) = Yt.Rows(i + 1)
Linia_trenda yd, xd, 3, cd
kus_interp_Ex = cd(1) * Xisk ^ 3 + cd(2) * Xisk ^ 2 + cd(3) * Xisk ^ 1 + cd(4)
Exit For
End If
Next i
End If
End If
Case Else
End Select
End Function
======Входные данные:
Xt - Столбец исходных Х
Yt - Столбец исходных Y
Xisk - X при котором требуется определить Y
toch - количество используемых точек при интерполяции.
Наблюдательный заметит, что в макросе присутствует и интерполяция с использованием 3-х точек. (0_о)
Дополнительная функция, требуемая для макроса кусочной интерполяции - определение коэффициентов полинома линии тренда:
======
' Проведение интерполяции с использованием функционала Excel
' На выходе - коэффициенты полинома. Число точек должно быть минимум на одну больше, чем степень полинома.
' Данные берутся из программы
Public Sub Linia_trenda(ByRef Y() As Double, ByRef x() As Double, ByVal PolyStep As Integer, ByRef c() As Double, Optional ByRef r2 As Double)
Dim stepen As Long
' Ввожу проверку не превышения степени массива
If (UBound(Y) - LBound(Y) - 1) < PolyStep Then
stepen = UBound(Y) - LBound(Y)
Else
stepen = PolyStep
End If
' Объявляю переменные, создаю матрицы под размер данных и степень полинома.
Dim X1() As Double, Y1() As Double
ReDim X1(LBound(Y) To UBound(Y), 1 To stepen) As Double
ReDim Y1(LBound(Y) To UBound(Y), 1 To 1) As Double
ReDim c(1 To stepen + 1) As Double
' Заполню массив Х в соответствии со степенью уравнения.
For i = LBound(x) To UBound(x)
Y1(i, 1) = Y(i)
X1(i, 1) = x(i)
For N = 2 To stepen
X1(i, N) = X1(i, 1) ^ N
Next N
Next i
' Нахожу уравнение.
Dim Coefs As Variant
Coefs = WorksheetFunction.LinEst(Y1, X1, True, True)
' Вытаскиваю коэффициенты полинома.
For i = 1 To stepen + 1
c(i) = Coefs(1, i)
Next i
' Вытаскиваю величину достоверности апроксимации.
r2 = Coefs(3, 1)
End Sub
======Макрос linterp был представлен в прошлый раз.
Одним из замечательных применений кусочной интерполяции является возможность автоматического создания макросов функций без проблем с невозможностью достоверной апроксимации исходных данных вот в таком виде:
' Поправки Сербия Панчево Страница 39 из 77
Public Function ТЭХ_ПТ80_Рис3(ByRef Go As Single) As Variant
Dim Xt As Variant
Dim Yt As Variant
Xt = Array(13.0042194092827, 13.4767932489451, 14.0675105485232)
Yt = Array(-6.38888888888889E-02, -6.38888888888889E-02, -0.06875)
ТЭХ_ПТ80_Рис3 = kus_interp(Xt, Yt, Go, 4, 2)
End Function
Учтите что kus_interp при использовании данных с листа и из макроса отличаются...
Но об этом в следующий раз.
===========================
Планы на будущее
1. Часть 7. Автоматическое создание макроса функции с использованием кусочной интерполяции.
2. Построим поиск решения.
3. Строим график функции.