Парадокс Монти Холла получил свое название от ведущего телевизионного шоу "Let's Make a Deal". Игровая ситуация:

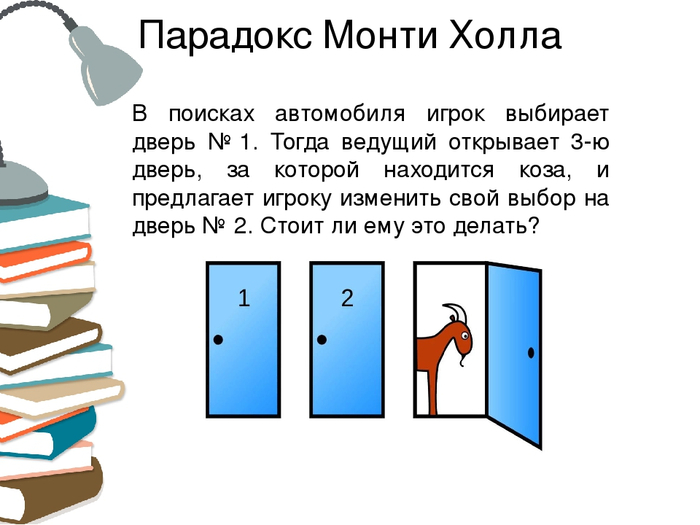
Перед игроком три двери, за одной из которых приз. Игрок выбирает одну из них, не открывая. После этого ведущий, открывает одну из двух оставшихся дверей. Ведущий знает, за какой из дверей приз, и всегда открывает дверь, за которой приза нет. Далее игроку предлагается поменять первоначально выбранную дверь на другую, остающуюся закрытой. Вопрос: повышаются ли шансы игрока при изменении выбранной двери?

Парадокс заключается в том, что интуитивно кажется, что смена двери ничего не дает. Приз либо за одной дверью, либо за другой. Ситуация симметричная, и вероятности одинаковы. Однако, теория вероятностей показывает, что смена двери повышает шансы выигрыша в два раза.

И с одной стороны так и есть. Если представить, что за дверьми находятся нули и единица, то вроде бы процент оставшейся двери увеличивается.

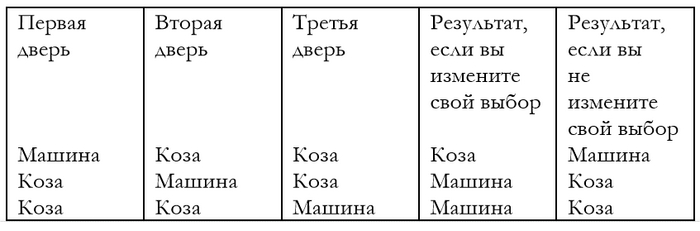
Три двери, первая верная, вторая и третья - неверные. Возможны три сценария:

1)Ты выбрал первую дверь, вторую убрали, при смене выбора ты проиграешь.

2)Ты выбрал вторую дверь, третью убрали, при смене выбора ты выиграешь.

3)Ты выбрал третью дверь, вторую убрали, при смене выбора ты выиграешь.

Но не кажется ли вам странным, что если дверей 1000, открыли 998, то почему-то у первой выбранной двери процент стремится к нулю

написал программу на си, где процент выигрыша при данном методе действительно 67.

у нас есть три двери. с нулями и единицей. выбранную рендомом дверь мы обнуляем, так как эту дверь по принципу Монти-Холла мы игнорируем. смотрим, осталась ли за дверьми единичка простым сложением. если осталась, то суммируем данный цикл +1.

в итоге просто смотрим процент этого парадокса

#include<stdio.h>

#include <stdlib.h>

int main()

{

    int sum,i;

    float sum2=0;

    int a[]={0,0,1};

    for (i=0;i<10000;i++)

    {

        a[rand()%3]=0;

        sum=a[0]+a[1]+a[2];

        if (sum>0)

            sum2+=1;

        a[0]=0;

        a[1]=0;

        a[2]=1;

   

    }

    //printf("Welcome to Online IDE!! Happy Coding :)");

    printf("Welcome to Online IDE!! Happy Coding %f\n)", sum2/100);

    return 0;

}

теперь добавил к программе тот факт, что каждый цикл двери меняются местами

#include<stdio.h>

#include <stdlib.h>

int main()

{

int sum,i;

float sum2=0;

int a[]={0,0,1};

for (i=0;i<1000000;i++)

{

a[rand()%3]=0;

sum=a[0]+a[1]+a[2];

if (sum>0)

sum2+=1;

a[0]=rand()%2;

a[1]=rand()%2;

a[2]=rand()%2;

if (a[0]==1)

{

a[1]=0;

a[2]=0;

}

else if (a[1]==1)

a[2]=0;

}

//printf("Welcome to Online IDE!! Happy Coding :)");

printf("Welcome to Online IDE!! Happy Coding %f\n)", sum2/10000);

return 0;

}

получилось около 58%. но так как рендом в си кривой и мои руки тоже, то где-то может быть обшибка. может кто-то перепишет с прямыми руками

пы.сы. если подкидывать монетку 20 раз, где 15 раз выпал орел, это всего лишь значит что монетка кривая, никак иначе

Весьма удивленные инертностью некоторых паттернов человеческого разума, исследователи Джулия Шредер и Уолтер Хебрансон решили проверить результаты на голубях, которые оказались ранее весьма успешными в ряде практических вероятностных задач.

Птицы и в этот раз не обманули ожиданий. После определённого обучения голуби эмпирическим путем научились выбирать правильную стратегию, а люди с таким же опытом — нет.

Вот как это было. Ученые отобрали шесть обыкновенных синих голубей и дали каждому на выбор три светящиеся кормушки. Последовал первоначальный отбор клювом, три кормушки погасли и после небольшого перерыва снова засветились две, из которых голубь сначала выбрал одну. Компьютерное моделирование заменяло Монти Холла, удаляя пустую кормушку.

После чего испытуемый снова мог выбирать между двумя оставшимися кормушками.

Призом была еда и, когда голубь правильно угадывал кормушку, она открывалась и птица получила награду. Этот выбор и награда, которую получал голубь в случае успеха, усиливали стимул и давали толчок к обучению. Затем появилось новое трио светящихся кормушек.

Птицы быстро научились делать правильный выбор, «рассчитывая» свои шансы, и в течение 30 дней процент смены кормушек увеличился с 36,33% до 96,33%. Некоторые птицы достигли абсолютных показателей: они всегда меняли свой выбор.

С людьми получалось иначе. В течение 30 дней экспериментов сначала наблюдался прогресс, но выявить тенденцию не удалось. Наблюдаемое увеличение изменения выбора увеличилось с 56,67% до 65,67%. Однако пределы доверительного интервала указывают на то, что выбор мог быть обусловлен случайностью.

Была проведена еще одна серия испытаний, в которых условия дилеммы Монти Холла ставились таким образом, чтобы было выгоднее придерживаться первоначального выбора. Цель состояла в том, чтобы проверить способность мозга находить оптимальные стратегии даже при внезапном изменении условий. Во втором эксперименте местоположение приза не было зафиксировано до тех пор, пока не был сделан первоначальный выбор.

Результат подтвердил тенденцию. Центральный процессор голубиного мозга все просчитал правильно. С первого дня неверная стратегия применялась в 30,17% случаев, в последний день (15-й) – только в 4,33% случаев. Различия среди молодых гомо сапиенс были незначительными: в первый день они изменили свой выбор в 30% случаев, в последний день в 27,67%.

Так называемая дилемма Монти Холла — известная загадка, названная в честь первого телеведущего американского шоу «Давай заключим сделку» («Let's Make a Deal»).

В этом игровом шоу он дал участникам на выбор три двери, одна из которых скрывает машину, а две другие скрывают за собой коз. Автомобиль и козы были расставлены заранее случайным образом и не меняли местонахождение.

После того, как участник делал свой выбор, ведущий всегда открывал одну из двух оставшихся дверей, за которой, как он знал заранее, не было машины. Затем кандидат имеет право открыть дверь, которую он изначально выбрал, или открыть третью дверь.

На самом деле у Монти есть несколько возможных стратегий, например, такие:

Адский Монти: Ведущий предлагает изменить свой выбор, если дверь правильная.

Ангельский Монти: ведущий предлагает изменить свой выбор, если дверь не та.

Козлиный Монти : с самого начала игры ведущий выбирает одну из коз и открывает её, если игрок выбрал другую дверь.

Поэтому предпочтительнее полагаться на не двусмысленную постановку задачи, включая ограничения, описанные Мюзером и Гранбергом следующим образом:

Рассмотрим три двери, одна из которых скрывает машину, а две другие — козу. Призы распределяются равномерно и случайным образом.

Ведущий знает распределение призов.

Игрок выбирает одну из дверей, но ничего не открывается.

Ведущий открывает еще одну дверь, не скрывающую за собой машину.

Ведущий предлагает участнику игры изменить свой выбор открываемой двери.

Ведущий никогда не открывает дверь, за которой стоит машина, поэтому, если игрок выберет дверь с козой, ведущий откроет единственную другую дверь с козой. А если игрок выберет дверь, за которой находится машина, ведущий случайным образом откроет одну из двух дверей с прячущимися за ними козами (возможно, ранее определённую жребием).

Тогда возникает вопрос: «Повышает ли игрок свои шансы выиграть машину, изменив свой первоначальный выбор?», иначе говоря: «Вероятность выигрыша при смене двери больше, чем вероятность выигрыша без смены двери?»

Подавляющее большинство игроков и респондентов отказались изменить свой выбор, хотя это удвоило бы их шансы на победу. При этом люди думают, что с оставшимися двумя дверьми шансы на победу равны и менять свой выбор нет смысла. Если вы думаете так же, не смущайтесь, потому что вы не единственный, кто обманывает себя.

Ниже приводится перевод известной формулировки данной задачи, взятой из письма, опубликованного Крейгом Ф. Уитакером в колонке «Спросите Мэрилин» от Marilyn vos Savant в журнале «Parade» в сентябре 1990 года:

Предположим, вы находитесь на съемочной площадке игрового шоу, стоите лицом к трем дверям и вам нужно открыть только одну из них, зная, что за одной из них находится машина, а за другими — две козы. Вы выбираете дверь, скажем, номер 1, и ведущий, который знает, что находится за каждой дверью, открывает другую дверь, скажем, номер 3, при открытии которой появляется коза. Затем он спрашивает вас: «Вы хотите открыть дверь номер 2?». Хотели бы вы изменить свой выбор?

Публикация данной статьи в журнале оказала немедленное влияние на читательскую аудиторию и вызвала бурную дискуссию среди математиков, известных или нет, и анонимных любителей. Таким образом, Мэрилин вос Савант получила более 10 000 писем. Как видите, троллинг процветал даже в те времена, когда приходилось тратить гораздо больше сил и времени, чем сегодня, да ещё и платить за почтовый конверт и почтовую марку. А статья оказалась в тех ещё трендах!

По слухам, талантливый венгерский математик Пауль Эрдёш тоже попал в ловушку и даже отказывался принимать решение, пока своими глазами не увидел компьютерную симуляцию результатов эксперимента. Честно говоря, в это трудно поверить, но такой слух все же существует.

Для выигрышной стратегии важно следующее: если вы меняете выбор двери после действий ведущего, вы выигрываете, если изначально выбрали проигрышную дверь. Это произойдет с вероятностью 2/3, потому что изначально вы можете выбрать проигрышную дверь 2 из 3 способов.

Но часто при решении этой задачи люди рассуждают примерно так: ведущий всегда убирает проигрышную дверь, тогда шансы на появление автомобиля за двумя не открытыми дверями становятся равными 1/2, независимо от того, какой был первоначальный выбор. Но это неверно: хотя вариантов выбора действительно два, эти варианты (в контексте) не равновероятны. Это так, поскольку изначально все ворота имели равные шансы на победу, но затем были исключены разные вероятные события.

У большинства людей этот вывод противоречит интуитивному восприятию ситуации. Из-за возникающего несоответствия между логическим выводом и ответом, к которому склоняется интуитивное мнение, задача называется парадоксом Монти Холла.

Ситуация с дверями становится немного более очевидной, если представить, что изначально дверей было не 3, а, скажем, 1000, и после выбора игрока ведущий убирает 998 из них, оставляя только 2 двери: ту, которую выбрал игрок, и еще одну. Тогда кажется более очевидным, что вероятности найти приз за этими дверями различны и не равны 1/2. Если мы изменим выбор двери, мы проиграем только в том случае, если сначала выберем дверь, за которой была машина, вероятность чего 1/1000. Мы выиграем, если наш первоначальный выбор был неправильным, и вероятность этого равна 999 из 1000. В случае 3 дверей, мы должны пользоваться той же логикой, но вероятность выигрыша при изменении решения соответственно будет 2/3, а не 999/1000.

Испытали ли вы когнитивный диссонанс, пытаясь понять этот парадокс?