pencilTM

Все знают про "косой косил косой". Про зайца.

Если по максимуму использовать слово "косой", то может получится такая абракодабра.

"Косой косой с косой косил косой косой на косе"

Не люблю крайностей. И в эти дрязги невротиков никогда не вступаю. Людям с пограничным состоянием всё равно за кого топить, куда их прибьёт течением, с того берега они и орут, кидаются камнями, плюют.

Вот давайте посмотрим на картинки, а потом прочитаем анамнез специалиста.

Итак картинки (модераторы! где красивая толстая красная линия?):

А теперь послушаем, что скажет собаковод:

Эти фотографии принадлежат девушке (не из России), которая подобрала собаку с улицы и решила сделать с ней фотосессию. Неизвестно, сколько прошло времени от «подбирания» до фотосессии, но судя по реакциям собаки на девушку – немного.

Вероятно, вам сейчас очень захочется написать злой комментарий. У одних людей появится сильное желание обвинить девушку в отсутствии «элементарных» знаний о собаках, их языке тела, технике безопасности и так далее. У других появится не менее сильная злость в адрес собаки, которая «не должна кусаться», и будет желание написать о том, что таких собак быть не должно.

Это нормальная защитная реакция психики на столкновение с чем-то угрожающим и непонятным.

Даже меня побуждает написать эту публикацию страх. Но за счет того, что я очень хорошо понимаю, ЧТО произошло на этой фотосессии и ПОЧЕМУ собака укусила – я не испытываю желания никого обвинить.

Девушка НЕ виновата, что у нее не было на тот момент нужных знаний и опыта.

Собака НЕ виновата, что она не доверяет чужому человеку и не понимает его намерений.

Это несчастный случай. И пусть он никогда и ни с кем не повторится.

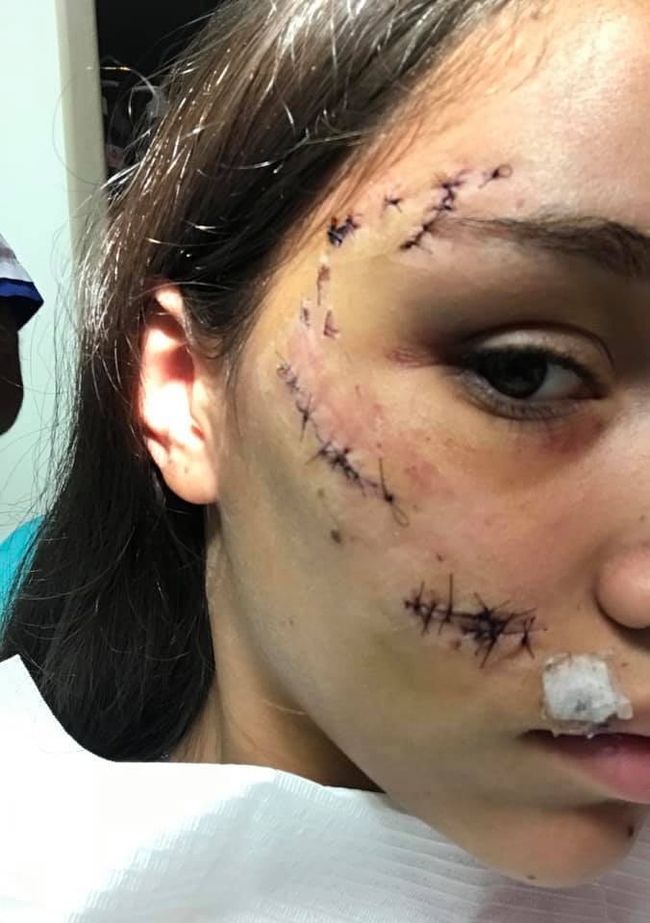
Итак, что можно увидеть на первых фото?

1. Собака отклоняется от девушки, прижимает голову к полу, сильно напряжена. Фото с «улыбкой» собаки обманчиво – да, пасть раскрыта, но тело напряжено, а значит, собака НЕ расслаблена.

2. Отведенные назад уголки губ и раскрытая пасть при общем напряжении тела обычно свидетельствуют о гипервентиляции легких. Так как собака не испытывает серьезных нагрузок, то это либо перегрев, либо стресс от непонимания ситуации.

3. Основание хвоста на обоих фото прижато – собака очень неуверена в себе, ей некомфортно, она опасается.

Из этого можно сделать вывод, что собака не доверяет девушке, не понимает ее, возможно, ей к тому же жарко и она устала.

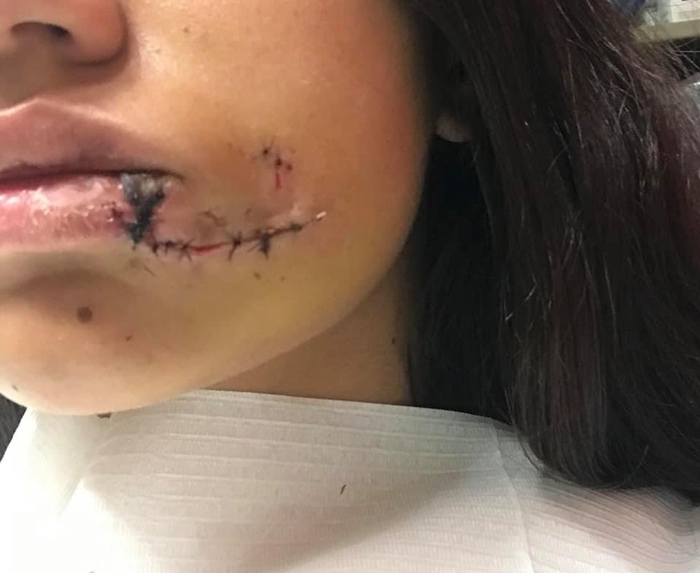
Третье фото с укусом:

1. Укус пришелся на ближайшую точку к собаке – за лицо девушки, обнявшей собаку за шею.

2. Вероятный вывод – девушка обняла собаку и навалилась на нее сверху, что было воспринято собакой как угроза/нападение на пустом месте.

3. Зубы собаки очень неудачно касаются виска, щеки и противоположной щеки, что при даже не очень сильном смыкании челюстей приведет к рваным ранам.

Четвертое и пятое фото с последствиями укуса:

1. Четкие чистые «порезы» на лице девушки показывают, что укус был однократным, не очень сильным (собака не сжала челюсти).

2. Такой укус называют «удар зубами». Собака распахивает пасть, бьет зубами и отступает. Равносильно нашему, человеческому, толчку или хлопку рукой, это попытка защитить себя без серьезного конфликта.

3. Человеческая кожа, в отличие от собачьей, плотно прилегает к мышцам, из-за чего ЛЮБОЙ укус собаки, даже в игре, может сильно повредить ее.

4. Укус собаки во время самозащиты рассчитан по силам и жесткости на ДРУГУЮ СОБАКУ, а не на человека. Собака в состоянии фрустрации, как на этих фото, не может рассчитывать свои силы (люди, кстати, тоже с этим плохо справляются). Она кусает так, как укусила бы другую собаку.

5. К сожалению, любой собачий укус за лицо человека приводит к травмам мягких тканей. Чаще всего к рваным ранам, что мы и видим на фото.

Что нужно знать, чтобы подобного никогда не произошло?

1. Нужно научиться видеть/чувствовать сильное напряжение собаки во время тактильного контакта и не лезть в это время к ней лицом. Это просто техника безопасности. Например, не надо ложиться лицом на разделочную доску, когда любимый человек в раздраженном состоянии режет на ней что-то ножом.

Собака может напрячься просто потому, что ей щекотно и у нее ощущение ползущего насекомого на ноге. Она отмахнется туда зубами – а там ваша щека.

2. Не надо в принципе лезть лицом и обнимать малознакомых вам собак, если вы не умеете читать их язык тела. Хотите обниматься с чужими собачками – не вопрос. Пригласите их подойти и если они сами идут обниматься, тогда и обнимайте. Если собака отстраняется – отпустите. Незнакомая или малознакомая вам собака это НЕ ВАША собака.

3. Если вы взяли взрослую (старше 8-10 ти месяцев) собаку с улицы, из приюта, от других людей – не важно породистая она или беспородная, большая или малюсенькая – она вам ЧУЖАЯ. И вы для нее тоже чужие! На установление даже первичной привязанности нужно не менее 2х недель.

То, что собака ходит хвостом и лезет на руки не значит ровным счетом ничего – она просто пытается выжить в новых условиях с помощью привычной программы поведения. На установление полноценной привязанности даже лабрадору из хороших условий нужно не менее 2х месяцев. А кавказской овчарке из плохих условий может потребоваться год и даже больше.

4. Доверие не равно привязанность! Собака может вас обожать, выделять вас из всех людей, следовать за вами, слушаться. И не доверять. Совсем – или только в определенных условиях. Например, при тесном тактильном контакте. А недоверие строится на непонимании вашего поведения и его последствий, на невозможности вас предсказать и предугадать, что вы будете делать.

Если собака была в плохих условиях или сталкивалась неоднократно с непредсказуемым поведением людей, то ее доверие иногда приходится завоевывать ГОДАМИ.

5. Нет, собака не благодарна, что ее взяли с улицы. Конечно, когда есть еда, вода, убежище – это лучше, чем скитаться и голодать. Но если вы приняли такое решение спасти собаку, то это ваше решение, а не ее.

Она может пойти за вами, потому что вы похожи на ее прежних хозяев или на доброго человека покормившего на прошлой неделе. Но она не может знать, что ее ждет – хорошее отношение или привязь и побои. И как бы вы не хотели позаботиться о ней, старайтесь напоминать себе, что это вы решили взять эту собаку. Она не просила. Она просто хотела ласки и поесть, в лучшем случае. А не «этовотвсе».

Что делать, чтобы такого не произошло?

Есть три «лекарства»: страх, доверие и обучение.

Последние два, кстати, помогают друг другу.

1. Страх. Если собака боится, она с меньшей вероятностью будет защищать себя. Но зато всегда есть вероятность агрессии страха, когда собака начинает драться, как загнанная в угол крыса, не думая уже о собственной безопасности.

В отличие от самозащиты, когда собака откусывается и старается сразу отойти в сторону, при страхе укусы всегда множественные, жесткие и страшные, потому что собака в панике не контролирует себя. Если бы собака на фотографиях укусила девушку от страха – ее лицо пришлось бы собирать по частям.

2. Доверие. Если собака доверяет вам (а на это нужно время и предсказуемость вашего поведения для собаки), то она просто знает, что тактильный контакт, даже если он ей неприятен, не несет угрозы. При доверительных отношениях собака готова многое стерпеть. И постепенно учится все спокойнее переносить даже неприятные крепкие объятия и поцелуи в нос.

3. Обучение. Если собака обучена, что тактильный контакт выгодная штука, за которую она получает то, что хочет, - у нее просто нет причин защищаться. И чем больше вы работаете над выгодным для собаки контактом, тем выше доверие к вам, так как ваши действия становятся предсказуемыми и приятными. В этом случае собака уже не просто терпит, а может начать радоваться объятиям и поцелуям.

Выводы:

🔴 У собак есть зубы, и они могут причинить человеку намного больший вред, чем другой собаке.

🔴 Собаки защищают себя, если не доверяют и не понимают намерений человека.

🔴 Усталость, дискомфорт, стресс – увеличивают вероятность и силу укуса.

🔴 Собака остается чужой, пока между ней и человеком не образовалась привязанность.

🔴 Если вы не научили собаку доверять чужим людям – она не будет им доверять. Потому что они чужие.

🔴 Лезть лицом и обнимать чужую собаку, которая этого не хочет – всегда плохая идея, чреватая последствиями и для вас, и для собаки.

Юлия Исламова

Девушка достаточно подробно всё описала - должно стать понятным даже самым непонятливым.

От себя добавлю. Где-то прочитал, что собаки не любят ласк, тактильного контакта самого по себе. Мы, обезьяны, воспринимает тактильный контакт, положительно, для нас, нашей психики это успокаивающие, ласкающие воздействия. Собаки же разного рода обнимашки изначально терпят, т.к. у них есть "личное пространство". И нарушить это пространство может не каждый. Если она доверяет нарушающему, то разрешает нарушать без стресса для себя.

У меня был амстафф. Да, они просился на ручки (на колени), ему было уютно. И когда чешешь "подмышки", брюшко, он (и не только он) ложился на спину, подставляя самое уязвимое место.

Но всё это происходит не стразу. И любая собака стрессует в новых условиях. Пока не убедится, что окружающие её люди не наносят ей вреда и ожидать иного от них не приходится.

И ещё одна выдержка - пара комментов под перепечаткой статьи.

В детстве меня укусила дворняжка. Ну, как укусила, прикусила, тоже за лицо.
Гуляла на детской площадке, там местная дворняга жила, кобель старый. Мама ела мороженное и болтала со знакомой, пес сидел напротив нее и заглядывал в рот. Мне было лет 6 может, 5. Без особого размышления, как обычно я подошла к Рыжику сзади и обняла его за шею. Рефлекторно Рыжик поднял голову и цапнул. Цапнул он не сильно, в силу возраста может, или стертых зубов, не суть. Остались царапины. В итоге получила еще люлей от мамы, и мы пошли промывать раны домой. Кстати, пес этот с тех пор меня опасался, не подпускал больше к себе, пытался скалиться. Было пару попыток в его расслабленном состоянии, но тщетно. Больше я его и не трогала.
И только спустя еще лет 8, когда я начала изучать зоопсихологию, я начала винить в этом случае себя, а не "внезапно злого Рыжика".
К слову, страха перед собаками после этого я испытывать не стала, совершенно спокойно перенесла данную ситуацию, может даже чуть-чуть поумнела) Хотя, после этого еще кусали несколько раз, уже в более взрослом возрасте. И там-таки виновата опять была я сама, во всех ситуациях. Ниче, ниче, опыт, опыт)

Вот вообще не согласен с текстом в начале статьи, но автора можно понять... у нас слишком толерастное общество и очень легко "кого-то обидеть"))) даже сейчас уже наверное, кто-то обиделся)))
Виновата девушка ОДНОЗНАЧНО!!! Более тупой идеи, как устроить фотосессию с незнакомой уличной собакой представить трудно!!! Собака еще ангел - долго продержалась судя по существование первых двух фото.
И еще забыли кое о ком, кто тоже имеет место быть в этой истории и виноват не меньше этой укушенной. Это фотограф!!! Если у твоего близкого, друга, знакомого нет мозгов вообще, так помоги ему. Хотя-бы попытайся отгородить от фатальной глупости!

Да, человек отличается от других животных потенциальной возможностью думать, анализировать и делать выводы. Но не все этой потенцией пользуются.

И ещё пара слов о стаях бездомных собак в городах.

Собака в принципе не приспособлена жить в дикой природе. Собаки отличаются от волков тем, что они всегда остаются "щенками", "детьми", они не взрослеют, не становятся самостоятельными психологически. Да, и еду себе они не умеют себе добывать.

Получается, что те, кто выбрасывает собак на улицу, наигравшись и натешивши своё эго, по сути дела, выбрасывают на улицу беспомощных детей, полностью зависящих от человека. А те уже сбиваются в стаи и ведут себя как маленькие беспризорники, уже не ожидающие от двуногих лысых обезьян чего-то хорошего.

Вы же злитесь на внезапный дождь или град - такова наша среда. И беспризорные собаки тоже наших рук дело. Да, если нет возможности пристроить собак и нет возможности по-человечески их содержать в приютах, то лучше усыпить. Не мучить ни их, ни подвергать опасности себя и  детей.

Ещё одна цитата из комментов:

Такие раны собачьи зубы оставляют исключительно при стаскивании собаки с схватки. Она режет клыками плоть не разжимая зубов.

По всей видимости девушка испугалась и в панике резко одернула голову, тем самым по сути распоров себе лицо о собачьи зубы, даже если собака просто прихватила, такое поведение ведет к глубоким травмам.

Поднесите руку к гвоздю насквозь пробитому в заборе, прижмите руку, чтоб острие продавило кожу, а затем одерните не на себя, а проведите им по коже с таким же давлением. Результат будет как на фото.

начало здесь Логарифмические чувства и их производные

Решив освежить в памяти цифры числа е после запятой, полез в Вики. Воодушевившись замечательными свойствами этого числа, бросил взгляд на те самые циферки после запятой, ради чего и залез в статью (кстати, "7" не забывается, а вот для следующих циферок в статейке обнаружилась интересная подсказка - два раза по 18 28).

Чувство Прекрасного и Жажда поиска Гармонии и всеобщих взаимосвязей между законами и явлениями этого бренного физико-химико-биологического мира, тут же обратили моё внимание на 271. "Знакомое число", - обменялись они взглядами. "И где же оно могло нам встречаться?"

Да, это та самая температура 0°С, при которой стынет кровь в жилах вода в проруби (и не только в проруби). Выраженная в градусах Кельвина. Ну, почти. В Кельвинах она будет 273. Но ведь почти в яблочко!

А что такое наше число е? Да это и есть соотношение. Ведь в нашем мире всё не на сколько-то, а во сколько-то раз больше или меньше, сильнее или слабее, светлее или темнее...

И температура ничем в этом плане не отличается от звука, который принято измерять в дБ, т.е. относительных величинах. Например, если мы сравниваем температуры плавления металлов, то относительные величины нам скажут больше, чем абсолютные температуры. Тем более удобнее это делать в Кельвинах, чем по шкале Цельсия (больше предназначенной для быта).

(кстати, заметьте, что авторы статьи, откуда взята картинка с температурами плавления, привели проводимость (обратная величина к сопротивлению) металлов в относительном виде.)

Прежде чем самостоятельно логарифмировать температурную шкалу (чтобы посмотреть, что получится - чисто из любознательности) по красивому основанию Эйлера-Непра, решил поискать на просторах инета данное решение - может хоть кто-то рассматривал данный (совершенно очевидный) вопрос с этой точки зрения. И... наткнулся на потрясающую статью, где подробно освещена и история вопроса.

--------------

Ликбез.

Существует несколько температурных шкал.

Температурная шкала Фаренгейта, в которой точкам замерзания и кипения воды соответствуют крайне неудобные числа 32 и 212°, была предложена в 1724 Г.Фаренгейтом. Шкала Фаренгейта широко распространена в англоязычных странах, но ею почти не пользуются в научной литературе.

Стоградусная шкала, где точке замерзания воды соответствует 0°, а точке кипения 100°. Называется шкалой Цельсия по имени А.Цельсия, шведского астронома, который описал ее в 1742.

Для перевода температуры по Цельсию (ОС) в температуру по Фаренгейту (OF) существует формула °F = (9/5)ОС + 32, а для обратного перевода формула ОС = (5/9)(OF-32).

Обе шкалы - как Фаренгейта, так и Цельсия, - весьма неудобны при проведении экспериментов в условиях, когда температура опускается ниже точки замерзания воды и выражается отрицательным числом. Для таких случаев были введены абсолютные шкалы температур с абсолютным нулём. Одна из них называется шкалой Ранкина, а другая абсолютной термодинамической шкалой (Кельвина); температуры по ним измеряются в градусах Ранкина (OR) и кельвинах (К). Обе шкалы начинаются при температуре абсолютного нуля, а точка замерзания воды соответствует 491,7° R и 273,16 К.

Т.е. Ранкин - это Фаренгейт со смещением, а Кельвин - это смещённый Цельсий. Градусы Цельсия переводятся в кельвины по формуле К = ОС + 273,16, а градусы Фаренгейта - в градусы Ранкина по формуле °R = °F + 459,7.

Что такое температура? Из энциклопедии известно, что латинское слово temperature означает "надлежащее смешение, нормальное состояние", а по науке - это "физическая величина, характеризующая состояние термодинамического равновесия системы".

Очень сложно, мало понятно и неудовлетворительно. Мудрейший Перышкин характеризовал температуру как "степень нагретости тела". Это ближе к жизни, здравому смыслу, логике бытия.

Однако, относительность оценки нагретости того или иного физического тела или физического процесса очень хорошо иллюстрировала Качество, но мало информировала о Количестве. До Возрождения большинство ученых мужей (физикусов по латыни) вполне обходилось в своих  философских и умозрительных трудах сравнительной температурой. Но с появлением мануфактур,  фабрик серийной продукции, появилась огромная потребность в абсолютном количественном измерении температуры, как степени нагретости, именно!

Металлургия, станкостроение и, наконец, паровая машина, потребовали точности измерения, достоверности сравнения, воспроизводимости достижения определенной ступени (градуса) температуры. Недогревы или перегревы изделий приводили к бедам, авариям и катастрофам.

Согласно современным историческим представлениям первую удачную температурную шкалу немецкий физик Габриэле Фаренгейт (1686-1736), работавший в Англии, предложил в 1724 году.

Фаренгейт предложил за 0 градусов принять температуру замерзания-таяния эвтектического водного раствора поваренной соли NaCl (это по привычной нам шкале Цельсия составляет -21,2°С). Почему? Да потому, что эту температуру легко воспроизвести может и домашняя хозяйка: жиже раствор - вымерзает вода, гуще раствор - выпадает соль, а остается всегда эвтектика, которая плавится и замерзает с приличной точностью одинаково, всегда и везде. Да и морозов в Гольфстримовой Англии сильнее не бывало.

В моду, в жизнь, в физику настойчиво "просилась" десятичная система и, будучи Ученым истинным, Фаренгейт предложил за +100 град. принять не что иное, как довольно стабильную температуру (степень нагретости) человеческого тела. Почему? Потому что гладиолусы да Царь Природы! Ну и у многих теплокровных животных температура тела близка была. Ведь тогда градусников, термометров, термовизоров еще не было, их еще надо было изобретать.

Так вот, предложив за 100 градусов температуру человеческого тела (+36,7 град. С), Габриэле Фаренгейт создал равномерную десятичную температурную шкалу по двум общеизвестным и хорошо воспроизводимым реперным точкам. Америка до сих пор пользуется шкалой Фаренгейта, а не общепризнанного Цельсия. Вспомните аляскинские книги Джека Лондона или "451 град. по Фаренгейту" великого Рея Бредбери. Да и практически морозов ниже 0 град. в Англии, США и иже с ними почти не бывает, а если наступают, то это очевидное (минус по Фаренгейту!!!) стихийное бедствие, закрытые школы и ограничение любой деятельности. Ведь северная граница США с Канадой проходит по широте нашего Краснодарского края! Можно считать -21.2 град. С страшным морозом.

Удобная, практичная и горделивая шкала Фаренгейта была не только первой, но и весьма далекой от Истины, хотя и на пути к ней.

Во Франции Рене Реомюр (1683-1737 г.г.) предложил в 1730 году свою шкалу температур, приняв за 0 град. Re температуру тройной точки воды (0 град. С), чем сделал огромный не шаг, а скачок к Истине, но Лукавый попутал французского физикуса и он, предложив за вторую реперную точку температуру кипения воды, присвоил ей 80 Re(?), оставив шкалу несколько неудобной и несколько недосказанной. Это и дало возможность Андерсу Цельсию (1701-1744 г.г.) уже в 1742 году войти во все энциклопедии мира и бытовые термометры на сотни лет, построив свою шкалу на 0 град. С в Реомюровой тройной точке воды, но кипению воды придав +100 град. С!!! Это было восхитительно, удобно, практично, наглядно и перспективно аж на 251 год.

Однако в физике, химии, механике и т.п. градусы Андерса Цельсия требовали сложнейшей алгебраической взаимосвязи, особенно при строительстве паровых машин. Шаг к Истине, но тоже далёкий пока.

Вторая половина XVIII века ознаменовалась выдающимся событием всех времен и народов: Человек впервые (официально и зарегистрированно) ПОЛЕТЕЛ!!! В 1783 году 21 ноября на тепловом воздушном шаре братьев Монгольфье на глазах десятков тысяч парижан перед Дворцом Короля два человека: ученый и аристократ всплыли в Небо, проплыли над Парижем и благополучно приземлились в пригороде. Это Чудо затмило еще большее чудо, которое произошло два месяца спустя: ученый Жак Шарль поднял в небо водородный аэростат, именно который стал родоначальником всех современных аэростатов, стратостатов и дирижаблей. А температура здесь при том, что этот же Жак Шарль в 1787 г. впервые напрямую связал два основополагающих физических параметра - Давление и Температуру!

(Давление газа в замкнутом объеме пропорционально температуре)

Он определил коэффициент ... Сейчас каждый [советский] троечник-восьмиклассник знает - это не точно, но двести двадцать лет назад?.. Шедевр! (*** сейчас и выпускник россиянского вуза этого не знает - прим.ТС)

Эстафету на пути к истине подхватил Гей-Люссак, построив изобарический, почти газовый термометр по объему газа...

Коэффициент О± Гей-Люссак определил равным 1/264. Это было уже в 1802 году. Все эти усилия осмыслить пытался шотландец Уильям Ранкин - тепловик, паровик, термодинамик... Он предложил в 1842 г. свой паровой цикл и свою шкалу температур с градусом больше, чем Цельсия: 1 град.Ra = 1,8 град.С. Эта шкала при температурах паровой машины позволяла проще связывать: объем, давление и температуру пара. Но до Истины было слишком еще далеко...

И вот в 1848 году английский физик Томпсон занялся уточнением коэффициента в формуле Гей-Люссака и построил график зависимости объема газа от его температуры:

Построив теорийный линейный график и "уложив" на него экспериментальные точки, господин Томпсон пролонгировал график влево и... Так был получен "Абсолютный нуль" температуры. Так был уточнен коэффициент Гей-Люссака О± = 1/275. Так была предложена новая шкала с 0 градусов в абсолютном нуле и 275 градусов в тройной точке воды. Так хитро была сохранена преемственность шкалы Цельсия, ибо градус (ступень) были выбраны те же. Это был прорыв к Истине, прорыв в гармонию!

Королева Великобритании и Королевское Научное Общество Англии были так восхищены красотой, простотой и наглядностью новой термодинамической шкалы г.Томпсона, что его ввели аж в состав пэров Англии и присвоили новое имя лорда Кельвина. Так родилась знаменитая термодинамическая шкала температур или шкала Кельвина.

Менделеев Дмитрий Иванович не остался в стороне и уточнил еще более коэффициент О±, и уже в семидесятые годы XIX века он стал равен 1/273, а абсолютные нуль - минус 273 град. С. Великие Клайперон и Менделеев сформировали знаменитую формулу, объединяющую параметры состояния идеального газа во всех условиях.

Однако... Однако вот уже лет сто пятьдесят существуют две независимые шкалы температур Цельсия и Кельвина, и ни та, ни другая не собираются уступать.

Весь быт, погода, жизнь описывают свою температуру в градусах Цельсия. Это наглядно, очевидно, практично. Ниже нуля температура: мороз, лед, холод. Огурцы, вишня, клубника пропадают, коли на 2-3 градуса ниже нуля. Заморозок! А 273,15К? Черти-чего. Абракадабра.

При 271К что? При 275К что? И вообще, хотя термодинамика все уточняет: сначала абсолютный 0 = -250°С; -264°С; -275°С; -273°С. А потом, с пятидесятых годов, стали уточнять уже не абсолютный нуль Кельвина, а обосновывать термодинамическую шкалу с одной опорной точкой: тройной точкой чистой воды. В сороковые годы нашего XX столетия приняли-утвердили ее в 273,15°К, а когда некоторые стали получать почти абсолютный 0, то в 1961 году Международный конгресс криогенщиков добавил соточку градуса, и температура тройной точки воды стала 273,16°К. Однако, и с этой точкой хитрые физики уже достигли Т = 0,000001К?! Вот лукавые. Ну и бог им судья, а я вижу выход из температурного тупика не в отдании предпочтения той или иной шкале, а в создании новой.

Новая шкала температур однозначно должна быть термодинамической и соответствовать уравнению идеального газа Клайперона-Менделеева, но так, чтобы убрать-поглотить универсальную газовую постоянную, превратив уравнение в "... элементарно, Ватсон!"

Но, это не температура Кельвина, а новая натуральная шкала температур.

Пожелание благое, но на какой основе и на каких точках опорных температур? Как уже говорилось: никаких революций! Вода как основа жизни, климата, биосферы планеты Земля, именно в температуре своей тройной точки есть для нас Истина. Вот и пусть останется своей и нашей основополагающей, опорной, базовой точкой натуральной шкалы, как у Реомюра, Цельсия, Кельвина: Одноопорная шкала! С другой стороны новая шкала должна быть еще более наглядной, удобной, практичной в быту, чтобы сопротивление консерваторов было минимальным.

Ну и с третьей стороны величина градуса, ступеньки, как бы кванта температуры, должно быть обоснованным и, не отрицая прошлого, породить новые свойства температурному Мировоззрению.

Корнем слов "случай", "случайность", "случайно" и т.д. является слово луч! Чей? Какой? "Кавойный"? Не нашего ума дело! Но еще хитрец Эйнштейн любил говаривать, что "Бог в кости не играет!" Отсюда выбор градуса, выбор величины температуры тройной точки воды, выбор очевидности недостижимости абсолютного нуля должны быть чем-то обоснованы.

Просто так ничего не бывает. И вот Однажды... Я, случайно, смотря который раз на эти 273,16 градусов, вдруг увидел в них нечто знакомое, родное и близкое, но что? Никак не выкристаллизовывалось довольно долго. Я ходил, жил да был, работал, ожидал, любил и ненавидел, но никак. Как глухая зубная боль... И только в Бюраканской обсерватории, где я был в командировке от Красногорского оптико-механического завода, услышав и разобравшись с физической сущностью реликтового излучения или микроволнового фонового излучения, до меня дошло или меня осенило...

Максимум интенсивности изотропнейшего фонового излучения Вселенной в коротковолновом (на сантиметровых, миллиметровых и сублимиллиметровых волнах) приходится на температуру 2,7 К! (cм. "Энциклопедию космоса" с.403, М., <Советская энциклопедия>, 1986г.) Да ведь это же число Непера, число "е", основание натурального логарифма... А тройная точка воды? Ведь это точно 100е! Ну не совсем точно, ведь принято, что она равна 273,16 К, а здесь получается 271,8281828:, что дает погрешность 0,49% Тем хуже для старой шкалы, и лучше для новой. Эврика! Ибо это погрешность шкалы Кельвина.

Значит так! Температуру стабилизированной тройной точки воды принимаем равной точно 100е новой натуральной шкалы температур, что составляет 271,8281828: градусов уточненной термодинамической шкалы температур Кельвина. При этом чтобы шкала на одной точке не качалась и не колебалась, принимаем, что максимум интенсивности вечного реликтового излучения приходится точно на 1 градус новой шкалы натуральных температур, что по новому лорду Кельвину составляет точно 2,718281828:! Проведя новую прямую температурной шкалы Кельвина, мы увидим, что один край ее мы приспустили (на 0°С, почти на 1,33°К), а другой край у 2,7°К приподняли почти на две десятых... Это означает, что абсолютный нуль чуть отъехал дальше, а значит и нобелевские потрудней станет получать.

Мне стало страшно! Это что, я умней всех? Да нет, конечно. Просто Муза посетила: А вдруг блеф или "много шума из ничего"? Я стал считать, проверять и сравнивать. Будучи криогенщиком по образованию, энергетиком по воспитанию и изобретателем по призванию я "пробовал на зубок" все, и вот выводы:

1. Более шестнадцати известных физических природных процессов довольно прилично описываются экспоненциальной зависимостью: "е" в степени;

2. Реперные температуры (опорные точки), общепринятые сегодня для градуировки термоднамической шкалы не имеют в градусах Кельвина ни одной целочисленной величины, а в натуральных градусах...? Не десять, не "π", не 3, а именно "е"!

Совпадение? Случайность? Закономерность!!!

3. Почему именно число "е" обладает такими чудотворными свойствами мне, по великой Милости Божей ясно, но об этом пока рано громко говорить, пусть каждый читатель попробует "на зубок" число "е", да заодно число "π", может чего и откроется. На этом у многих "пифагорийцев" за три тысячи лет "крыша поехала".

Подскажу одно, что = 9,8696:, а такую величину в "СИ" Земля имела всего несколько миллионов лет назад?! И "воще"...

4. Градус, ступенька, уступчик натуральной шкалы стал больше, проще, четче и... бесконечнее до иррациональности. Помните: "Электрон также неисчерпаем, как Земля"?!!!

5. Гениальный Дмитрий Иванович Менделеев в 1873 году предложил новый, метрический градус, равный 0,2728 град. (а это значит в метрической шкале температур тройная точка воды равна была бы 1000 градусов. Почти точно), а это ясно мне теперь, что градус метрической равен

е/10 = 2,7182818/10 , т.к. 1 кГс = 9,81...Н!

Дмитрий Иванович не ошибся, потому что его градус был равен "изменению температуры, при котором давление газа (у Менделеева - водорода) увеличивается на 1 ата". Вот это откровение! Жаль, что Дмитрий Иванович не узрел в своей величине числа Непера: А может и узрел, но помалкивал? Ведь весь научный, цивилизованный и просвещенный мир так до сих пор ревниво не простил русскому открытие "Периодической системы элементов".

На западных таблицах нет ни фото, ни имени, ни родины автора величайшего открытия XIX века.

Подумаешь" Случайно, нечаянно, приснилось. И Нобелевскую зажали, и открытие критических температур веществ увели, и шкалу метрическую умолчали!

6. А простота, наглядность и очевидность шкалы Цельсия? Очень похоже это и у шкалы натуральных температур. Больше 100е - тепло! Меньше 100е - мороз! Да и каждый градус (2,713°С, °К) физически осязаем отличим и ощутим.

А температура человеческого нормального тела? Она равна ровно 114е или 36,734°С. Это точнее! Сто пятнадцать - 39,45°С? Срочно спасать! Сто тринадцать - 34,01°С? Жуткий упадок сил - в реанимацию!

В общем новая предлагаемая шкала натуральных температур много ближе к Истине, чем шкала Кельвина. Она также удобна, практична и очевидна, а может и больше, чем шкала Цельсия. Кроме того, бесконечность каждого градуса - ступени в виде числа "е" градусов, уточненной термодинамической шкалы температур лорда Кельвина, имеет свое физическое, энергетическое, экологическое и, даже, философское содержание.

Но про философию... это тема уже другой статьи.

Р.S. В 1987 году я поделился со своим другом, ученым В.Д.Шабетником этими мыслями и предложениями. Он, осмыслив их и связав новую шкалу температур с квантовыми свойствами субатомных частиц элементов периодической системы Менделеева, сумел обнаружить Закономерности температур кипения и Закономерности изменения энергии при нормальном кипении - конденсации газов. Мы с ним авторы двух заявок на открытия №579 и №580: Но это уже другая статья. Например, в газете "Не может быть" №6 за 1993 г.

Инженер А.Рубайло

ну, согласитесь, классное предложение! И переходить на такую шкалу проще простого.

Что такое математика? Все мы когда-то в детстве ковырялись в песочнице с совком и строили замки из песка. Чуть позже копали лопатой ямки под посадку деревьев или вскапывали поле под картошку. Кто-то затем освоил профессию экскаваторщика.

И математика – это такой же инструмент. Все мы пользуемся «детсадовским совком» при расчётах в магазине – сложить, отнять, умножить, поделить. Кому-то пригодилась и «математическая лопата», например, при планировке и постройке дома или сарая на даче или загородном доме. А кто-то освоил и «математический экскаватор», пойдя в математики.

Но абсолютное большинство, если и не знает значения, но помнит такое слово, как «логарифм». Некоторые даже знают его «сестру» экспоненту.

- Зачем нам все эти логарифмы и экспоненты в повседневной жизни? – спросит читатель.

Как ни странно, но и люди воспринимают окружающий мир «логарифмически» и природные процессы протекают «логарифмически», хоть и создаётся впечатление, что мы живём в линейном мире, в линейном пространстве, линейном времени. Вроде везде у нас линейные измерения – метры, секунды, сила тока, сила света, сила тяжести, температура… Кстати, о последней в конце рассказа.

Хоть нам и кажется всё линейным (т.е. измеряемым просто «линейкой» или другим прибором с равномерной шкалой), однако же мы ежедневно пользуемся нелинейными приборами (и нелинейными чувствами, точнее, сенсорами), не замечая этого.

Небольшое отступление: давайте уточним для забывших школьную математику, что такое линейная и нелинейная система отсчёта. Вот простая линейка:

Здесь каждое деление равно другому. И в начале линейки, и в середине, и в конце расстояние между рисочками одинаково, т.е. линейно.

А вот необычная линейка, логарифмическая, например:

Обратите внимание на верхнюю и нижнюю разлиновку шкалы. Она странная, очень неравномерная.

- И зачем нам такая «кривая» линейка по жизни? - спросите вы.

Незачем. Просто пример нелинейности, что такое нелинейная шкала. Измерять что-либо линейкой с такой шкалой вы ничего не будете.

А по поводу логарифма необходимо небольшое уточнение, т.к. нелинейных функций, зависимостей много, а логарифм/экспонента - одни. Это такие функции, которые показывают изменение не НА, а ВО сколько изменилась та или иная величина.

Например, мы можем сравнить два отрезка (две доски, если хотите) по длине и, в одном случае, первая доска окажется длиннее второй на 20 см, а во втором случае, длиннее в два раза. Хотя это одни и те же доски.

Привыкшие всё вокруг измерять «на», мы не обращаем внимания, что мы живём в мире «в».

Прим. Забавно, что такие (логарифмические, экспоненциальные) величины не могут быть отрицательными.

Самое распространённое и понятное – это звук. Громкость звука измеряется в дБ (децибелах) .

Это безразмерная величина. Есть некоторая «исходная», «эталонная» громкость (как эталон длинны метр, лежащий где-то в музее в Париже). И относительно этой величины измеряют какую-либо другую громкость, во сколько раз она больше ли меньше «эталонной».

Таким образом, мы можем слышать, прослушивать широкий по громкости диапазон звуков. От шороха в глухом тихом лесу, до рёва истребителя, болгарки или рок-концерта металлистов.

Изменяя дистанционкой громкость телевизора, вы изменяете уровень громкости во сколько-то раз.

Но со звуком ещё не всё. У звука есть, кроме громкости, второй параметр – это частота. Басы, средние частоты, высокие частоты. Частота звука также изменяется и воспринимается нелинейно, а в разах.

Все помнят раскладку чёрно-белых клавиш фортепиано или аккордеона. Частотный ряд там делится на т.н. октавы, которая в свою очередь делится на 12 нот. Ноты (частота звука) одной октавы отличаются от другой в 2 раза. Например, 440Гц, 880Гц, 1760Гц… и т.д. Это ноты «до» первой, второй и т.д. октав.

Со звуком разобрались. Ещё у нас есть свет. Установлено, что человеческий глаз способен реагировать, фиксировать «силу света» в несколько фотонов (понятно, что после того как глаз привыкнет к темноте). И в то же время мы можем взглянуть на Солнце. Но очень быстро и потом долго ждать, когда избавимся от «зайчика» в глазу. Это гигантский диапазон. Но, к сожалению, он не «логарифмирован», там шакала измерения силы света линейна.

Но в своих смартфонах, регулируя яркость экрана, вы можете наблюдать этот нелинейный эффект изменения яркости. Правда, он не очень ярко выражен, т.к. в самом смартфоне шкала уже нелинейна, да и датчик освещённости вносит свои поправки. Зато вы можете читать при свече или Луне, но зайдя с дневного света в тёмный подвал, где стоит та же самая одна свеча, никакой книжки вы не разглядите в первое время. Но зато пронаблюдаете эффект «В», вместо «НА». Убедитесь, что это явление «логарифмическо-экспотенциальное».

Кстати, на счёт второй характеристики света – цветности, т.е. частоты излучения. Да, у нас зрение имеет очень узкий спектр и поэтому в принципе мы можем обойтись линейной шкалой, измеряя длину волны в мм. Но сам спектр имеет явно выраженную нелинейность и работать со спектром удобнее в логарифмической шкале. Кстати, то же относится и радиоприёмникам, где есть длинные волны, средние, короткие, ультракоротки. И частоты радиостанций отстоят друг от друга не НА столько-то кГц, а ВО столько-то раз. И расчёт частотных фильтров так же иллюстрируется на логарифмической шкале.

Что у нас там ещё есть из чувств? Ну, тактильные ощущения. И снова тут логарифмическая зависимость. Вы можете ощутить прикосновение нежного пера, а можете сжимать черенок лопаты, копая картошку или рубить дрова – сумасшедший диапазон нагрузок, который так же удобнее измерять в логарифмах, в соотношениях, как звук.

Так вот, насчёт температуры… Что-то длинновато получилось. Давайте про температуру во второй части? А про производные чувств – в третьей.

Расшифровка мутного поста Притяжение, гравитация. Парадокс

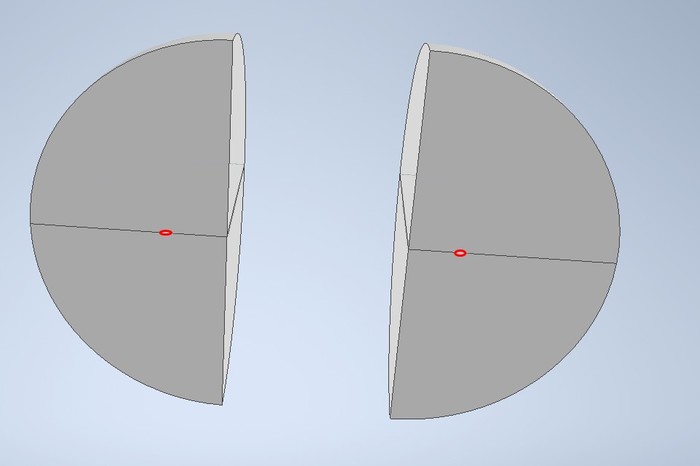
Рассуждения следующие. Берём шар. Пилим пополам.

Что там у нас в сечении?

Какие-то такие четвертинки. Ну, чтобы чисто посмотреть как там внутри.

Срез прямо таки является полукругом. Поищем, где у него центр тяжести. Находим такую картинку:

Резонно предполагаем (или не резонно?), что центр тяжести, а значит и центр масс, у полусферы будет находится примерно там же, возможно, чуть ближе к краю. Уже пометили красными точками.

Теперь мысленный эксперимент. Берём "пробное тело" (любой предмет) и располагаем его на поверхности шара. Целого шара. Все эти срезы/разрезы для удобства.

Значит он будет притягиваться к центру шара (Земли). Давайте распилим этот шар-Землю пополам. Как мы уже выяснили, центр тяжести, центр масс полшара будет находится где-то в обозначенных красными точками местах.

Значит, вектора притяжения пробного тела к этим центрам масс полусфер будут какими-то такими:

Вот эти вектора притяжения (сила притяжения) к центрам масс полусфер должны быть равны половине веса пробного тела? Ведь масса полусфер равна половине массы Земли при неизменном расстоянии.

Но в тоже время...

...при сведении полусфер, результирующий вектор получается меньше скалярной суммы векторов для полусфер.

Т.е. при неизменном расстоянии до центра масс полусфер, вес пробного тела уменьшается при сведении этих полусфер.

Какая-то ерунда, не так ли?