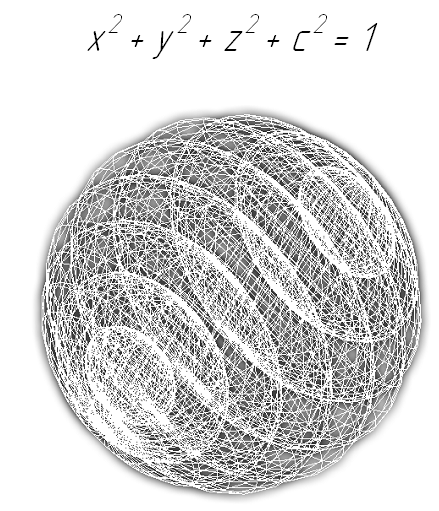Начну разбирать с объяснения всех пространств, до 8-мерного, а после уже разберу фигуры. Немного глоссария: Червячок- одномерное существо, флатландец- двумерное, гиперман с указанием цифры от 4 до 8- существо 4/8 мерное соответственно. Я исхожу из предположения, что зрение n-мерного существа будет n-1, по аналогии с человеком. Пластилином- значит в нашем мире, не на плоскости монитора.
О изображении 4 измерений.
Сначала просто попробую изобразить проекцию 4-измерений не на плоскости, а из пластилиновых линий. Плохое качество, но думаю вы поймёте мою мысль. Почему я выстроил именно так, а не иначе? Потому что проекцию 3 измерений на 2 некий обитатель двумерного мира вряд-ли увидит правильно. Тут и так же, просто смотря, при равной длине одномерных линий мы не увидим проекцию 4-измерений. Но как "флатландец" на свой одномерный "смартфон" сможет изобразить два измерения? Сложный вопрос. А одномерный "червячок" как изобразит на точку одно измерение? На эти вопросы ответа у меня нет, я не флатландец и не червячок. Наш гиперман-4 будет видеть просто полный объем т.е весь шар/сферу, весь куб.
5 измерений. Тут уже сложнее. Куда вытянуть 5 измерение? Проекцию можно сделать только в четырех измерениях, а в трёх- возвращаемся к червяку и пытаемся на точке изобразить три измерения. Невозможно изобразить, невозможно представить и невозможно понять даже проекцию. Вероятно будет являться вариантами объекта, т.е шестимерное существо (гиперман-6) будет в своих 5 зрительных измерениях видеть варианты объекта. А гиперман-5 будет видеть объект на всем протяжении его существования.
6 измерений. Проекция только на пяти, пытаться изобразить 6 даже "пластилином" будет как попытка точки изобразить три измерения на... ничём, на -1 измерении. Про минусовые измерения можно написать на пару страниц 11 шрифтом, но я не буду. Вероятно, гиперман-7 видя своим 6 мерным зрением будет видеть все варианты объекта за всю историю его существования.
7 измерений. Говорить ничего не буду, понять его и что в нём могло бы быть- задача непосильная. Вероятно, варианты тех вариантов что были представлены в 5 измерении. Иного не вижу. Хотя с объяснением пошла рекурсия, что, мягко говоря, не любят математики.
8 измерений. Тут уже заканчивается даже логика и начинается нечто, что способны понять немногие. Вероятно, 8 измерений будет как вся история всех вариантов всех вариантов объекта. По такой же рекурсивной схеме можно построить любое измерение, но это скучно. А так да, мы просто трехмерные людишки и мы не можем понять.
Начну с четырёх. Тут будет гиперкуб, Тор Клиффорда и 3-сфера. Заметили, почему сфера лишь три измерения? Потому что 2-сфера огибает 3-шар, следовательно 3-сфера должна огибать 4-шар. Вот пара картинок, пытающихся изобразить трехмерную сферу.
Теперь Тор Клиффорда. Тор Клиффорда «плоский». Он может быть выровнен в плоскость без растяжений, в отличие от стандартного тора вращения. Тут картинка не даст понять всё, внутренность проекции тора эквивалентна его внешности, что непросто понять визуально. Почему его внутренность эквивалентна его внешности- он делит 3-сферу на две части. Даже не спрашивайте почему, пожалуйста.
Ну и Тессеракт. Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
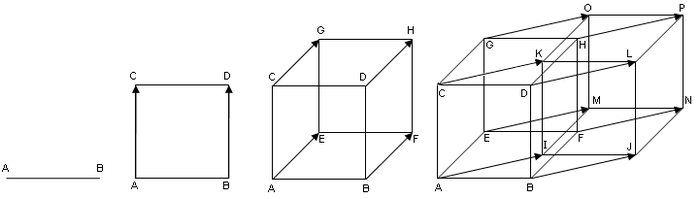
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAEGHF. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.
Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAEGHF, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.
Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAEGHF и KLJIMOPN, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.
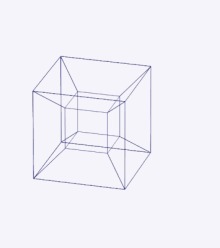
Вот вам просто тессеракт:
Вот вам его развёртка, статичная и анимированная:
Вот вам его вращение. Преломление граней из-за того, что это будет как вращение одномерной проекции трёхмерного куба, т.е очень неполноценно изображено.
Брать пятимерный куб сложно, не так просто его изобразить, невозможно даже с преломлением граней изобразить его вращение да и он сам сложный.
Да, гифка с вращением баян. Но одна картинка не влияет, текст мой, изображения с интернета.