Я уже рассказывал, что математика — очень красива. Но многие не видят этого из-за строгого и сухого языка, на котором она говорит. Сегодня я постараюсь объяснить, почему царица наук такая строгая, в чём смысл такого языка и его преимущества
В математике нет лишних слов
Возьмите любое математическое определение. Да, скорее всего оно будет написано языком суше песков Сахары. Но ни одно слово не попало в это определение зря. Всё, что не было необходимо для передачи мысли, было безжалостно отброшено
Если вы не любите пустых слов, математика — дисциплина для вас
Слова строго определены
Да, порой математические термины звучат очень страшно. Но каждый из них строго определён. Если вам встретилось непонятное слово в определении, всегда можно посмотреть значение этого слова. Если и в нём будут непонятные термины, можно прочитать и их и так пока не уткнёшься во что-то ещё не описанное. Тогда нужно всего лишь изучить свойства этого объекта. У меня так брат Филдсовскую премию получил
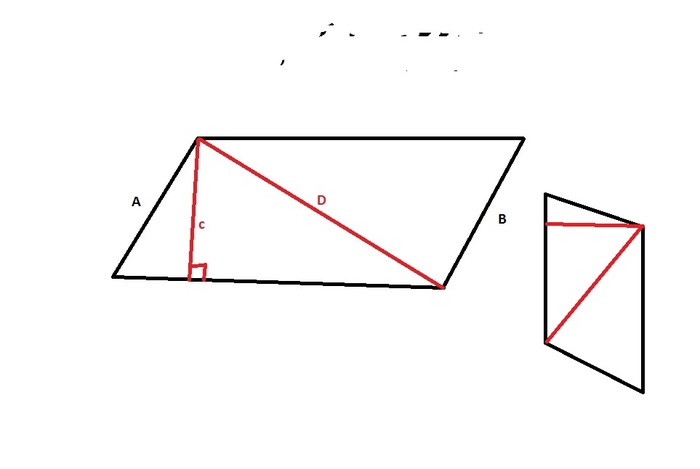
Преимущества такой строгости видно на обратном примере. Вы могли слышать про парадокс кучи. Представьте, что перед вами куча песка:
Кто-то очень терпеливый начинает убирать с неё по одной песчинке. Вот песчинок уже не несколько тысяч, а всего одна, теперь сотня… Так с какого же количества песчинок куча перестаёт быть кучей? А если наоборот, на пустое место добавлять по одной крупинке песка, когда образуется куча?
Это не математический, а чисто лингвистический парадокс. Вся его проблема в том, что слово куча строго не определено. Точно скажите, что же это такое и математика позволит описать все её свойства
Математика безгранична
Естественные науки не могут изобретать какие угодно теории: они ограничены реальным миром. Математике же это не очень интересно: если её законы можно приложить к реальному миру, это лишь удача для реального мира. Но зачем математику ограничиваться 3-мерным пространством? Его интересуют более общие случаи. Четырёх-, пяти-, n-мерное пространство! Бесконечности, абстрактные структуры, не существующие в реальном мире, всё это описывается математически!
«Как мило, у него воображаемый друг!» — игра слов с мнимой единицей — корнем из -1
Вся математика — на кончике карандаша
Вам не нужно дорогое оборудование для того, чтобы заниматься этой наукой. Всё, что нужно для того, чтобы открыть что-то новое в математике — это бумага и карандаш. Вы можете открывать новые объекты сами, придумывая их свойства, или взять ряд известных правил и попытаться описать новые свойства объектов в них
Это аксиомы Евклида. Большая часть учебников, которые были у вас в школе, выводится из этих простых правил, вмещающихся на одной странице!
Да, понять математику бывает сложно. Порой сложно определить, насколько сложным является то, что скрывается за терминами
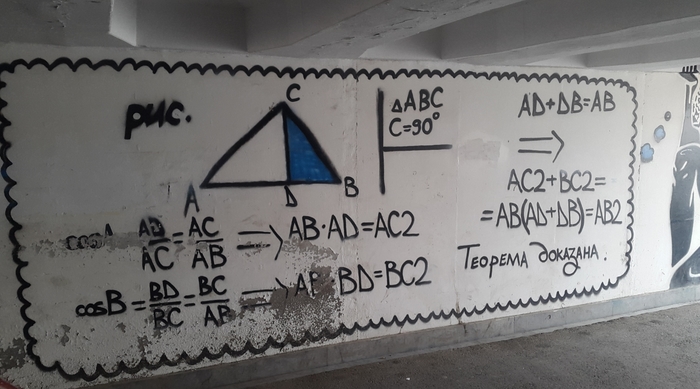
Вот вам тест. Две теоремы ниже являются школьными, а за доказательство третьей была предложена награда в 1 миллион долларов. Сможете ли вы угадать за какую?
Столбцы матрицы , входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы линейно выражается через остальные столбцы из базисного минора
Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере
Из всякой ограниченной последовательности точек пространства можно выделить сходящуюся подпоследовательность
Пишите свои предположения в комментариях :) А если интересны посты о науке и учёбе, заглядывайте в мою группу ВК