Здравствуйте дорогие пикабушники.
Заранее предупреждаю, никакого отношения к текущим событиям в сфере политики не имею,аккаунт не консерва,а старый благополучно забытый акк с неизвестно какой целью ранее созданный. Просто за многие годы я так и не решался чего нибудь запостить или даже просто комментировать.
А теперь к сути дела. Я к сожалению не знаю у кого тут такие вопросы спрашивать поэтому просто пилю пост. Также прошу не сильно пинать,увы,у меня диагноз синдром Аспергера (F84.5),а поэтому я бываю буквальным,могу не понимать каких то правил,ну и здешние процедуры мне малознакомы.
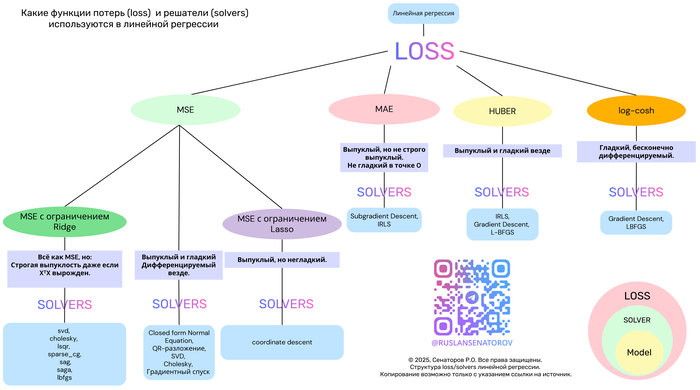
Я занимаюсь исследованиями в области машинного обучения,обработки естественного языка и вопросами машинного сознания,на текущий момент тружусь над вопросами разработки мультимодальных нейронных сетей с динамически изменяемой структурой. Это в действительности любимая работа для меня (например мало с чем можно сравнить радость от того как ты в действительности видишь прогресс,то как ты видишь что твоя система обучается как надо). Но у меня есть одна заковыка во всем этом. Я работаю над исследованиями самостоятельно,и разумеется все это я делаю за свой счет (главным образом оборудование,ну а что видеокарты нынче стоят как почка все и так знают) - это первое. Во вторых,в моем текущем окружении я крайне часто встречаюсь с саботажем моих усилий (моим нынешним преподавателям всегда было крайне неприятно когда студент и сам может завалить горе-педагога на его же экзаменах,но конечно же,не все таковы),встречаюсь с нежеланием университетского руководства что либо делать с печальной ситуацией в организации (статьи им подавай,а вот как ты это будешь делать уже никого не колышет,а я хреновые или сырые работы из принципа не публикую). Я тем не менее все равно продолжаю клеить свои системы,писать научные статьи о новых придуманных мной архитектурах потихоньку в одиночку. И отсюда проистекает важное но:
я работая в этой области (я на текущий момент студент,исследователь и преподаватель в одном лице), делая публикации много раз натыкался на недобросовестное рецензирование статей (был случай когда во вшивый журнал из РИНЦ меня рецензент отправил в пешее эротическое придравшись к словам о значении которых он не догадывался,но зато на австралийской конференции англоязычный вариант приняли со свистом) я понимаю что в России на пути может оказаться чрезвычайно много препон а поэтому я подыскиваю возможности выезда из России куда нибудь еще дабы попробовать себя и там. Я решил на шару написать пока пост сюда,ибо много раз был свидетелем многогранности сообщества пикабу. И так вопрос - есть ли здесь кто нибудь из моей области исследований (машинное обучение,искусственный интеллект,машинное сознание,вычислительная математика,матанализ)? Если есть(хотя любой совет может оказаться неожиданно полезным,так что слушаю любых людей из академической среды РФ) то такой вам вопрос - что вы можете посоветовать мне потенциально сделать в моей ситуации (ситуация следующая: Временно заперт в своем университете, из-за нехорошей славы университета публикации часто не удается сделать,очень много людей которые очень хотят ни черта не делать и выйти в соавторы,преподаю математику,мат логику и основы практического машинного обучения в своем же университете и в местной шараге. Ситуация кажется мне нехорошей из-за того что на финансирование исследований и качество работ заливается болт + ко всему среди персонала университета часто встречаются люди с совершенно нездоровой тягой к впихиванию в статьи прикладной части которая выглядит по идиотски(ей богу,порой даже на peer-review отправить стыдно),несмотря на то что все исследование исполнялось как фундаментальное и о немедленном приложении речи не шло. Ну вот по этому поводу и хочу узнать у вас,дамы и господа. Куда можете посоветовать податься в нашей стране или за рубежом (не важно,важно чтобы работать было можно как следует)? Если что - я уже заканчивающий бакалавр 4 курс (специальность - прикладная информатика),магистратуры нет, есть только публикации,все необходимое для работы с продвинутыми интеллектуальными системами я изучил сам (слава libgen'у и сайтам для добычи полных версий научных статей). Идея об отъезде за рубеж родилась из моего общения с моей коллегой и подругой из Питтсбурга.
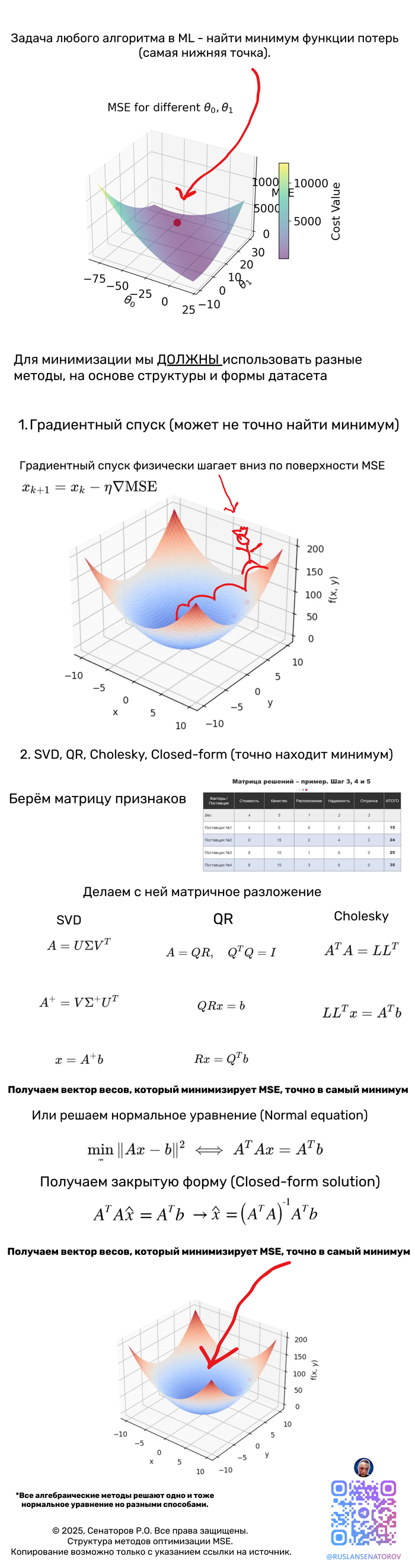
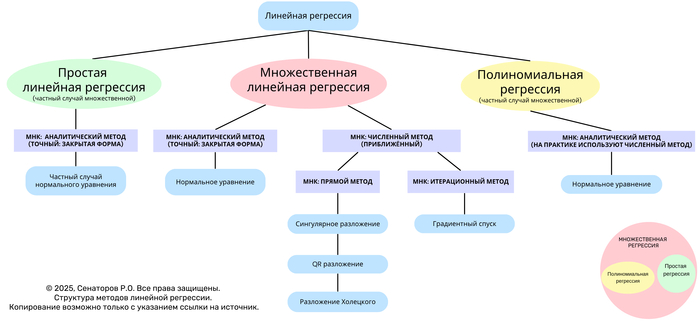
Также сразу же хочу спросить любых людей читающих сей пост - не будет ли вам интересно если бы я начал публиковать собственные посты о состоянии машинного обучения с простыми (по возможности) объяснениями,применимости этих технологий и всякое такое,у меня скопилась большая выборка хороших,годных материалов собственного написания по этой теме (в конце концов,я преподаю,а такие дисциплины с полоборота закатать студентам сложно без хорошего предварительного объяснения)?
Извиняюсь за возможно странные формулировки - пожалуйста пните меня и уточните что я имел ввиду. Сразу заранее извиняюсь за возможно допущенные грамматические ошибки,просто за последние годы английский язык стал для меня роднее русского.
Спасибо всем за внимание.
Всем мира,любви и счастья, дорогие друзья.