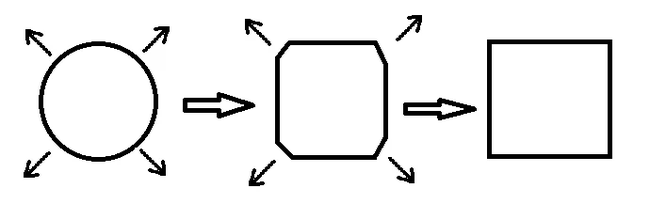
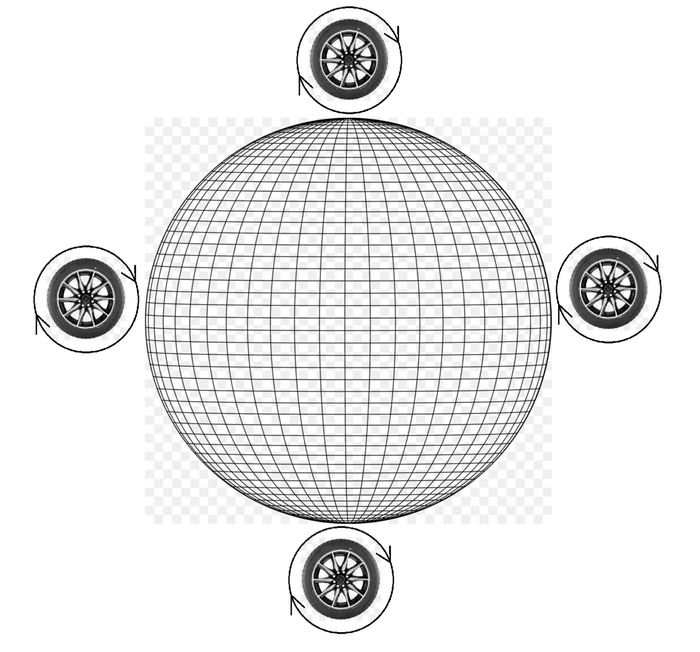
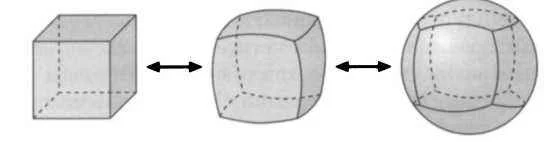
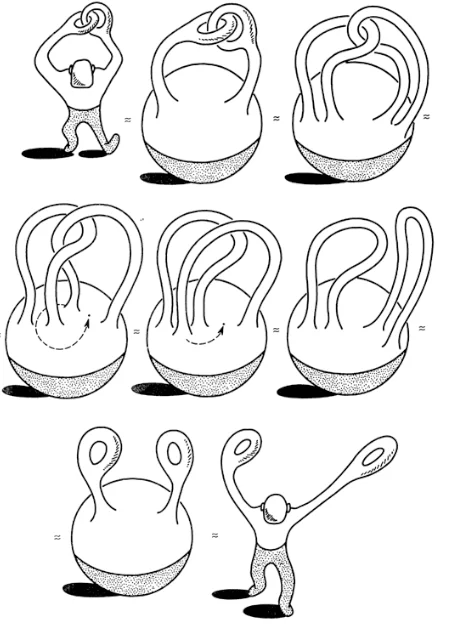
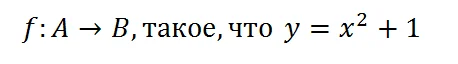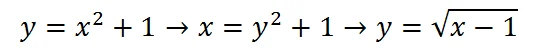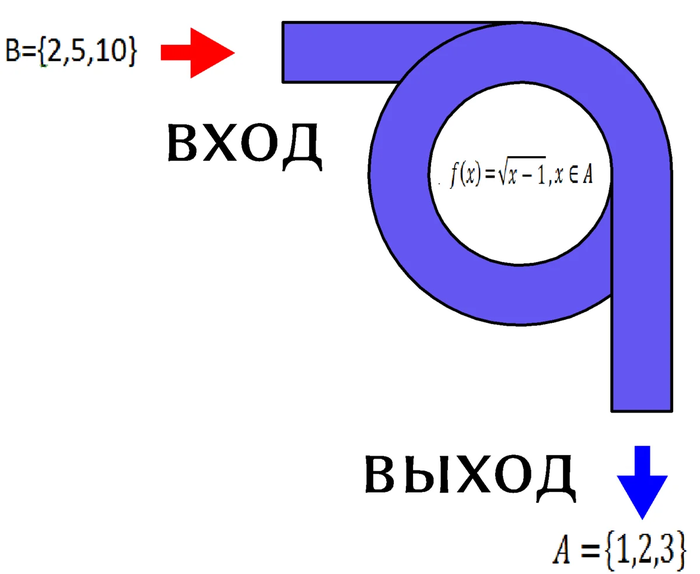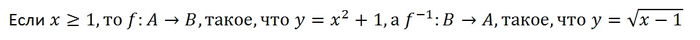Отображение множеств для начинающих. Введение в теорию множеств
Перед Вами один из самых интересных уроков из теории множеств, и в то же время очень важный. Разобравшись с отображениями, мы вплотную подберемся к гомеоморфным преобразованиям. Итак начнем!
Что такое отображение?
На самом деле каждый школьник, начиная с 6-7 класса, когда вводится понятие "функция", постоянно сталкивается с отображениями.
Определение. Функция - это соответствие между элементами двух множеств , установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества. Другими словами, функция взаимно однозначно отображает элементы одного множества в элементы другого. Вот наглядный пример:
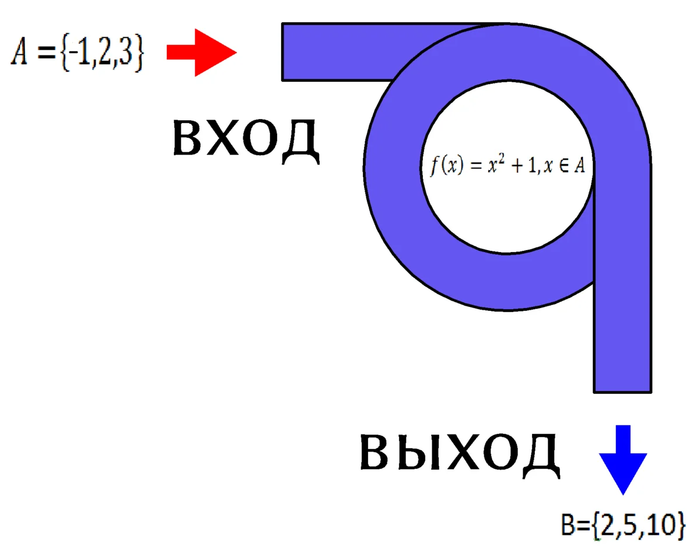
На вход подаются элементы множества А (которые обозначим x), по пути в петле они определенным образом преобразуются: т.е. каждый элемент возводится в квадрат и складывается с единицей. На выходе получаем множество B уже с новыми элементами y. Обратите внимание, что каждому элементу множества А соответствует один элемент множества B.
В данном случае мы записали такое отображение множества А в множество B, что любому x, принадлежащего А поставлен в соответствие один элемент y, принадлежащий B, который вычисляется по указанному правилу.
Элементы x множества A - называются прообразами, элементы множества B - образами. Не правда ли, элементарно!Всё прекрасно, разобрались, а давайте теперь на верхнем рисунке поменяем вход и выход местами и преобразуем вид функции f, чтобы из элементов множества B получить элементы множества А, иными словами, попробуем задать обратное преобразование.
Чтобы получить обратное преобразование, мы просто поменяли местами x и y.
Всё было бы хорошо, если бы не одно НО. На выходе у множества А первый элемент равен 1, в то время как изначально была -1.
Главное отличие вышеуказанных отображений следующее: если в первом случае образом может быть любое число, то во втором случае образом может быть только любое положительное число больше 1.
Данный факт заставляет задуматься, а какие виды отображений существуют и всегда ли есть отображения обратные данному?
Классификация отображений
Не буду лишний раз загружать Вас формулами, а поясню всё на трех рисунках.
1. Отображение называется сюръективным или сюръекцией, если каждому элементу первого множества соответствует хотя бы один элемент второго множества, т.е. каждый элемент второго множества имеет хотя бы один прообраз в первом множестве. Обратите внимание, употребляют предлог "на".
Пусть A - множество контрольных работ учеников 11а класса, тогда учитель математики, при проверке делает не что иное как отображает их на множество оценок B={2,3,4,5}. Если работ, например, 15, то несколько их них будут написаны на 2, какие-то на 3 и так далее, что говорит о том,что учитель выполняет сюръекцию.
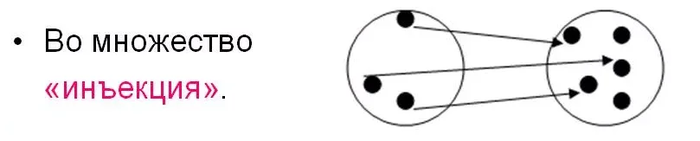
2. Отображение называется инъективным или инъекцией, если каждому элементу первого множества соответствует только один элемент второго множества, т.е. каждый элемент первого множества является прообразом только одного элемента второго множества. Обратите внимание, употребляют предлог "в".
Пусть А - множество шприцев с вакциной от коронавируса, а B - множество людей. Очевидно, что среди людей есть переболевшие люди с приобретенным иммунитетом, которым вакцина не нужна, а шприцев с вакциной меньше, чем всех людей вместе взятых. Так вот, врачи, выполняя вакцинацию с использованием всех шприцев, выполняют инъекцию (да, каламбур) множества шприцев в множество людей. В итоге не каждому досталось вакцины - это ключевое отличие инъекции, от сюръекции.
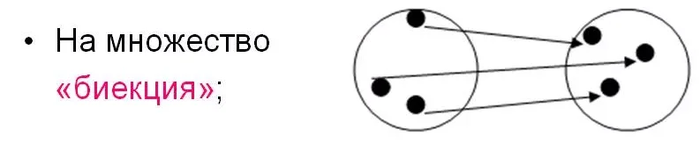
3. Отображение называется биективным или биекцией, если оно сюръективно и инъективно одновременно. В пояснении, думаю, не нуждается: каждому элементу А соответствует только один элемент B. Функция в классическом определении - есть биекция.
Теперь разрешим проблему, которая появилась после попыток вернуть множество B в множество A, записав обратную функцию. Во-первых, дело в том, что обратная функция существует только для биекций. Во-вторых, всё очень сильно зависит от исходных множеств. Например:
Указанные отображения называются взаимно-обратными (обратное обозначается с -1 в верхнем индексе). На другом множестве, например, при x>0, эти отображения не будут взаимно обратными, т.к если элемент x равен 0, то получить его указанным обратным преобразованием не получится.
Другие интересные материалы на моем ДЗЕН-канале "Математика не для всех" ( здесь - путеводитель по каналу).