Почему человек - это шар с ручками: изучаем математическую топологию. Часть1. Введение
Этой статьей начинаем с Вами изучение одного из самых сложных и запутанных, но одновременно прекрасных, выверенных, наглядных и точных направлений математики - общей топологии. Название - не игра слов, к концу этой заметки Вы поймете, как математика относится ко всему роду homo sapiens. Начинаем!
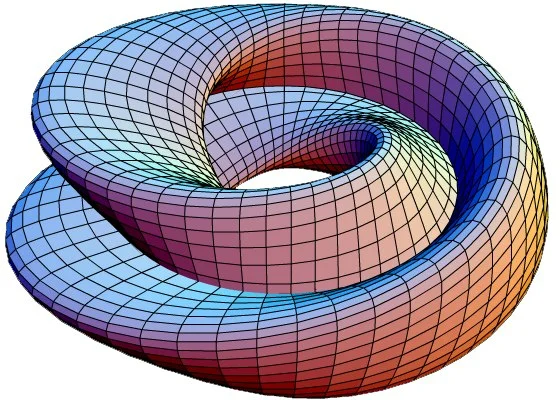
Не правда ли завораживает? Какими свойствами обладает это фигура, можно ли ее построить в нашем трехмерном мире, как пройти из одной точки в другую?
Тополо́гия (от др. греч τόπος — место и λόγος — слово, учение) - наука, изучающая качественные свойства фигур не только в привычном нам трехмерном мире, но и в мирах с большим и меньшим количеством измерений (уж поверьте все вы сталкивались с ними, только может быть не догадывались).
Самый простой пример пространства меньшей размерности - это плоскость у которой размерность равна 2, подобно тому, как у прямоугольника есть ширина и длина.
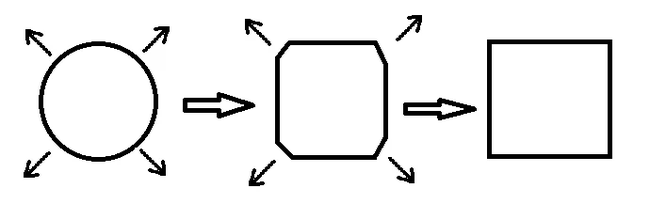
Проделаем такой эксперимент: возьмем на плоскости квадрат и начнем его сжимать по краям, как бы сглаживая углы. После некоторого количества движений и выравниваний мы сможем получить круг - другую геометрическую фигуру. Процесс обратим - из этого круга мы всё так же можем получить квадрат. Значит ли это, что квадрат равен кругу, а круг квадрату? Конечно нет, но обычный человек сказал бы: "Они подобны", а тополог скажет: "Они гомеоморфны или получены гомеоморфным преобразованием".
Стрелки - направление растягивания.
Страшное слово? Как бы не так! Каждый из Вас (во всяком случае женская половина моей аудитории)за свою жизнь проводил гомеоморфные преобразования: "отщипнул тесто - сделал из него шар - раскатал в блин".
Гомеоморфное преобразование - это ни что иное, как растягивание или сжатие точек какой-либо фигуры без образования разрывов и склеек одинаковых точек. Возьмите раскатанный блин и порвите его по центру - получите негомеоморфное преообразование.
Возникает резонный вопрос, а какие свойства остаются неизменными при гомеоморфизме? Математики называют такие свойства качественными или топологическими и если мы хотим говорить о них, то должны как-то охарактеризовать эти свойства, хотя бы интуитивно-наглядно. Очередной эксперимент:
Возьмем сферу - поверхность точек, равноудаленную от другой точки, называемой центром сферы. Сфера - пуста, если наполнить сферу любым веществом (в нашем случае мягким и эластичным) получится шар. Попытаемся понять, чем "топологически" отличается сфера от шара?
1) Зададимся вопросом: как наикратчайшим образом добраться из одной точки сферы в другую, противоположную ей (например. с северного на южный полюс)? Правильно, пойти как нормальный человек по поверхности. А для шара? Теоретически мы могли бы "срезать" добрую часть путь проникнув через его центр и прошив его насквозь. Есть отличие!
Напоминаю, что по "пустоте" мы не перемещаемся, а внутри сферы - пустота.
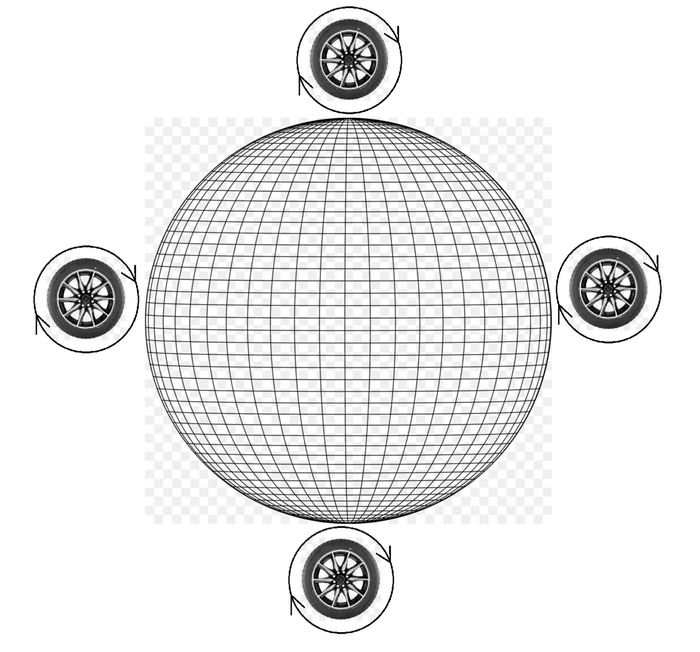
2) Представьте, что вы решили прокатить по поверхности сферы колесо и вернуться в ту же точку. Изменится ли направление его вращения после Вашего с ним кругосветного приключения? Очевидно и для сферы и для шара, что нет.
Именно поэтому у кругосветных путешественников-автомобилистов колеса по приезду в родной город не крутятся в другую сторону
Но есть фигуры, прокатив колесо по которым и вернувшись в ту же точку мы изменим направление его вращения! Пример - широко известный лист МёбиусаЭто свойство фигур называется ориентируемость. Шар и сфера - ориентируем, а вот лист Мёбиуса - нет. Здесь отличий между шаром и сферой не выявлено.
3) Из определения следует, что под поверхностью сферы пустота. В шаре такого нет, он заполнен полностью.
Именно в третьем различии вся "соль". Что же из него следует?
Представьте, что Вы взяли комок мокрого снега и хотите придать ему идеальную форму.
Снег еще рыхлый, поэтому сжимая снег со всех сторон Вы начнете "стягивать" точки этого шара к одной из его точек - центру.
А теперь попробуйте стянуть футбольный мяч хотя бы к одной его точке. Попробуем стянуть северный (N) и южный полюса (S). Суть в том, что в предельном приближении мяч порвется в точках W и E, а разрыв, как мы помним из определения, недопустим при гомеоморфизме.
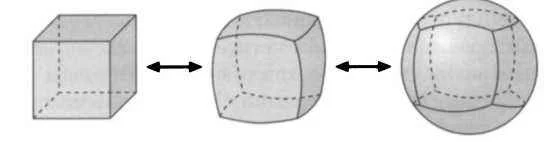
Таким образом, мы не смогли гомеоморфно стянуть сферу к какой-либо из своих точек (зато сферу мы можем вывернуть наизнанку - видео в конце статьи), а шар смогли. В этом и заключается топологическое различие между этими фигурами: шар не гомеоморфен сфере. Остается открытым вопрос: чему же тогда гомеоморфен шар и сфера? Ответ: кубу.
Со сферой всё намного интереснее. Топологи различают сферу без ручки (тогда это просто сфера) и сферу с n-ручками, где n=1,2... Например, сфера с ручкой получается с помощью гомеоморфных преобразований из тора (бублика).

Что же общего у кружки и тора? Ответ: количество дырок, и это ключевое топологическое свойство фигур. Фигуры с разным количеством дырок не могу быть гомеоморфны другу другу, не могут быть получены друг из друга посредством сжатия/растягивания. И это главный вывод нашего вводного экскурса.
Стой, стой, а что же с человеком, который - шар с ручками?
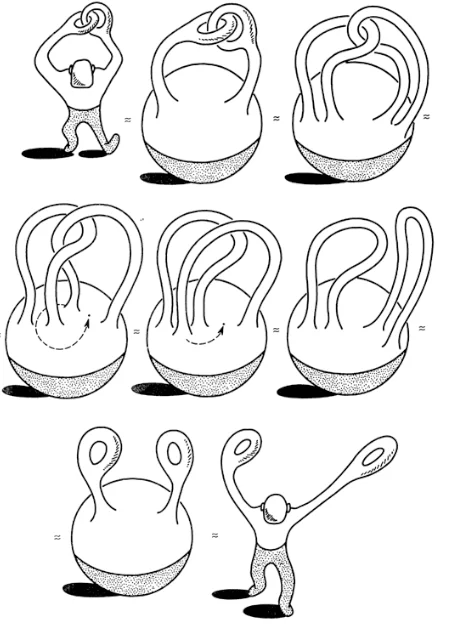
Ах да, знакомьтесь - это человек-Шар и он попал в передрягу: у него руки закреплены между собой как два кольца. Ему нужно помочь распутать руки не разрывая пальцы. Вы скажете невозможно, топологи скажут: элементарно.
Спасибо за прочтение! Материал написан лично мною и взят с канала "Математика не для всех", который да-да-да базируется на платформе Дзен. Сейчас уже вышли три материала по теории множеств ( вот 1, 2 и 3), необходимые для введения в топологию.
Оказывается, там не только чернуха и трэш, но и вполне себе интеллектуальный контент бывает. Буду рад комментариям и подпискам. На данный момент на канал подписано около 300 человек.