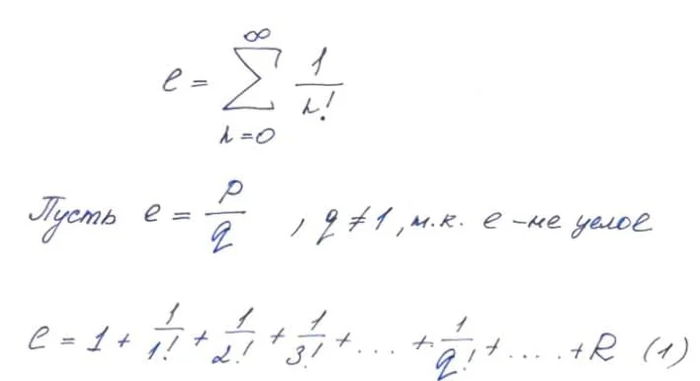MathNotForYou

UPD. К посту есть вопросы #comment_198298406

"Математика не для всех" снова на связи, приветствую Вас, уважаемые Читатели! Сегодня хочу рассказать Вам об одном удивительном факте, который узнал совсем недавно. Оказывается, покупая пазлы на 2000 элементов, Вы можете быть практически уверены, что Вас "обманули" на целых 2 кусочка! Давайте вместе разберемся, почему и при чём здесь математика. Поехали!

Кстати, если у Вас есть пазлы на 500 элементов, то будьте уверены, что и на самом деле их будет столько же. А вот с двумя тысячами...

Ситуация такая: все отдельные пазлы, хоть и имеют разную форму, но вырезаются из прямоугольника. При изготовлении пазла необходимо найти два целых числа, которые будут при умножении давать 2000. Учитывая разложение числа 2000 на простые множители, получаем такие варианты:

Из более-менее подходящих только два последних варианта. Чем же они плохи? Дело в том, что производители стремятся к соотношению сторон пазла как у стандартного листа А4, которое примерно равно 1,4. В нашем же случае получается:

В таком случае изображение получилось бы либо слишком вытянутым либо слишком квадратным. Решение есть! Используем число 1998, которое замечательно раскладывается на множители:

Это уже намного приятнее для глаза и удобнее для подбора картинки. Вот так обычные числа определяют дизайн предметов, которые нас окружают. P.S. Проверим количество?

Больше интересной математики в телеграмм - "Математика не для всех"

Приветствую Вас, уважаемые Читатели! "Флатландия: роман о четвертом измерении" (1884) - одна из важнейших книг, которая распространила идеи о пространствах высших измерений в широких кругах общества.

Английский теолог и школьный директор Эдвин Эбботт Эбботт (1838 - 1926)

Действие книги происходит в двухмерном мире, а главным персонажем является мистер Квадрат, который через череду занимательных рассуждений подводит читателя к мысли, что и сами люди не могут быть до конца уверены, что их трехмерный мир единственный.

Кроме всего прочего, роман является хлесткой социальной сатирой, затрагивающей вопросы равенства. Предлагаю узнать подробнее об этом замечательном произведении. Поехали!

ЧАСТЬ I

В первой части книги автор описывает удивительный мир, в котором происходят действия новеллы. Этот мир является плоским, а живут в нём прямые линии, треугольники, квадраты и т.д., вплоть до окружностей. Интересно, что геометрические различия напрямую связаны с положением в обществе:

Самые бесправные существа - женщины. У них нет углов, образования и вообще никаких прав. Мужчины оправдываются, что это лишь потому, что конфигурация тел женщин природно несовершенна.

Равнобедренные треугольники - это солдаты и рабочие, а средний класс имеет форму треугольников равносторонних. Все, кто имеют хоть какую-то профессию, содержат четыре и больше углов. Чем больше углов у фигуры, тем к более благородному сословию она относится.

В домах флатландцев пять углов и отдельные входы для женщин и мужчин. Крыши домов всегда направлены на север. т.к. дождь всегда идет согласно силе гравитации - с севера на юг.

Наконец, когда углов становится столько, что фигуру уже не отличить от окружности, она становится окружностью - жрецом плоского мира Флатландии.

Как можно заметить, все фигуры, начиная со среднего класса, - правильные. Неправильность фигуры - показатель нечистоплотности и маргинальности, поэтому за ними постоянно наблюдают, а после наступления совершеннолетия подвергают освидетельствованию. По его результатам фигуру могут сослать на самые неблагодарные работы или даже уничтожить.

Жители Флатландии узнают друг друга либо на ощупь, как низшие слои, либо как средний класс, квадраты и пятиугольники - по голосу. Высшие слои ориентируются по "расплывчатости" сторон в условиях постоянного тумана, царящего в стране. Например, для небольших углов равнобедренных треугольников стороны расплываются почти сразу, а для больших углов 17-угольника это происходит медленнее.

Социального лифта во Флатландии нет. Единственная возможность - это дети. У детей мужского пола обычно на один угол больше, чем у родителей, а у неправильных фигур иногда рождаются правильные, которых потом усыновляют более "важные" фигуры.

На вершине социальной лестницы находятся жрецы, которые занимают ведущие посты в управлении государством и во всех сферах жизни общества. Они ничего не делают, а лишь побуждают другие фигуры, беспокоятся о Флатландии, не щадя живота своего.

ЧАСТЬ II

Во второй части мистеру Квадрату - ученому, пытающемуся познать окружающий мир, придется отправиться в Лайнландию - одномерную страну, в которой есть только прямые (мужчины) и точки (женщины). Квадрат безуспешно пытается разъяснить королю линейного мира, что, "если отрезок в его мире начнет перемещаться вверх, то получится квадрат".

После этого герой отправится в Спейсландию - мир с тремя измерениями, который содержит в себе Флатландию. В этом мире правит Сфера, которая уже мистеру Квадрату попытается объяснить, что если квадрат переместить вверх, то получится куб. Оставив все попытки, Сфера решит пересечь Флатландию сверху вниз, но мистер Квадрат видит лишь только сечения разной величины и решает, что это лишь происки жрецов:

Убедившись в тщетности своих намерений, Сфера выносит Квадрата за пределы Флатландии, после чего всё встает на свои места, и главный герой понимает концепцию трехмерного мира. Мистер Квадрат чувствует, что можно пойти и дальше, после чего заявляет Сфере, что и она, вероятно, всего лишь проекция из четырехмерного мира. Заканчивается роман тем, что мистера Квадрата сажают в тюрьму за попытки описать мир с тремя измерениями.

P.S.

"Флатландия: роман о четвертом измерении" предлагает в образе плоского существа исследовать свой мир, чтобы потом логично прийти к идее миров меньшей и большей размерности. Новелла позволяет читателям сполна ощутить всю сложность представления иных миров и, заодно, задуматься о мироустройстве нашей Вселенной. Читать обязательно!

Больше интересной математики в телеграмм - "Математика не для всех"

Приветствую Вас, уважаемые Читатели! Сегодня такой легкий материал, прошу его не воспринимать излишне серьезно. Естественно, дважды два равно четыре и "это всем известно в целом мире". С другой стороны, а что значит известно всем? Это аксиома? Догма? Оказывается, что нет: это всего лишь математическое суждение, которое требует доказательства. Оно простое, но в то же время фундаментальное. Поехали!

Как говорят о натуральных числах в школе?

Их определяют либо словесно "Один, два, три, четыре", либо с помощью арифметической прогрессии, которая начинается с 1 и имеет разность 1, либо как множество строк цифр, которые не начинаются с нуля и т.д.

Примерно так и размышляли математики (на самом деле особо не заморачивались) до выхода на сцену Джузеппе Пеано. Он первым ввёл простую аксиоматику, позволившую формализовать арифметику:

1. Существует 1 (единица) - единственное натуральное число, которое не следует ни за каким другим.

2. Для каждого натурального числа а существует следующее за ним (определяется т.н. "функция следования S(x)") число а' при том единственное. Это, во-первых, значит, что число натуральных чисел бесконечно, а второе - что между последовательными натуральными числами нет каких-то других.

3. Аксиома индукции: если какое-либо предположение доказано для 1, и если из допущения, что оно верно для n следует, что оно верно для n+1, то предположение верно для всех натуральных чисел.

В аксиоматике Пеано определены свойства сложения и умножения:

(а + b)' = a + b' (например, (2 + 3)' = 2 + 3' = 2+4 = 6).
a' = a + 1 (например, 3' = 3 + 1 = 4).
a x b' = (a x b) + a (например, 3 х 4' = 3 х 4 + 3 = 15).
a x 1 = a.

Вооружившись знаниями аксиом и правил умножения/сложения можно перейти к доказательству. Прежде всего надо понять, что такое 2 и что такое 4. Вспоминаем про функцию следования. Очевидно, что:

S(1) = 2, тогда S(2) = 3, S(3) = 4 или
2 = 1' и 4 = 1'''

Теперь докажем, что дважды два - это два плюс два. Итак, 2 = 1', тогда:

1' x 1' = (1' x 1) + 1' (свойство 3)
1' x 1 = 1' (свойство 4), значит 1' x 1' = 1' + 1'

Осталось теперь доказать, что 2 + 2 равняется четырем:

1' + 1' = (1' + 1 ) ' (свойство 1 в обратную сторону)
1' + 1 = (1')' = 1'' (свойство 2), значит 1' + 1' = (1'')' = 1''' = 4

Вот, собственно, и всё доказательство. Можете быть уверены, что, во всяком случае, на множестве натуральных чисел дважды два равно четырем. Спасибо за внимание!

Больше интересной математики в телеграмм - "Математика не для всех"

Постоянному читателю моего канала конечно известно, что такое рациональные числа. Напомню, что это числа вида m/n, где m - натуральное, а n - целое число. Однако уже в древней Греции было известно, что есть и числа, которые нельзя представить в виде такой дроби.
Греки назвали их иррациональными, однако долгое время не удавалось построить их точную аксиоматику, определить эти самые "неразумные" (иррациональные) числа через арифметику "разумных". Сделать это окончательно удалось лишь в 1858 году немецкому математику Рихарду Дедекинду в статье "Непрерывность и иррациональные числа". Причем вышло у него всё настолько тривиально и одновременно красиво, что грех этим не поделиться. Поехали!

Сам Дедекинд был очарован идеей выразить иррациональные числа как следствие "простейшего арифметического акта - счёта, который представляет собой последовательное представление бесконечного ряда положительных целых чисел, каждое из которых определяется числом, ему предшествующим". Со сложением и умножением таких чисел проблем не было : каждый результат этих операций являл собой число из этого ряда.

Возьмем все натуральные числа. Сложив 5 и 7 мы получим число 12 из того же класса. Умножим 5 на 7 получим 35 - число тоже натуральное.

Однако с вычитанием и делением ситуация проблема. Определив вычитание (например, 5 - 7 = -2 - число из другой "вселенной", относительно натуральных) , мы дополнили натуральные числа отрицательными, выделив класс целых чисел. Операция деления (5/7 - на пальцах не посчитать) заставила ввести и рациональные числа. Выбросив из них 0, математики "замкнули круг", определив поле рациональных чисел R, замкнутое относительно четырех арифметических операций.

Что мы знаем об этом поле? В нём существуют понятные каждому законы:

1. Если число a > b, b > c, то a > c. На числовой прямой, иначе говоря, это будет значить, что b лежит между a и c.
2. Если a и b различные числа, то между ними существует бесконечное количество других чисел.

Без потери общности можно рассматривать только положительные рациональные числа
3.

Если a - есть рациональное число, то все числа в R распадаются на два класса: те, которые на числовой прямой лежат слева от а (класс А1) и те, которые лежат справа от a (класс А2). Для каждого числа из класса А1 известно, что оно меньше числа из класса А2:

Важно добавить, что число a является наибольшим элементом в A1 либо в наименьшим в A2.

Само число а можно произвольно отнести к первому или второму классу, но самый важный вывод в том, что получено определение рационального числа а как сечения (A1, A2). С другой стороны понятно, что каждое заданное таким образом сечение определяет натуральное число.

Но есть ли сечения, которые не могут быть проведены рациональными числами? Конечно, и их бесконечное количество. Самый простой пример - это √2, совершивший революцию в восприятии числовой прямой, ставший удивительным подтверждением её непрерывности и подтвердивший, что между рациональными числами есть пробелы.

На самом деле, сечение, производимое √2 имеет значительные различия от сечений, которые производят рациональные числа. Например, в классе А1 (красный цвет) нет наибольшего числа: мы сколько угодно можем приближать к √2 слева, применяя всё более точные рациональные дроби, но никогда не найдем "того самого наибольшего". Такая же ситуация и справа: для класса А2 (синий цвет) никогда не найти "наименьшего" в мире рациональных чисел.

Тогда Дедекинд постановил: всегда, когда мы будем встречаться с сечением такого вида, у левого класса которого нет наибольшего, а у правого - наименьшего элемента, мы будем понимать под ним иррациональное число.

Таким образом, мы закрываем всю вещественную прямую плотным слоем рациональных и иррациональных чисел, а доопределив среди них отношение порядка и арифметические операции, порождаем совокупный класс вещественных чисел, каждое из которых может быть приближено рациональными числами с любой точностью.

Ценность теории Дедекинда в том, что им на основе наглядных геометрических соображений была выявлена сущность непрерывности - центрального понятия математического анализа, которое раньше использовали, ссылаясь на очевидность.

Сочинение Дедекинда до сих пор остается одним из самых доступных изложений теории вещественных чисел. Следующая попытка - уже не геометрическая, а конструктивная. Произойдет она почти через 24 года, а её автором будем "гений бесконечности" Георг Кантор. Но это - уже совсем другая история. Спасибо за внимание!

Больше интересной математики в телеграмм - "Математика не для всех"

Задумывались ли Вы когда-нибудь о том, что такое расстояние ? Какими свойствами должна вообще обладать некая величина, чтобы носить такое гордое наименование? Сегодня я расскажу Вам, что понимается под "расстоянием" в математике.

Итак, начнём с рисунка. Вам, конечно, известно, что основой всей математики является теория множеств, ведь из неё можно вывести практически все термины, которыми оперирует царица наук. Расстояние - не исключение. Расставим на бумаге в произвольном порядке элементы произвольного множества X = {A,B,C,D,E}:

Каждым двум точкам из этого множества сопоставим некое отношение (или величину) , которую обозначим греческой буквой ρ. Пара (X, ρ) - в математике называется пространством, а от характера ρ зависит то, каким оно будет. Например, если ρ носит характер метрики, то пространство будет называться метрическим. Но что же такое метрика?

Чтобы назвать отношение ρ метрикой необходимо выполнить три условия, которые называются аксиомами метрического пространства:

Предпоследняя строчка определяет метрику как отображение декартова произведения элементов множества в вещественную ось. Третье условие называется неравенством треугольника, известным всем еще со школьной скамьи. Все аксиомы наглядно показаны на первом рисунке.

Обратите внимание на тонкость: само отношение называется метрикой, а вот результат применения этого отношения (читай, отображение) к двум точкам метрического пространства - расстоянием.

Таким образом, только в пространствах, наделенных метрикой, имеет смысл говорить о расстоянии.

Какие бывают метрики ?

В целом, любое отношение, удовлетворяющее вышеперечисленным аксиомам, имеет право называться метрикой. Самый простой способ задать метрику - это посмотреть на числовую ось:

Все аксиомы легко проверяются:

ρ(A,B) = 0, если A=B.

ρ(A,B) = ρ(B,A).

ρ(A,C) ≤ ρ(A,B) + ρ(B,C) - выполняется в форме равенства.

Таким образом, разница между вещественными числами - суть расстояние, а (R, ρ) - метрическое пространство.

Странно говорить о пространстве на прямой, не так ли? Если смущает, приглашаю на знакомую всем координатную плоскость. Отметим на ней два элемента (точками они, формально, станут после доказательства метризуемости), каждому из которых поставим в соответствие упорядоченную пару (x,y):

Аксиомы метрики для введенного нами соотношения также доказываются. Единственное, что неравенство треугольника уже выполняется в классическом виде, данном миру еще Евклидом.

В математике такое называют метрическим пространством R². Расстояние в нём - это фактически длина гипотенузы прямоугольного треугольника, вычислимая по теореме Пифагора. Множество точек, равноудаленных от данной, является окружностью, а число π ≈ 3,14.

Без потери общности можно сопоставить каждому элементу уже тройку координат, что приведет нас к привычному метрическому пространству R³. Окружность в нём, например, станет сферой.

А теперь давайте определим метрику таким образом, как будто мы не можем перемещаться в пустоте между клеток, а только по линиям координатной сетки:

Для такой метрики, как и для привычной нам евклидовой, все аксиомы выполняются. Пространство с такой метрикой называется манхэттеновским, потому что правила игры в нём очень сильно напоминают передвижение по прямоугольной сетке городских кварталов.

Кстати, в качестве заключения. Окружность – это геометрическое место точек. равноудаленных от данной точки, которая называется центром окружности. Число π – отношение длины окружности к диаметру. Смотрим дальше:

Да, только что я показал Вам, что число π может быть равно 4.

Больше интересной математики в телеграмм - "Математика не для всех"