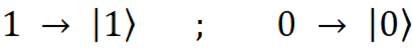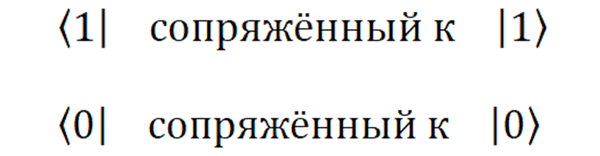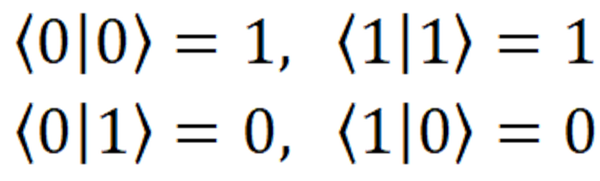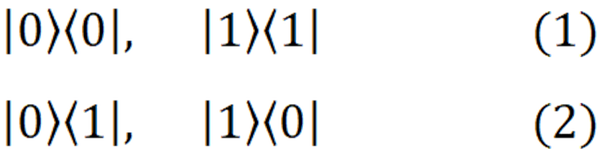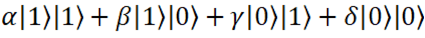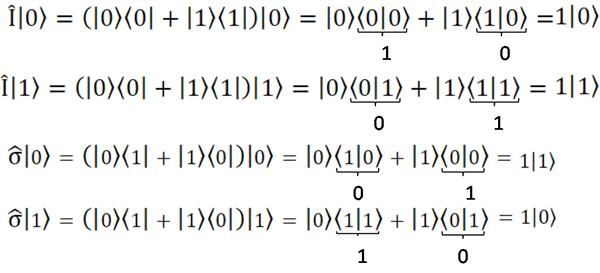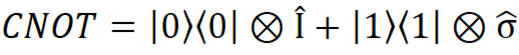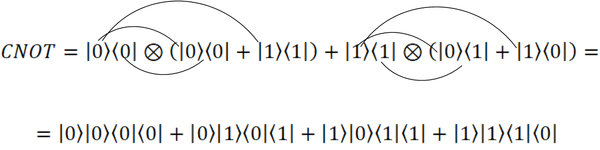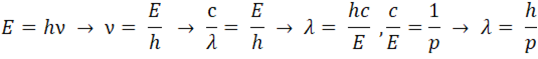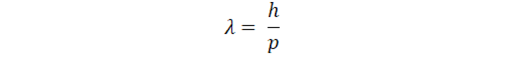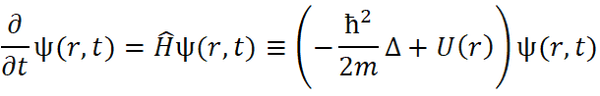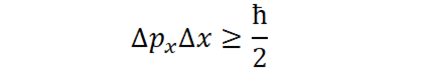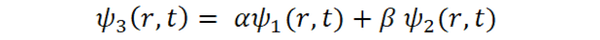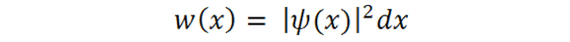Aluatar
Часть 2. Биты, кубиты и прочая квантовая информация
И снова здравствуйте! В прошлом посте я криво и с опечатками попробовал рассказать немного про квантовую механику. Вы мои труды вниманием не обделили, спасибо за это. Покритиковали, вопросы позадавали, в общем, пост, что называется, зашёл. Меня попросили добавить мемов и убавить матана. На счёт матана не обещаю, но мемасиков я добавил.
В этом посте я, как и обещал, постараюсь уже чуть менее криво и без опечаток рассказать про квантовую информацию, что в ней есть и для чего она годится. Поехали.
На дворе шёл транзисторный 1980 год. Москва жила спокойной, мирной, застойной жизнью. Идиллию спокойного городского бытия нарушал только один профессор Московского университета, который порывался всё время что-нибудь посчитать. Вот и в этом году он думал, как бы так ловко взять и обсчитать какую-нибудь систему многих частиц и не умереть от старости в процессе. Профессор был прогрессивным, любил всё новое, читал журнал "Техника - молодёжи", а потому предложил изящное и смелое решение: нам нужны квантовые вычисления. Этим профессором был Альберт Эйнштейн Юрий Иванович Манин.
Для чего оно нужно? Давайте разбираться. Для начала поймём, как с тех пор и до наших дней большинство физиков решают численные задачи.
Численный расчёт - приближённое решение математической задачи путём арифметической работы со значениями функций - числами. Численный расчёт можно выполнить несколькими способами. Первый - собрать много девушек в одном месте и заставить с помощью таблиц сложения , умножения и счётов вычислять то, что нужно.
Однако это долго, дорого и нудно. Кто захочет считать одно и то же целыми днями? (хотя тогда у них особо выбора не было). Поэтому пришлось человечеству изобрести кое-что получше комнаты с женщинами и счётами (я не сексист и ничего не имею против счётов). Это что-то стали называть ЭВМ. Или компьютер. С тех пор (вернее около 40 лет спустя) жизнь у человечества забила ключом. То, что приходилось делать сотням людей напрягая мозг и тратя нервы, стали делать машины. Ну не чудо ли? Но с первых мгновений существования стало понятно, что у такого вычислителя есть принципиальные ограничения. Поглядим, как сие чудо техники работает и по сей день. Это нужно, чтобы понять, почему квантовые вычисления так всех возбуждают.
Ответственно заявляю, что в области классических компьютерных вычислений я являюсь антиспециалистом, по этому возможно всевозможное косноязычие, неточности , кровотечение в области глаз и разжижение мозга у ИТ-шников
Физическую сторону процесса я опущу, она всем знакома, а если нет, то она легко гуглится. Остановимся на принципиальной схеме. Основой хранения и обработки всего нужного нам с вами, учёным, в компьютере - это регистр. Например такой 4-х битный.
Ну, ясно дело, что нужен он для того, что бы туда что-нибудь двоичное число записать. Например, запишем туда число 2. (в том регистре мы тоже записали кое-какое число, попробуйте определить, какое)
Поздравляю! Мы с Вами почти программисты (нет) (ну кто-то, может, и да, но остальные, включая меня, нет). Чтобы стать совсем программистами, нам надо это число как-нибудь преобразовать, читай что-нибудь повычислять. Например, сложим нашу двойку с чей-нибудь ещё двойкой. (схема очень общая)
Конечно, возможны и другие операции с записанными в регистрах числами, но расписывать я это не буду, тем более, что большинство тут и так лучше меня всё про это знает. Отметим одну очень важную для нас деталь: состояние каждой ячейки (бита) регистра определено в каждый момент времени. Это принципиально для классических компьютеров.
-Ну, вроде, отлично - скажете вы - Что же ещё нужно? Наклепаем таких регистров, сделаем транзисторы меньше, регистры и вычислители больше, распараллелим что-нибудь, ядер побольше напихаем. Живём же?
- Да - скажу я - Живём. Но не полной жизнью, товарищи
Представим теперь, что есть у нас один регистр. Он состоит из 4-х битов (как до этого). Теперь все дружно вспоминаем комбинаторику (или гуглим её) и считаем, что всего различных комбинаций нулей и единиц - чисел то есть - может с четырьмя битами быть 2^4 =16
И правда, если перечислить, это 0000, 0001, 0010, 00... нечего нам казённую память тратить. как мы выясним, её у нас пока не так и много. напомню, что за один такт в регистре может находиться только одно число.
Теперь давайте как-нибудь число в регистре преобразовывать, например, находить значения целочисленной функции y=2*n. Означает это, что нам надо все возможные числа умножить на 2. И что же выходит? Нам надо проделать целых мать их 16 вычислений! Кажется не много? Тем более, битов-то мы уже наплодили, деть некуда. Но теперь представьте, что вычислять нам надо какие-нибудь системы уравнений с 100 неизвестными? Там, я вам доложу, к умножению на постоянную всё не сводится, там надо на сетку пространство разбивать, перебором каким-нибудь или секущими корни искать, девственниц в жертву IT-демону приносить. Не буду приводить расчёты (потому что сам их никогда не делал), но для решения системы 100 (а бывает и больше) диф.уравнений (например, для описания квантовых систем) сегодня может понадобиться 10^7 лет. А для разложения небольшого, всего из 400 цифр, числа на множители, потребуется 10^9 годиков. Как вам такое?
И самое обидное, что как ни старайся, бесконечно увеличивать мощность таких компов не возможно. С одной стороны невозможно бесконечное уменьшение транзисторов, так как на характерных размерах у же в 3 нм проявляются квантовые эффекты и т.н. кулоновская блокада (электрон не может пройти через транзистор, хотя ему уже пора). С другой стороны, бесконечно увеличивать мощности в ширь не только ограниченная скорость сигнала не позволяет, но и ограниченные финансы человечества.
Теперь уже суматошный московский профессор не кажется таким ненужным? Хотя, не станем забегать вперёд. Про квантовые вычисления-то мы не знаем ещё ничего...
И вот, движимые идеей что-нибудь посчитать до коллапса Вселенной, учёные стали думать. В кой-то веки. И придумали они квантовые вычисления. После того, как тов.Манин предложил считать не как в школе учили, а как надо, один сумрачный гений от мира квантов по имени Ричард и фамилии Фейнман предложил первую физическую модель такой ЭВМки. Про неё говорит не будем, ибо это долго и не про то.
Но давайте разберём, как квантовые вычисления устроены и чем они так хороши.
Все же знают, как образовалось слово бит? Кто нет, скажу: оно образовалось от двух слов binary digit (двоичное число, спасибо, вики). Но то в классике, у нас то всё квантовое. Ну, мы же теоретики, а не маркетологи, изощряться не будем. И просто единицу информации в квантовых вычислениях назовём квантовый (quantum) бит, или кубит. О них-то дальше речь и пойдёт.
Как можно догадаться, кубит выполняет в квантовом компьютере те же задачи, что бит в классическом, то бишь служит элементарной ячейкой памяти. Но тут есть принципиальное отличие: если бит может находиться одновременно только в одном состоянии, то кубит, в силу принципа суперпозиции, до того, как мы его померяем, находится одновременно в двух. В этом сила и слабость кубита.
Про силу
Вернёмся к нашим регистрам. Пусть теперь у нас есть 4-х кубитная система
И нам надо проделать с ней операцию. Например, опять вычислить значение функции y=2*n.
И опять тут у нас есть 2^4 = 16 возможных чисел в регистре. НО! Вы же помните, что каждый кубит, пока мы его не померили, находится в суперпозиции, то есть содержит и 0 и 1? И весь регистр, следовательно, тоже находится в суперпозиции, и содержит в себе одновременно 16 чисел. Сразу.
И тут мы подходим к самому вкусному. К квантовому параллелизму.
Так как в регистре записаны все числа одновременно, то проводя над ним операцию, мы преобразуем сразу все числа, которые содержит регистр. Делаем мы это параллельно. Убиваем все 16 зайцев, так сказать.
Это замечательно, но как же его, наш кантовый компьютер, программировать? Проще говоря, как на нём вычислять.
Тут, ребята, буде ещё чуть-чуть матана, кому не интересно, не читайте и сразу переходите к слабостям (Второй мемас после этой записи)
ВНИМАНИЕ! СЛЕДУЮЩИЕ ОБЪЯСНЕНИЯ СОДЕРЖАТ ЭКСПОНЕНЦИАЛЬНО БОЛЬШОЕ ЧИСЛО УПРОЩЕНИЙ, ДОПУЩЕНИЙ И НЕТОЧНОСТЕЙ! ЕСЛИ ВЫ БУДЕТЕ ТАК ОТВЕЧАТЬ НА ЭКЗАМЕНЕ, ВАМ В СУДЕБНОМ ПОРЯДКЕ ЗАПРЕТЯТ ЗАНИМАТЬСЯ КВАНТОВОЙ МЕХАНИКОЙ И ИНФОРМАТИКОЙ!!!
Помните, в прошлом посте мы говорили про состояния и про то, что они бывают базисные? так вот, 1 и 0 - это базисные состояния кубита. Запишем их так:
Эти треугольно-прямые скобочки называются кеты, а если они смотрят в другую сторону, то бра. Их придумал Дирак и они очень удобные, сейчас поймём почему.
К каждому нашему состоянию есть состояние сопряжённое, которое обозначается как раз с помощью бра.
Умножение состояния на своё или чужое сопряжённое справа называется скалярным произведением,и в результате мы получим просто число
Но не надо забывать, что состояния-то у нас базисные, а значит очень хорошие. Хорошесть их в том, что при скалярном произведении на само себя (первые две строки), получается единица, а если наоборот, то ноль
Но что же будет, если умножить состояние на сопряжённое не справа, а слева, то есть вот так?
Это уже называется внешнее произведение, и его результат - это оператор, потому что он производит операцию(в том числе и над нашими кубитами). Причём такое умножение на само себя, как в строке (1) даёт эрмитов оператор, то есть хороший, а произведение, как в строке (2) даёт, вообще говоря, неэрмитовый оператор, то есть не очень хороший.
Теперь нам осталось выяснить, чем же так хороши эти Дираковские обозначения? А тем, что они позволяют избегать матриц, интегралов, сверток, комплексной записи и много чего ещё.
Замечательно, мы овладели основами мат.аппарата квантовой механики и информатики. Теперь давайте уже вычислим чего-нибудь?
Представим теперь систему из двух вторых кубитов с помощью уже понравившихся нам обозначений
Здесь представлены все возможные состояния двух кубитов. Откуда взялись альфы и пр. - смотри прошлый пост, принцип суперпозиции.
А теперь составим простую логическую схему. Например: возьмём оператор, умножающий всё на единицу I, и оператор, превращающий нулевое состояние в единичное, а единичное в нулевое σ. На языке базисных состояний это выглядит так
Теперь возьмём два первых кубита, развернём их носами друг к другу, причём единицу к единице, а ноль к нулю. К нулям справа мы приставим I, а к единицам σ. Получим двухкубитный вентиль или гейт Control NOT (CNOT). Он и будет преобразовывать наши два последних кубита
Крестик в кружочке означает тензорное произведение. Тензорное произведение можно очень просто выразить через наши нули и единицы
Ну, теперь совсем всё просто и понятно. Видно, что наш CNOT - это такой вентиль, который содержит два входи и выхода. Один кубит (первый) - контролирующий (control), если он равен нулю, то второй кубит - контролируемый - остаётся таким же. А если контролирующий кубит равен 1, то контролируемый меняется на противоположный (операция NOT), потому вентиль так и называется: Control Not. Действительно, если у нас состояние
|0>|1>, то при умножении слева оно даст нули со всеми слагаемыми, кроме
|0>|1><0|<1|. Можете повычислять ради интереса остальные возможные двухкубитовые состояния. Я только отмечу ещё, что для того, чтобы построить любую логическую схему, достаточно вентиле CCNOT - то же, что и CNOT, только там два контролирующих кубита.
Ну я вас всех окончательно поздравляю! Теперь мы не просто программисты, а квантовые программисты! Ура, товарищи!
Обрадовались уже? А рано.
Про слабость
Принцип суперпозиции нам помог всё быстро посчитать. И он же, а точнее вытекающее из него свойство декогеренции, не позволит нам результаты из регистра извлечь.
Что такое декогеренция? Это то самое разрушение состояния квантовой системы при измерении. Ведь что бы нам узнать, что в итоге получилось, нам надо померить состояние регистра. А регистр-то квантовый, а значит как только мы один раз его померили, получив при этом одно число, мы навсегда избавились от остальных чисел, которые в нём были до измерения. То есть, сколько бы мы дальше регистр не мерили, получать будем одно и то же. Вот так. Как это обойти? Никак. Это штука непреодолима (кто-бы что не писал и какая-бы природа за ней не стояла). И что же делать? Зачем нам такой сложный и, главное, дорогой компьютер, если вся его польза съедается какой-то декогеренцией?
А вот съедается, да не до конца. Существуют алгоритмы, которые позволяют решать некоторые классы задач, которые не доступны классическим компьютерам, квантово. Вам уже интересно, что это за алгоритмы?(надеюсь, да). Но это, а так же как реализовать кубиты физически и, надеюсь, о том, как их реализовал товарищ Лукин в своём чуде, в следующем посте.
Часть 1. Про квантовую механику для квантовой информации.
Не так давно был опубликован пост про созданный российско-американской группой учёных первый программируемый квантовый компьютер на 51 кубите. Достижение в области квантовой информации значимое, тема интересная, однако из комментариев видно, что для многих она непонятна, и, хоть направление и молодое, но успело обрасти мифами. В своих постах я постараюсь эти мифы развеять и объяснить, в меру моих знаний (институтский курс КИ на 5 и изучение работ по теме КИ, связанных с областью моих интересов), что за звери такие "квантовая информация" и "квантовый компьютер".
Но для начала стоит рассказать немного про саму квантовую механику. Ей и будет посвящён этот пост. Итак, приступим.
Пара слов об истории вопроса
Совсем без матана, ребята, не получится, так что извините.
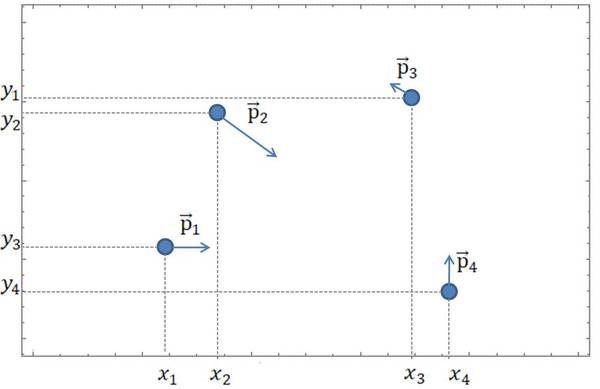
Вообще, для описания любых систем, физики используют состояния. В классической механике, если система состоит из нескольких частиц, то для того, чтобы задать состояние нужно в начальный момент времени t=0 знать координаты и импульсы всех частиц. Внимание на рисунок 1:
Рисунок 1. Система из 4-х материальных точек в момент времени t=0.
Дальнейшая эволюция системы, то есть траектории частиц, их взаимодействия и пр., определяются уравнением (уравнениями) движения. То есть, когда мы "отпустим" все эти частицы, согласно классическим, не квантовым, представлениям, они будут двигаться точно так, как нам предсказал ещё Ньютон в далёком XVII веке.
Но время идёт, наука развивается, человек узнаёт и придумывает разные интересные штуки. Например, лампочка, интересная же штука? Вот и Макс Планк в начале XX века, будучи уже не молодым человеком, решил, что интересная и стал изучать свечение лампочек (на самом деле излучение абсолютно чёрного тела, но там всё рядом). В то время всем казалось, что все законы природы уже постигнуты, и физикам изучать уже, можно сказать, и нечего. Ну подумаешь какие-то небольшие неясности в атомах и микромире, и что-то пока не понятное со скоростью света, ничего прорывного тут не может быть (нет).
Изучал Планк лампочки, долго изучал, и доизучался. Получил он интересный и, как ему, закоренелому классику, казалось, непонятный результат: энергия излучения (и, очевидно, излучателя) обязана делиться на дискретные (прерывистые) порции или кванты. Пользуясь таким своим открытием Планк вывел знаменитую формулу E=hv, а постоянную Планка h он так не назвал, а назвал "квантом действия".
Такое открытие погрузило мировое научное сообщество в бездну уныния и самоанализа. Как это объяснить, никто, казалось, не знал. Никто, кроме Эйнштейна, который, как всегда, всё порешал, но никому ничего не объяснил.
Рассматривая линейные осцилляторы и фотоэффект, Эйнштейн точно понял две вещи: энергия осциллятора может принимать строго определённые дискретные значения (читай, квантуется) и изменяться может только на целое число квантов hv, а электромагнитное излучение (свет в том числе) излучается квантами ( то есть частицами) - фотонами - с энергией, пропорциональной частоте излучения v с угадайте каким коэффициентом. Всё это вылилось в формулу, которую знает каждый школьник (нет, не Е = mc^2, а hv = 1/2*mv^2+A - уравнение фотоэффекта) и нобелевскую премию по физике.
Данный результат вызвал беспрецедентный бугурт у некоторых теоретиков потому что он прекрасно согласовывался с экспериментом, но не нравился им, потому что там были одни ретрограды он не согласовывался с классическими представлениями, к которым все привыкли, все знали и вообще...
В это время работы Эйнштейна читал и вдохновлялся молодой, по меркам РАН, 30-летний учёный Луи де'Блойль. Будучи юным и легковозбудимым, он решил, что раз свет, который раньше считали исключительно волной, оказался ещё и частицей, то почему бы массивным частицам, типа электрона, не быть ещё и волнами? Но раз так, надо бы и длину волны записать! Для фотона всё предельно просто и понятно:
Казалось бы, для массивных частиц всё ещё проще и понятнее: проделываем те же вычисления и получаем то же выражение, только умноженное на два (энергия-то E = 1/2*mv^2), но не тут-то было. Понятно, что формула должна зависеть только от импульса, и быть одинаковой как для безмассовых, так и для массивных частиц. Поэтому из соображений общности (читай, я не буду это выводить, просто поверь мне на слово), де'Бройль записал известную даже дошкольникам (из садика с физико-математическим уклоном) формулу:
Тут научное сообщество просто ох*ело. Квантованная энергия и частицы света - это ещё куда ни шло. Но волны материи?! Несмотря на осторожность де'Бройля в выражениях, на него посыпался град вполне, кстати, закономерных вопросов, главный из которых был "а где в природе это можно посмотреть?".
Первым посмотреть это ("это" - дифракция пучка электронов на кристалле) в природе посчастливилось Клинтону Дэвиссону и Лестеру Джермеру. Всего несколько лет спустя они поставили эксперимент, который теперь заставляют повторять на лабах по общей физике каждого студента. Эксперимент очень знаменит и интересен, но говорить тут о нём я не буду, потому что он, во-первых, заслуживает отдельного поста, а во-вторых, мы же с вами теоретики всё-таки...
- Ну ладно, допустим - сказало научное сообщество - но что с этим со всем делать-то? Все эти волны материи, фотоны, осцилляторы - это замечательно, но мы тут вообще-то природу постигаем, картину мира строим! И как это всё теперь описать, да так, чтоб результаты экспериментов предсказать можно было? Как задать состояние такой частицы, которая ещё и волна? И как узнать, что будет дальше, если Ньютон у микромира не в почёте? Короче, беда и когнитивный диссонанс.
Тут на помощь пришёл забулдыга, пьяница и развратник, примерный муж и семьянин, человек-уравнение и знатный убийца котов радиоактивными изотопами - Эрвин Рудольфович Шрёдингер. Он сверил факты, посидел, потупил, а потом вдруг понял: раз у нас есть частица, которую должна бы описывать механика, но она одновременно и волна, то давайте создадим волновую механику! Логично? Вот и я так думаю.
Сказать-то - это дело не хитрое, но как создавать? Тут Рудольфыч решил пойти по всем известной и проторенной дорожке: написать уравнение движения квантовой частицы. Вот тут-то источники и расходятся: есть разные версии о том, как он его получил, и совсем противоположные мнения о том, в каких это было условиях. Согласно первой версии озарение к нему пришло во время пьянок, оргий и гулянок в швейцарских Альпах, куда он поехал отдыхать от жены. Мол, обложенный коксом и проститутками он чуть ли не на салфетке написал своё уравнение. По второй версии, делал это он дома и глубокой ночью, а когда наконец получил его, то поднялся в спальню к жене (напомню, дело было среди ночи), разбудил её и сказал: "дорогая, мне кажется, я гений". Что ответила жена, история умалчивает. Как бы там ни было, обе байки характеризуют его как мудака человека, способного без видимой причины разбудить кого-нибудь.
Само уравнение можно вывести в две строчки, если знать хоть чуть-чуть вариационное исчисление, но делать я этого, конечно, не буду. Просто напишу его, и вам снова придётся на слово мне поверить.
ОСТОРОЖНО! СЛОЖНЫЙ МАТАН!
Постойте, не стоит материться и добавлять меня в игнор. Из всего, что там написано, нам с вами надо вынести только три вещи: во-первых, надо уважать диффуры, во-вторых ψ(r,t) - волновая функция, она задаёт состояние системы и в-третьих, какое будет состояние у системы в следующий момент времени точно никто не знает, это можно определить только с некоторой вероятностью. Первый удар по классическому определению состояния был нанесён.
Учёные всего мира напряглись. То, что казалось бредом сивой кобылы, начало обретать черты чего-то такого, что может объяснить всё на свете. Но кое-что всё ещё оставалось не понятным, раз мы такие умные, открыли фотоны, сделали волновую механику, то почему бы нам просто не взять и не учинить такой эксперимент, который бы и состояния квантовой системы описал, и, в конце концов, разобрался бы, когда частица - это частица, а когда волна. Тем более, вон у Вильсона что-то с его камерами там интересное есть...
И тут пришёл всем нам известный фашист-математик Гайзенберг, который, кстати, до Эрвина Рудольфыча запилил мат.аппарат для квантов, назвал его матричной механикой, и был в ахуе лёгком недоумении, из-за того, что с этим невнятным уравнением все так носятся, а на его хорошие, милые матрицы никто даже глазком не глянет. В общем, обделили нашего Вернера славой, и он твёрдо решил всё-таки войти в историю науки и всем отомстить.
Рассуждения были просты: если частица - это волна, то траектории у неё нет, ведь какая может быть траектория у волны? Никакой. С другой стороны импульс-то есть? Есть. Значит импульс есть, а траектории, то есть точной координаты в каждый момент времени, нет. Но опять же, как так? Если мы частицу остановим, то вот же она, есть, можете позапускать электроны в люминесцирующий экран да поглядеть на красивые такие вспышки. И координата у неё померена, всё же отлично! Но теперь мы импульс у неё не угадаем. И правда, вот летела она, летела, попала в датчик. И датчик сказал: частица вот тут есть! "а какой импульс у частицы?" - спросите вы у датчика (пусть это будет датчик со встроенным ИИ) - "хз" - будет его ответ (не спрашивайте почему, так устроена природа). Ну раз дело такое, то так и запишем: координата и импульс одновременно не могут быть измерены одновременно и точно. Можно либо одновременно и неточно, либо точно, но неодновременно. Такие дела. Насколько точно одновременно можно эти (и другие не коммутирующие) величины померить, посчитайте из неравенства
Ну всё, классическое понимание состояния системы убито. Убито контрольным в голову. Стоит ли говорить, что Гайзенберг был собой очень доволен? Однако, самое интересное только начиналось. После публикации его работы научная дискуссия по поводу "физики микромира" переросла в настоящий срач, сопровождавшийся отменными шутками и Нобелевскими премиями. Этот срач даже получил своё очень ёмкое название. Назвали его квантовая механика.
Основные принципы квантовой механики
В предыдущей части было очень много букв и совсем мало матана. Тут его, матана, будет побольше.
Начать надо с того, что измерение всегда разрушает квантовое состояние. Всегда. То есть померить одну и ту же квантовую систему с его уникальным состоянием можно только раз. Почему? А потому что измерять мы будем микроскопические вещи макроскопическими приборами, причём ужасным и варварским способом. Представьте, если бы Ваше место положения определяли не аккуратно рулеточкой, а, например, скинув на Вас гигантский астероид (как это определит место, что я несу?), а другого способа посмотреть, где Вы находитесь, нет, потому что у вас вроде импульс есть, мы его примерно знаем, а значит точно установить Ваши координаты просто так не выйдет. Вот примерно то же делают с электроном, только его сталкивают с каким-нибудь датчиком, который минимум в 10^16 больше него. Как тут сохранить состояние? Отсюда можно сделать вывод, что до измерения система может находиться в любом доступном ей состоянии. В каком - мы не знаем.
Ну а теперь о законах. Первый и главный (с точки зрения школы теорфиза Ландау) принцип квантовой механики я уже отчасти описал. Но, как говорится повторение - мать учения, тем более, что в современной редакции он звучит несколько иначе: Всякая пара измеряемых величин, операторы которых не коммутируют не может быть одновременно и точно измерена. Думаю, стоит тут немного прояснить ситуацию. Первое - измеряемые величины - это такие, которые можно получить непосредственно из эксперимента. Ну, это я думаю, понятно. Второе - что значит "операторы которых не коммутируют"? Вот это уже сложнее. Тут нужно знать только то, что одновременно точно не измеримы не только импульс и координата, но и некоторые другие величины, например проекции спина на разные оси. то некоторые-таки одновременно померить можно. Поэтому в квантовой механике для того, чтобы задать состояния используют тройки измеримых одновременно величин. Например
Второй и главный (с точки зрения школы теорфиза Боголюбова) принцип квантовой механики - это принцип суперпозиции. Как мы с Вами выяснили, состояние квантовой системы определяется волновой функцией ψ(r,t), получающейся из уравнения Шрёдингера. Но дела обстоят так, что система может иметь и другое состояние. Кроме того, так как, как мы сказали, каждое следующее состояние в каждый следующий момент времени мы можем предсказать только с определённой вероятностью, то даже зафиксировав в начальный момент времени какое-то одно, потом мы одновременно будем иметь несколько. А раз так, то проделываем такой трюк: пусть у нас есть функция ψ1(r,t), которая удовлетворяет данному Шрёдингеру (для краткости буду так называть уравнение) и задаёт состояние системы. Пусть таким же условиям удовлетворяет функция ψ2(r,t). Тогда верно и то, что сумма этих волновых функций, помноженных на некоторые коэффициенты, тоже является волновой функцией этой же системы. Математически это выглядит так:
Поздравляю, теперь мы с вами можем выражать одни состояния через другие. Но бывают и такие состояния, которые, ну как не пытайся, не выразить через сумму других. Такие состояния называют базисными, а полный их набор, соответственно, базисом.
Но теперь перед нами встаёт вопрос, если и всякие там физические величины мы не предсказываем точно, а угадываем с некоторой вероятностью, то как эту вероятность определить?
Вот тут мы подошли к ключевой вещи в современных квантах, к Копенгагенской интерпретации квантовой механики. В далёком 192 году Нильс Бор и уже знакомый нам Вернер Гайзенберг решили... Они там много чего решили, нам важно только то, что они сказали о волновой функции. А сказали они, что волновая функция, вернее квадрат её модуля, - это и есть вероятность обнаружить систему с такими значениями величин. Например, вероятность обнаружить частицу в пределах малого отрезка dx
Ну а вероятность того, что система будет аз всех возможных состояний находиться конкретно в этом равна квадрату модуля коэффициента перед ней. Например, из описанных выше двух состояний αψ1(r,t) и βψ2(r,t), вероятность обнаружит состояние ψ1(r,t) равна |α|^2.
На этом пока всё. Знаю, что сумбурно, знаю, что не сразу понятно. Если есть вопросы или критика, пишите в комментариях, постараюсь ответить. Следующий пост будет про основы квантовой информации и квантовых вычислений.
Про митинг со стороны равнодушного гражданина
Позавчера собрался я в честь Дня России, да и просто для общего развития, сходить на фестиваль реконструкторов на Тверской. Историей я интересуюсь, погода обещала быть приятной, в общем одни плюсы я видел в такой прогулке. Про намерения оппозиционных граждан провести митинг я, конечно, слышал, но тогда все говорили, что пройдёт он на согласованном проспекте Сахарова, так что я не волновался об этом.
Первый сюрприз ждал меня утром, когда в новостях я прочитал о призыве гражданина Навального пройти по несогласованной Тверской. Этим фактом я, конечно, был огорчён. Во-первых, это явно помешало бы простым гражданам, и мне в их числе, насладиться выставкой под открытым небом; во-вторых, идеи внесистемной оппозиции и Навального мне не близки и стать невольным участником их собраний, тем более незаконных, мне не хотелось. А вся эта ситуация с переносом митинга в несогласованное место под надуманным предлогом вообще выглядит как провокация. Но что делать, не сворачивать же из-за этого планы! Рассосётся как-нибудь, подумал я и уверено, хоть и не без опасений, пошёл.
Вторая на очереди неприятная неожиданность меня встретила уже на месте. Недалеко отойдя от метро я упёрся в толпу людей, некоторые были с плакатами, кто-то выкрикивал лозунги (или ругался было не разобрать). Очередь была объяснима, впереди рамки, граждан внимательно осматривали. Ну, я человек терпеливый и торопиться некуда, решил, что подожду. Через некоторое время и позади меня образовалась существенная такая очередь, люди стали толкаться и теснить друг друга. Казалось, что я в будний день в 9 часов в вагоне метро. Но хуже всего то, что то тут то там стали группами выкрикивать лозунги в духе "Путин - вор", "Россия будет свободной" и пр. Полиция в стороне тоже не стояла, орала что-то про нарушение правопорядка. Вскоре где-то справа от меня довольно внушительное число человек начало скандировать что-то про "Димона", а полиция перешла к задержаниям. Особо вслушиваться в лозунги я не стал, так как был занят поиском способов покинуть сие мероприятие. Вот тут-то меня встретил самый неприятный сюрприз. Выхода из толпы нет. Вообще. Люди стоят друг к другу так плотно, что протиснуться нельзя. Назад тогда ещё никто не шёл, а рамки пропускали на столько медленно, что, казалось, там глухая стена. Вокруг было куча недовольных ситуацией людей. Возникали перепалки между оппозиционерами и простыми посетителями выставки. Периодически с права нас всех теснили "не там митингующие", старающиеся уйти от задержания. Постепенно разочарованные всем этим горожане, так и не попавшие на выставку, стали расходиться, разрядив толпу, чем я и воспользовался.
В связи с этим у меня куча, видимо риторических, вопросов к митингующим и их единомышленникам. Главный из них: ПОЧЕМУ БЛ*ТЬ, ПОЧЕМУ ВЫ НЕ ПРОВЕЛИ СВОЙ, ТОЛЬКО ВАМ ИНТЕРЕСНЫЙ МИТИНГ В СОГЛАСОВАННОМ БЛ*ТЬ МЕСТЕ, А ПОПЁРЛИСЬ ТУДА, ГДЕ ВАС ГАРАНТИРОВАННО НЕ ПОЛЮБЯТ, НЕ ПОЙМУТ И, ВЕРОЯТНО ЗАДЕРЖАТ? Вам так нравится кататься в автозаке? Или вам просто людям нравится досаждать? Неужели вы надеялись постояв у рамок пару часов побороть всякое плохое и создать всякое хорошее? И почему из-за вас простые граждане, в том числе с детьми, должны против своей воли жертвовать своим временем и нервами, даже будучи с вами несогласными?
Цыганята
На волне постов про цыган вспомнилась мне одна история из детства.
Было мне лет 10, занимался я карате (тогда это было дико модно). Летом наш клуб устраивал что-то вроде "детской дружины": на целый день родители отправляют своих чад в секцию, где они тренируются, играют, закаляются - короче полезными вещами занимаются. Ходил туда и я. Но однажды, то ли из-за соревнований, то ли ещё от чего, отпустили нас на пол дня раньше (родители были предупреждены). Ну, чтоб не скучать, компанией из 7-8 человек мы решили завалиться к нашему товарищу домой в гости. Жил он не в самом приятном районе и, что самое главное, там был рынок, а на рынке водились цыгане. Но об этом тогда особо никто не волновался.
Пошли мы к товарищу, а по пути решили закупиться разными снеками, чипсами и пивком колой. Всей оравой зашли в магазин, стали затариваться (каждый сам на себя). Получилось так, что первым всё купил из магазина вышел я и встал у входа в магазин, выходящий прямо на рынок, в ожидании друзей. Тут слышу за спиной: "Эй парень, купи телефон!". Оборачиваюсь и вижу цыганёнка, держащего в руке телефон, что-то вроде мотороллы. Надо сказать, что взгляд у него был нисколько не жалобный, а скорее наоборот, наглый, как и его оклик. Разумеется, я отказал. Но через некоторое время я снова услышал его: "Эй, покупай давай!". Ну, думаю, огребёшь сейчас, не даром же в карате хожу. Оборачиваюсь и вижу уже трёх цыганят, все примерно моего возраста, но у одного из них в руках здоровенная такая цепь. В подробности вдаваться не стану, скажу только, что намеревался разговорами да прибаутками время потянуть, дожидаясь друзей из магазина, но вышло это не очень удачно. Завязалась короткая драка, в ходе которой мне перепало цепью по голове (до крови). Однако сходу меня побить у них не получилось, а тут из магазина вышел один из наших и, увидев картину, завопил: "ДО *username*-А ДОКОПАЛИСЬ!!!11!". Ну, разумеется, выбежала вся толпа школо-каратистов, завязалась потасовка, которая была, из-за массовости и воплей, по видимому, бабушки цыганят быстро разогнана. Мы, испугавшись бабули, её проклятий, и моей окровавленной головы побежали к другу, где меня отмыли. Рана оказалась совсем пустячной, но я очень боялся, что мама будет ругаться, так что мы договорились засекретить этот инцидент. Не знаю насчёт родителей пацанов, а мои, на сколько я помню, в неведении до сих пор.
P.S. С тех пор я ненавижу цыган.