При этом у нее нет не то чтобы мозга, а хотя бы намека на самую примитивную нервную систему. Разрезанная на части, она снова сольется в единый организм, а если части разнести друг от друга, они будут функционировать как отдельные вполне полноценные особи. Такое невозможно, воскликнете вы, и... будете неправы – мать-природа круче любой фантастики.
Знакомьтесь, Physarum polycephalum – не животное, не растение и даже не гриб. Простейшее одноклеточное амебовидное существо.
Ну и что с этого, где же обещанные суперспособности?
Дело в том, что обычная амеба с гаплоидным (одинарным) набором хромосом – это лишь первый этап жизни нашего сверхъестественного приятеля. По сути, это лишь половая клетка в поисках партнера для слияния. Хотя ведет она себя как самая обычная хищная амеба, ползает и лопает все подряд. Вот только размножаться она сама по себе не может.
Впрочем, нашей с вами амебе не придется долго трудиться в поисках полового партнера, ведь ей подойдет любая особь противоположного "пола" с другим набором хромосом, а это 719 вариантов из 720 возможных. Иначе говоря, у этих амеб 720 разных "полов", в отличие от человека, у которого их всего два. Нам с вами куда как сложнее чем ей, ведь она получит отказ от партнера лишь в одном случае из 720.
Найдя пару, амебы сливаются в половом экстазе, образуя принципиально новое существо – плазмодий с полным (диплоидным) набором хромосом. Вот теперь только и начинается полноценная жизнь нашего сверх-существа. Оно начинает носиться в поисках пищи, жрет что ни попадя и быстро растет в размерах.
Что делает амеба, когда ее размеры достигают критического размера? Правильно, делится пополам.
Но плазмодию плевать на обычаи амеб, ядра плазмодия начинают делиться и остаются внутри единой клетки, образуя все большее по размеру ОДНОКЛЕТОЧНОЕ многоядерное существо.
Согласно книге рекордов Гиннесса самый большой Physarum polycephalum достигает размера 5,54 квадратных метра. И это все – одна большая клетка!
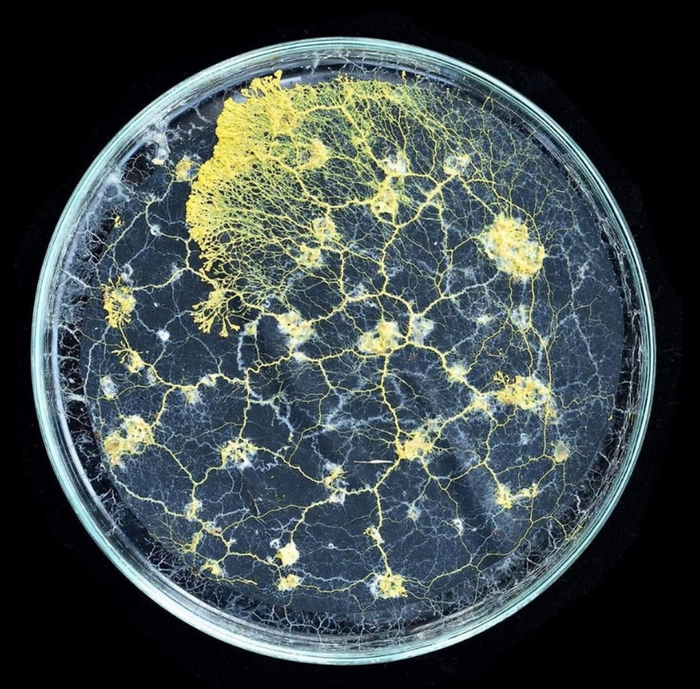
Плазмодий представляет собой двигающийся веерообразный фронт и следующая за ним сеть разветвленных трубочек, напоминающие кровеносные сосуды. На этой стадии он имеет желтоватую окраску. Наше существо способно активно двигаться, плавно перетекая из места на место.
Даже разрезанный на части плазмодий не погибает, каждый его кусочек продолжает жить вполне полноценной жизнью, но при встрече обязательно сольется вновь в одно единое существо.
Если среда слишком сухая или холодная плазмодий меняет тактику, он высыхает, образовав сухой и твердый склероций. В таком виде наш приятель продержится весьма долго – вплоть до нескольких месяцев и даже года, но как только станет влажно и тепло склероций вновь превращается в подвижного плазмодия.
А что делает плазмодий, когда не хватает пищи?
А что делаете вы сами? Дайте угадаю, точно не то, что делает в этом случае плазмодий. Последнее о чем подумаете вы в такой момент – размножение, но именно в этот момент он начинает усиленно размножаться, формируя в своем теле спорангии и образуя в них споры, вплоть до самой своей смерти. Споры же, в свою очередь, чрезвычайно устойчивы к большинству внешних факторов и могут оставаться в состоянии покоя до нескольких десятилетий, пока условия не позволят им прорасти и образовать новые гаплоидные клетки-амебы .
Миксомицеты, к которым сейчас относят Physarum polycephalum, это существа не являющиеся ни животными, ни растениями, ни грибами. Первоначально их отнесли именно к грибам, но способность передвигаться и отсутствие хитина в межклеточных стенках явно указывает на ошибочность такого мнения. Теперь их уже никто не считает грибами, хотя внешне они напоминают обычную плесень, удивительным образом способную двигаться.
Обладают ли наш плазмодий разумом, не имея ничего, хотя бы отдаленно напоминающее мозг?
В 2000 году японский ученый Тосиюки Накагаки поместил разрезанные куски плазмодия в лабиринт, где на выходе и входе разместил еду. Плазмодий стал разрастаться заполняя все ответвления лабиринта, пока не соединился вновь и не добрался до еды. Дальше произошло удивительное – всего через четыре часа плазмодий начал оптимизировать свою сеть сосудов. Тупики освобождались от сосудов, а в направлении еды они утолщались, еще через четыре часа плазмодий сформировал единый витой сосуд по наикратчайшему пути между двумя источниками еды. Ученый сделал вполне логичный вывод, что наше существо, пусть неосознанно, но в итоге выбирает самый короткий путь, оптимизируя свои затраты на получение пищи.
И тут впервые прозвучало утверждение, которое, собственно, и произвело тогда мировую сенсацию: «...одноклеточные создания могут проявлять примитивный интеллект».
Японский ученый, лабиринты и его «разумная» слизь
Плазмодий строит транспортную систему Японии: еда размещена на модели-карте в точках расположения крупных городов Японии. Мы можем видеть,как через сутки плазмодий сформировал сеть, практически совпадающую с дорожной картой Японии. Эксперимент 2010 года.
Плазмодий Physarum polycephalum в дикой природе. Взято с wikimedia
Нам еще многому предстоит удивляться и восхищаться фантазией великого творца – Природы...
Вот такими словами я закончил бы публикацию, если разместил бы ее на каком-нибудь левом развлекательном ресурсе...
Тем, кто не желает напрягать мозги, читать дальше точно не стоит.
..но мы-то с вами люди любознательные, нам мало узнать что-то интересное, лайкнуть и листать дальше, нам просто необходимо разобраться каким образом такое в принципе возможно!
Как примитивное одноклеточное существо не обладающее даже намеком на нервную систему, не говоря уже о мозге, может решать такие сложные задачи?
Давайте рассмотрим для простоты поиск плазмодием еды в лабиринте и нахождение кратчайшего пути ее транспортировки. Мы видим как плазмодий формирует поисковые нити, они постепенно ветвятся, становясь все тоньше, пока не заполнят весь лабиринт. После этого, обнаружив еду, поисковые нити из пустых тупиков начинают втягиваться в основную нить, которая и будет кратчайшим путем к источнику пищи.
Вполне очевидно, что плазмодий обладает "памятью", что позволяет ему не обыскивать раз за разом те места, где он уже побывал, т.е., он их каким-то образом "помнит". Но разве одноклеточное существо может запоминать структуру лабиринта?
Нет, это абсолютно невозможно. Здесь все намного проще: плазмодий оставляет за собой химический след, помечая таким образом места, где уже побывал. Памяти у него как таковой нет, и быть не может. Он просто уже не ищет в тех местах, где чувствует свой след.
Но как же наш безмозглик находит кратчайший путь к еде в лабиринте?
А как вода находит маленькую незаметную дырку в ведре, чтобы из нее вылиться? Вы же не наделяете воду разумом из-за этого. Представим, что ко входу плоского лабиринта (расположен горизонтально и закрыт сверху стеклом) мы подключили шланг с водой. Пусть у нас есть три дыры – выхода из лабиринта на разном расстоянии от входа. Из какого отверстия первым польется вода? Бинго! Конечно же, к которому ведет кратчайший путь!
Однако, читатель тут же укажет, что задача здесь не в нахождении выхода из лабиринта как такового, а в построении оптимального (кратчайшего) пути выхода из него. Та же вода будет литься в конце концов из всех трех отверстий, а вовсе не только из того, к которому ведет самый короткий путь.
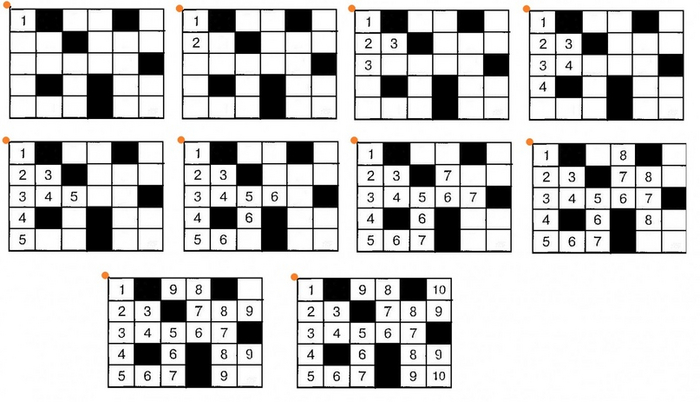
Попробуем промоделировать действия плазмодия на модели лабиринта. Для этого в таблице из верхнего левого угла (оранжевая точка), входа запускаем нашего плазмодия. Первым шагом он заполняет эту самую клетку единицей. Затем двигаясь по вертикали и вбок (возможно движение влево, вправо, вверх и вниз, диагональное движение запрещено), мы заполняем соседние клетки двойкой, что означает, что до этих клеток можно дойти за два хода, затем в соседние свободные клетки проставляем тройки и так далее. Смотрим рисунок ниже.
Хотя мы точно знаем расстояние от входа до нее: восемь шагов (длина нити плазмодия), но сам маршрут пока ни нам, ни самому плазмодию неизвестен. Более того, основное тело еще не в курсе, что какая-то из нитей нашла еду, а потому построить кратчайший маршрут из исходной точки невозможно. Надо начинать с места находки, но как плазмодий может определить куда ему транспортировать еду – ведь весь лабиринт заполнен поисковыми нитями (в нашем случае есть три пути из данной точки), как он определяет ту, по которой ему надо отправлять еду к основному телу плазмодия?
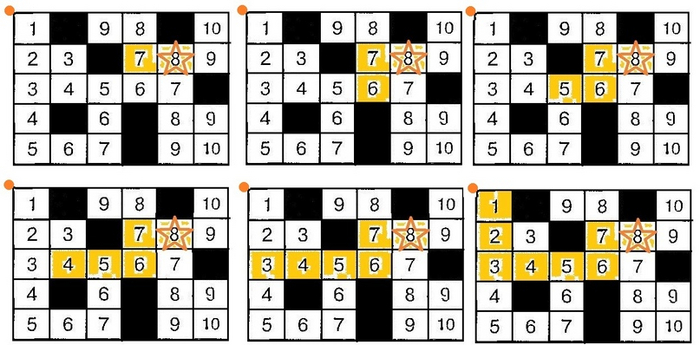
Вспомним как ветвятся поисковые нити, постепенно утончаясь: чем дальше они протягиваются, тем тоньше они становятся. Получается, чем больше число в конкретной клетке лабиринта, тем длиннее, а значит, и тоньше в ней нити. Какое условие выбора направления транспортировки еды по нити использует плазмодий? Он транспортирует еду в ту сторону, где нити утолщаются, куда ее проще направлять, а значит кратчайший путь ведет в ту сторону, где числа уменьшаются.
На самом деле тут изображен не единственный кратчайший путь, на маршруте должны присутствовать два ветвления, впрочем, как и на реальном фото нитей плазмодия в лабиринте выше (Рис.3). Для простоты здесь изображен один путь.
Еда достигает основного тела плазмодия, транспортная нить начинает утолщаться, за счет того, что нити, ведущие из пустых тупиков, начинают втягиваться в нее. И, вуаля! кратчайший путь транспортировки еды к основному телу плазмодия построен.
Таким образом мы смогли понять, каким образом руководствуясь самыми простыми действиями, плазмодий решает весьма сложную задачу.
Разумен ли он при этом? Ответ отрицательный. Хотя его действия кажутся вполне разумными со стороны.
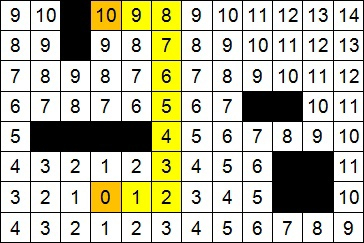
Вот еще один пример решения нахождения кратчайшего пути из одной точки лабиринта (помечена нулем) в другую (помечена оранжевым).
Результат работы волнового алгоритма (ортогональный путь), Взято из Wikimedia
На самом деле наш плазмодий, как многие из читателей уже догадались, реализует классический волновой алгоритм (алгоритм Ли) – алгоритм поиска кратчайшего пути на планарном графе, относящийся к алгоритмам, основанным на методах поиска в ширину. Он всегда дает оптимальное решение, если оно существует, но работает медленно и требует много памяти. Ли его сформулировал в 1961 году, к тому времени наш герой его использовал уже, минимум, полмиллиарда лет.
Вот такие вот дела: оказывается простейшее одноклеточное использует те же алгоритмы, что и мы с вами в поисках оптимальных решений на плоских графах.
Автор Лысый Камрад (LKamrad)
==================================================================================
Так же мои публикации на пикабу можете глянуть в моем профиле. Если вы не желаете пропустить новые публикации, подписывайтесь на автора здесь или на моем личном блоге.
==================================================================================
Вы можете так же поддержать автора деньгами, дабы вдохновить его на новые публикации. Это можно сделать нажав кнопку доната
значок рубля под любой публикацией или по
этой ссылке, если вы с приложения.
==================================================================================