Самые загруженные линии московского метро
Немного о наиболее популярных линиях Московского метрополитена и степени их загруженности.
Моя новая работа...
Когда я пишу сюда пост, мне в первую очередь хочется всегда отблагодарить вас, потому что почти в 30 лет, найти в чем то себя, не мало важно. Если бы не ребята с пикабу, я бы бросила это дело. Хочу благодарить и говорить спасибо.
Кто со мной давно, в курсе, что я переживала до этого и вот сейчас у меня внутри спокойствие.
Эта картина не похожа на остальные, она совсем другая. Как будто у меня биполярное состояние, то я стрессу, то я наслаждаюсь жизнью. Планирую еще походить к психологу ) Но уже к другому )
Зима наверно нагнетает, и вытягивает все силы, как будто порой нехватка серотонина, да и вообще тепла и солнце, ну и наверно поэтому организм начинает сам себя накручивать и стресовать ) Недавно поймала себя на мысли, что живу моментом, ну когда уже будет потеплее, когда можно будет снять всю тяжелую одежду и спокойно ходить , гулять) По моим подсчетам осталось пережить февраль - март, а там уже предвкушении весны ) Обожаю.
Хотя родилась на севере в Мурманске, почему я так не люблю холод не понятно )
П.с. Носочки прекрасные, мне прислали с Норвегии мой уже близкий друг, которого я совсем не знаю ) Спасибо отдельное и за них :)
Ответ Valera.vlz в «Головоломка на пересечение»2
Развели тут теорию графов. Забыв две вещи:
1. Задача школьная, значит решение есть.
2. Если делить отрезки на пересечениях, то на верхней линии будет аж шесть отрезков, а не три, просто комбинаторно, см. примечание ниже.
В целом разбиение отрезков из условий путь тупиковый и по условиям задача (школьная) решается куда проще, если не заниматься усложнением понимания условий.
Поэтому мы имеем единственно решабельное допущение:
- три больших горизонтальных отрезка,
- два больших вертикальных по краям,
- три вертикальных отрезка внутри.
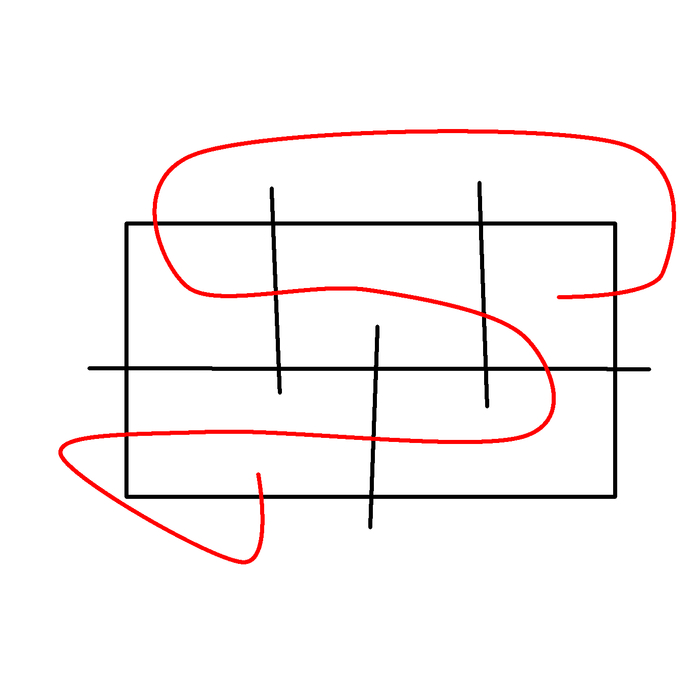
Вот вам специально нарисовал максимально коряво, чтобы было очевидно где у линий конец.
Ну и решение максимально простое:
Условия задачи:Проведите линию через каждый отрезок так, чтобы она не пересекалась, не прерывалась и дважды по одному отрезку не проходила.
Примечание: если считать отрезками каждое разбиение на пересечении, то отрезков сверху вообще-то комбинаторно 6 штук и 2 из них включают в себя третий. Поэтому подобное допущение в принципе не состоятельно.
Точек на отрезке вообще континуум, если между любыми двумя считать отрезок, то их в принципе будет 2 в степени континуум. )
Напоминаю, что задача школьника — решить задачу согласно условиям, а не усложнить до теории графов подзадачу, чтобы доказать нерешаемость при частных условиях.
Ответ на пост «Головоломка на пересечение»2
Задача: провести непрерывную линию так, чтобы она прошла через все линии один раз.
Собственно нашлись те, кто начал искать решение. Но его НЕ СУЩЕСТВУЕТ.
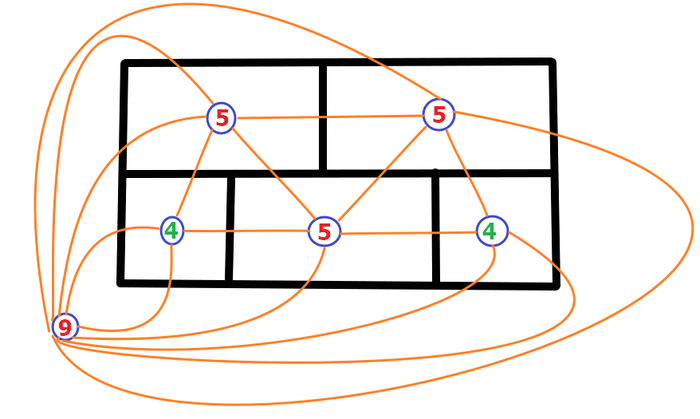
Выше нарисована головоломка, переведенная в графовый вид. Это связный граф (т.е. нет вершин, которые не соединены с другими ребром)
Нам нужной найти Эйлеров путь
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (отсюда)
По теореме:
Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени
Вершина нечетной степени это вершины, у которой нечетное количество ребер. Как видно из рисунка их тут целых 4 штуки, что больше 2. А значит Эйлерова пути не существует и задача не имеет решения.
Логически это объясняется очень просто: вы должны в каждую вершину войти по одному ребру и выйти по другому ребру. Если же количество вершин нечетное, то вы войдете, но не выйдете из такой вершины. Теоретически вы можете из одной вершины выйти (т.е. она будет первой), а в последнюю войти (и не выходить) - в этом случае решение может быть. Но если нечетных вершин больше двух, то задача НЕ РЕШАЕМА.
Карта московского метро всегда должна быть с собой
Источник Москва даром | Новости