Ответ на пост «Головоломка на пересечение»⁠⁠2

Задача: провести непрерывную линию так, чтобы она прошла через все линии один раз.

Собственно нашлись те, кто начал искать решение. Но его НЕ СУЩЕСТВУЕТ.

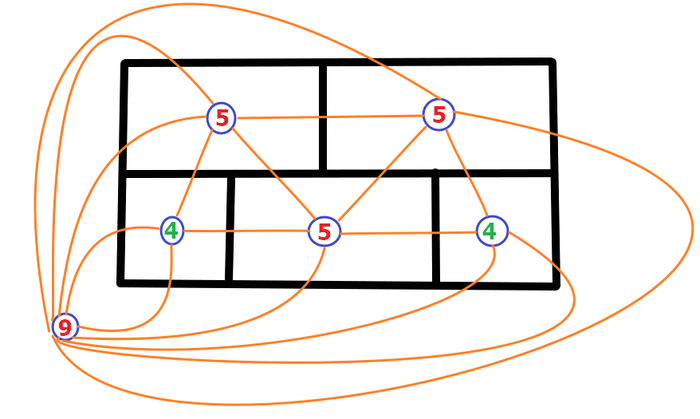
Выше нарисована головоломка, переведенная в графовый вид. Это связный граф (т.е. нет вершин, которые не соединены с другими ребром)

Нам нужной найти Эйлеров путь

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (отсюда)

По теореме:

Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени

Вершина нечетной степени это вершины, у которой нечетное количество ребер. Как видно из рисунка их тут целых 4 штуки, что больше 2. А значит Эйлерова пути не существует и задача не имеет решения.

Логически это объясняется очень просто: вы должны в каждую вершину войти по одному ребру и выйти по другому ребру. Если же количество вершин нечетное, то вы войдете, но не выйдете из такой вершины. Теоретически вы можете из одной вершины выйти (т.е. она будет первой), а в последнюю войти (и не выходить) - в этом случае решение может быть. Но если нечетных вершин больше двух, то задача НЕ РЕШАЕМА.