Ответ Valera.vlz в «Головоломка на пересечение»
Развели тут теорию графов. Забыв две вещи:
1. Задача школьная, значит решение есть.
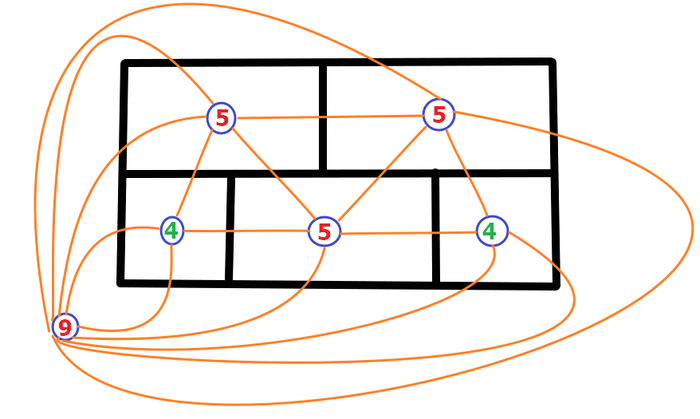
2. Если делить отрезки на пересечениях, то на верхней линии будет аж шесть отрезков, а не три, просто комбинаторно, см. примечание ниже.
В целом разбиение отрезков из условий путь тупиковый и по условиям задача (школьная) решается куда проще, если не заниматься усложнением понимания условий.
Поэтому мы имеем единственно решабельное допущение:
- три больших горизонтальных отрезка,
- два больших вертикальных по краям,
- три вертикальных отрезка внутри.
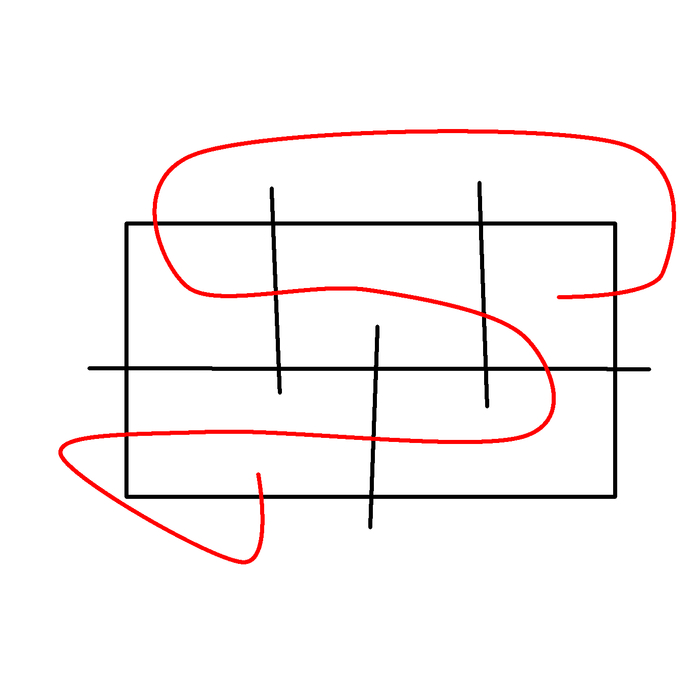
Вот вам специально нарисовал максимально коряво, чтобы было очевидно где у линий конец.
Ну и решение максимально простое:
Условия задачи:Проведите линию через каждый отрезок так, чтобы она не пересекалась, не прерывалась и дважды по одному отрезку не проходила.
Примечание: если считать отрезками каждое разбиение на пересечении, то отрезков сверху вообще-то комбинаторно 6 штук и 2 из них включают в себя третий. Поэтому подобное допущение в принципе не состоятельно.
Точек на отрезке вообще континуум, если между любыми двумя считать отрезок, то их в принципе будет 2 в степени континуум. )
Напоминаю, что задача школьника — решить задачу согласно условиям, а не усложнить до теории графов подзадачу, чтобы доказать нерешаемость при частных условиях.