Произвол судьбы. Про системы счисления и перевод.
Определения и сокращения:
⚫ Н-арный: состоящий из Н частей\компонентов (ун-⇒1, бин-⇒2, терн-⇒3, кватерн-⇒4, ..?)
⚫ Н-ичный: состоящий из Н (един-?\одинарный⇒1, дво-⇒2, тро-⇒3, четвер-⇒4, пятер-⇒5, ..., десятер-⇒10, ...)
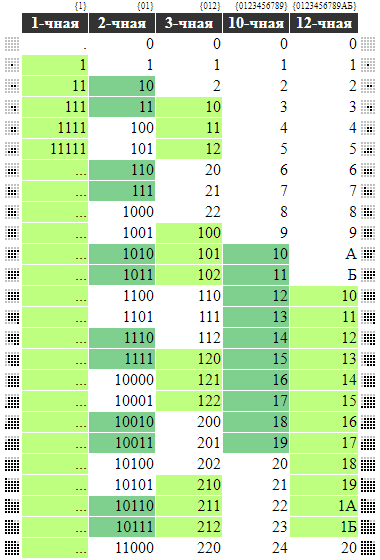
⚫ Системы счисления: 1-единичная\унарная, 2-двоичная\бинарная, 3-троичная\тернарная, ..., 10-десят(ер)ичная, ...
====== ОТ ИСТОКОВ К НАСТОЯЩЕМУ ======
(Вкратце: 111111111111111... ⇒ ...ТТТТСДДДЕЕ ⇒ ...4132 (где ...\Т\С\Д\Е -- условные цифры))
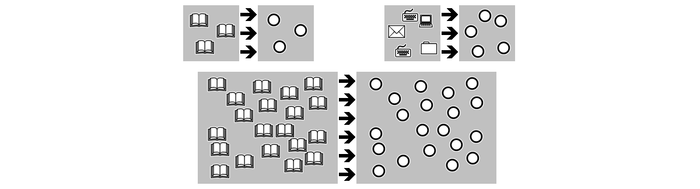
Суть в том, чтобы запомнить\учесть объекты, поэтому их обликом можно пренебречь (см. ниже изобр.).
Но просто так много в уме запомнить не получится, поэтому их лучше приводить в порядок\систему (напр., tally marks) и из этого получается единичная система счисления.
Но записывать ею -- дело трудоёмкое (для отражения 1000 объектов нужно будет 1000 раз написать единицу) и результат занимает много места. Поэтому возникают знаки для обозначения групп единиц. Например, римские цифры: где V=IIIII (5), X=VV (10), L=XXXXX (50), C=LL (100), D=CCCCC (500), M=DD (1000), ...
Но как видно, чтобы экономить место, нужно без конца придумывать новые знаки для больших количеств. Поэтому возникает поместная\позиционная система счисления, где количеству соответствует сочетания\комбинации знаков (см. ниже изобр.) как на велосипедном кодовом замке, на часах со стрелками.
====== ПЕРЕВОД ИЗ ОДНОЙ СИСТЕМЫ В ДРУГУЮ ======
(Сайты для перевода: любая-любая // 10-12 // 2-8-10-16 // 2-10-16 с нулями)
Из названия системы следует, что счёт связан с местом\положением\позицией:
⚫ Теперь вес\масса цифры зависит от её положения в числе (напр., 101 ≠1+0+1, =1Н²+0Н¹+1Нº)
⚫ Поэтому важно знать номер цифры в числе (напр., 752⇒2'1'0, 64.7385⇒1'0'-1'-2'-3'-4)
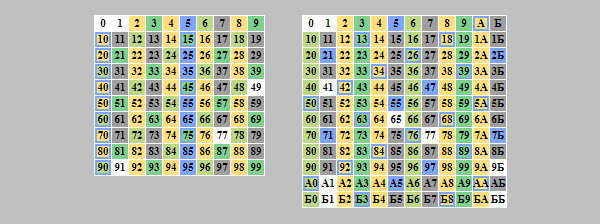
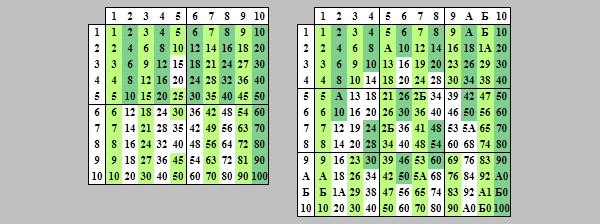
Из той таблицы видно, что одна и та же '10' может обозначать разное количество: 2 (⚁, в 2-чной), 3 (⚂, в 3-чной) , 10 (⚄⚄, в 10-чной), 12 (⚅⚅, в 12-чной). А с точки зрения других систем, 10-чная 10 (⚄⚄) это: '1010' (в 2-чной), '101' (в 3-чной), 'А' (в 12-чной).
Из Н-чной в 10-чную (Н⇒10):
Разложить число на составляющие: цифра×Н^номер + цифра×Н^номер + ... И сложить их.
10⇒10: 201 ⇒ (2Н²+0Н¹+1Нº) ⇒ (2×10² + 0 + 1×10º) = (200+1) = 201
10⇒10: 201.3 ⇒ (2Н²+0Н¹+1Нº)+(3Н⁻¹) ⇒ (2×10² + 0 + 1×10º) + (3×10⁻¹) = (200+1) + (.3) = 201.3
12⇒10: 1А00 ⇒ (1×12³ + 10×12² + 0 + 0) = (1728 + 1440) = 3168
3⇒10: 1001.101 ⇒ (1×3³ + 0 + 0 + 1×3º) + (1×3⁻¹ + 0 + 1×3⁻³) = (27+1) + (0.333+0.037) = 28.37
2⇒10: 1001.101 ⇒ (1×2³ + 0 + 0 + 1×2º) + (1×2⁻¹ + 0 + 1×2⁻³) = (8+1) + (0.500+0.125) = 9.625
Из 10-чной в Н-чную (10⇒Н):
Повторять: число/Н (для целой части), число×Н (для дробной части).
Для наглядности здесь порядок деления будет справа налево, так как при 1-ом делении получается остаток для единиц, при 2-ом -- для десятков, при 3-ем -- для сотен, и так далее. А такой порядок не совпадает с принятым для чисел: сперва идут старшие (весомые\массивные) цифры, потому что, например, разница 301-201 (=100) дороже 103-102 (=1).
Целая часть:
⚫ 10⇒10: 0[2] ⇐ 2[0] ⇐ 20[1] ⇐ 201 (0201)
⚫ 10⇒12: 0[11] ⇐ 11[1] ⇐ 133[4] ⇐ 1600 (01600)
⚫ 10⇒3: 0[1] ⇐ 1[2] ⇐ 5[1] ⇐ 16[0] ⇐ 48 (048)
⚫ 10⇒2: 0[1] ⇐ 1[1] ⇐ 3[0] ⇐ 6[0] ⇐ 12[1] ⇐ 25 (025)
(в квадратных скобках -- остаток, без скобок -- частное; последняя операция необязательна, так как предпоследнее частное закономерно будет последним остатком, если оно меньше Н)
Дробная часть:
⚫ 10⇒10: (0.15430) .1543 ⇒ [1].543 ⇒ [5].43 ⇒ [4].3 ⇒ [3].0
⚫ 10⇒12: (0.120) .12 ⇒ [1].728 ⇒ [8].736 ⇒ [8].832 ⇒ [9].984 ⇒ ... в конце концов должна получиться периодическая дробь.
⚫ 10⇒3: (0.120) .12 ⇒ [0].36 ⇒ [1].08 ⇒ [0].24 ⇒ [0].72 ⇒ [2].16 ⇒ ...
(в квадратных скобках -- целая часть произведения, она как бы остаток).
====== КОММЕНТАРИИ ======
Периодические дроби закономерно появляются, когда делитель нельзя выразить составными элементами Н. То есть если среди составных множителей делителя есть хотя бы 1 инородный элемент, которого нет в Н.
⚫ Например, при Н=10 {2,5} можно выразить 125=5*5*5 (0.008), 50=2*5*5 (0.02), ..., но нельзя 75=3*5*5 (0.1333...), так как '3' нет в составе Н.
⚫ Например, при Н=12 {2,3} можно выразить 36= 2*2*3*3 (0.04), ..., но нельзя 15=3*5 (0.09724...)
В этом плане и есть одно из преимуществ 6\12-чной системы над 10-чной, потому что '3' чаще '5', а значит числа с периодическими дробями реже в ней встречаются. Безусловно, 30\60-чная {2,3,5} ещё лучше, но требует знания 30\60 цифр (!!!), что не кажется разумным\целесообразным\эффективным, ведь все эти цифры должны быть простыми\одинарными и не должны совпадать с буквами. 2\4\8\16-чные одинаковы, так как их Н содержит лишь '2'.
Как и в прошлом посте про преимущества 12-чной системы, здесь могут быть ошибки.