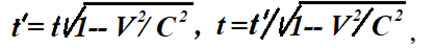Серия «Объяснение парадоксов специальной теории относител»

Из этих положений следуют все парадоксальные выводы СТО, для краткости называемые парадоксами. Мы рассмотрели два парадокса СТО: 1) часы в движущемся объекте идут медленнее (время замедляется), 2) относительность одновременности: два события, одновременные для пилота в космолёте, не будут таковыми для наблюдателя на станции управления на земле (относительность одновременности).  Теперь мы рассмотрим такой парадокс: размер движущегося объекта (по сравнением с неподвижным) уменьшается в направлении его движения. Для простоты пишут, что уменьшается длина движущегося объекта.

За счёт чего уменьшается длина движущихся объектов
Время в движущемся объекте (например, в космическом корабле) по законам СТО замедляется по сравнению с временем в нём же, если он неподвижен. Поэтому на выполнение той же технической операции в движущемся объекте будет затрачено меньше времени, чем в неподвижном. Пусть мы измеряем длину неподвижного и взлетевшего космолёта, например, посылкой радиосигнала вдоль направления его движения ( вдоль его длины) стоящим на земле радиолокатором. В обеих случаях замеряем время прохождения сигналом длины космолёта. Опускаем технические детали. Затем умножаем это время на скорость сигнала и получаем длину космолёта. . При измерении из неподвижного радиолокатора время прохождения длины летящего космолёта будет меньше. Так как скорость сигнала постоянна и одинакова для неподвижного и летящего космолёта, то за меньшее время сигнал пройдёт и меньшую длину. Таким образом получается, что длина объекта при движении будет меньше, чем неподвижного. Уменьшение длины движущегося объекта будет в той же пропорции, что и замедление для него времени. Величина замедления времени (как это установлено в СТО) зависит от скорости движения объекта (например, космического корабля). Чем больше скорость объекта, тем больше будет замедление времени и уменьшение его длины. Вывод формулы длины движущегося объекта приведён в дополнении к посту.

Специалисты по СТО об уменьшении длины при движении
Часть специалистов по СТО считала уменьшение длины объекта реальным. Г. Минковский, сотрудничавший с Эйнштейном отмечал: «Эта гипотеза звучит крайне фантастически. Ибо сокращение должно мыслиться не как результат сопротивления эфира, но как подарок, ниспосланный свыше, как побочное обстоятельство самого факта движения» [2].

Очень оригинально высказывание по этому вопросу известного физика-теоретика Паули. Он указывал, что сокращение длины движущегося тела связано с относительностью одновременности. Поэтому некоторые считают, что сокращение длины только кажущееся явление. Он утверждал:«Мы не считаем, однако, подобное мнение целесообразным, так как во всяком случае сокращение стержня принципиально наблюдаемо» [3, с.28]. Что значит: «... принципиально наблюдаемо?» Правильнее было бы указать, что сокращение вычисляемо (по формулам СТО). Для оценки теории имеет значение – правильное это положение или нет. А вот целесообразно его придерживаться или нет – такая постановка вопроса не логична.
Выводы СТО вначале считали (часто – и сейчас считают) реальными и даже пытались увековечить в архитектуре.

На стене изображено сжатие колеса в направлении его движения, если оно не катится, Написана формула уменьшения размера колеса в направлениях движения, указанных стрелками, в зависимости от скорости. Чем скорость больше тем диск больше сжимается.

Эйнштейн об уменьшении длины движущегося объекта 
Окончательная трактовка этого положения А. Эйнштейном (1915 г.) такова: «Если стержень в покое обладает длиной lн, то при движении со скоростью V вдоль своей оси он будет обладать с точки зрения несопутствующего наблюдателя меньшей длиной… Длина тем меньше, чем больше скорость V движущегося стержня» [4, с. 76]. То есть мнение Эйнштейна о сокращении длины объекта аналогично его мнению о замедлении времени, что это уменьшение, полученное расчётом наблюдателя по формулам СТО, с земли, из другого космолёта, скорость которого отлична от данного и т. д..

Есть ли реальная (абсолютная) длина?
При принятии реальности сокращения длин предметов в зависимости от скорости движения получается полная относительность размеров. Это и отмечается во многих современных учебниках: «Следовательно, не существует никакого абсолютного расстояния, длины или протяженности, так же как не может быть никакого абсолютного времени» [5, с. 84]. При этом возникает вопрос: какую длину считать истинной (на самом деле)? И есть ли она? В современных учебниках утверждается, что такой вопрос неявным образом вводит абсолютную длину, что неприемлемо для СТО.

Какой же размер считать истинным? Тот размер, который постоянен и, следовательно, имеет объективное значение. То есть – это размер в системе координат, в которой предмет находится в покое – собственный размер, как принято писать в СТО [1, с. 68]. Например, в космическом корабле (утрированный пример) провалился пол. Какой длины доски им посылать? При расчёте из разных несопутствующих объектов (из иных космических кораблей и с земли) их длина будет различной. Надо брать длину, которая равна собственной длине в космическом корабле. Это и будет реальная, абсолютная длина. Показать эту длину из движущегося объекта всем остальным специалистам по СТО очень просто: надо повернуть сломанную доску на 90 градусов, чтобы её длинная сторона располагалась поперёк направления движения, так как поперечные размеры объекта в СТО при движении не изменяются.

Что же значит уменьшение длины предмета, становится ли он на самом деле короче? Поясняю это цитатой из Угарова [1, с. 67], одного из основных популяризаторов СТО на научной основе (без упрощения). Для лучшего понимания цитаты поясняю, что ИСО – это инерциальная система отсчёта: любой объект, движущийся равномерно и прямолинейно. «Прежде всего, ясно, что никакого реального сокращения длины линейки произойти не может. Это следует из основного принципа, положенного в основу СТО, – принципа равноправия всех ИСО. Во всех ИСО физическое состояние линейки одно и то же. Поэтому не может быть и речи о возникновении каких-либо напряжений и деформаций, ведущих к сокращению линейки. «Укорочение» линейки происходит исключительно в силу различных способов измерения длины в двух системах отсчёта. Следовательно, реально никакого укорочения нет». То есть для наблюдателя, расположенного в движущемся объекте, уменьшения длины нет.
Выводы
Таким образом, следует признать справедливым заключение А. Эйнштейна как в отношении замедления времени, так и в отношении уменьшения длины, что эти явления имеют место только для наблюдателя из несопутствующей системы. То есть из объекта, имеющего иную скорость, чем тот, в котором мы измеряем длину. При анализе этих эффектов необходимо учитывать, что они являются следствием расчёта размеров и времени на основе формул СТО. А если так рассчитанные параметры только кажущиеся, то это надо иметь в виду. Хотя многие специалисты считают их реальными.

Дополнение: вывод формулы длины движущегося объекта
Время при измерении длины стержня в стоящем поезде обозначим t, в движущемся – t ' (так принято в СТО). Тогда длина неподвижного объекта будет равна скорости света С, умноженной на время прохождения светом его длины.
L= Сt.  (1) 
Длина движущегося объекта тоже равна скорости света С, умноженной на время прохождения светом его длины.
L' = Сt '.  (2)
Но отношение времени в движущемся и неподвижном объекте в СТО:
t '= t √(1–(V/С)^2), откуда  t '/ t = √(1–(V/С)^2),  (3)
где ^2- показатель степени при (V/С), V– скорость движущегося объекта ( космолёта и т. д.).
Из уравнения (1) подставим значение С в (2) и получим, что  L' = L t '/ t.  В это уравнение подставим из (3) значение t '/ t. Тогда L' = L√(1– (V/С)^2).  L' меньше L, так как квадратный корень √(1– (V/С)^2 ) меньше единицы

Использованные источники
1.Угаров В.А. Специальная теория относительности / В.А. Угаров. — М.: Изд-во «Наука», Главн. ред. физ.- мат. лит., 1969.
2.Минковский Г. Пространство и время (доклад).
―URL: https://booksee.org/book/636449
3. Паули В. Теория относительности: Пер. с нем. и англ, — 3-е изд., испр. — М.: Наука. Гл.ред. физ.-мат. лит., 1991. — 328 с. ―URL: https://booksee.org/book/1009051
4.Эйнштейн А. Теория относительности, избранные работы / А. Эйнштейн. —Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000.
5.  Рузавин Г.И Концепции современного естествознания: учебник для бакалавров. Москва: Проспект, 2017.

Рассматриваемое событие
Пусть событиями будет достижение светом передней и задней стенок движущегося вагона от вспышки света в лампе, висящей в середине вагона. Будут ли эти два события одновременны для пассажира в вагоне и для наблюдателя на платформе? Пассажир сидит в центре вагона (под лампой).

Путь света в движущемся вагоне
Вспышку света в центре вагона выполняют, когда наблюдатель на платформе будет против центра вагона, то есть напротив лампы и пассажира. Свет для них включился одновременно. Свет в вагоне идёт от центра вспышки (лампы), движущейся вместе с вагоном. Для пассажира (в середине вагона) передняя и задняя стенки вагона находятся на равных расстояниях от источника света.  И для него свет дойдёт до передней и задней стенок вагона одновременно. Это и так ясно, поэтому я не буду пояснять сказанное рисунком.
Путь света для наблюдателя на платформе
Для наблюдателя 1 на платформе источник света 2 в момент вспышки находится против него (рис. 1, а). И свет движется для него из этой точки 2 с равной скоростью в обе стороны, но уже независимо от движения вагона. То есть свет для наблюдателя на платформе движется уже из неподвижного для него источника, который на рис.1расположен на вертикальной линии, проведённой от наблюдателя на платформе.

Для наблюдателя на платформе задняя часть движущегося вагона приближается к месту (точке) вспышки, а передняя – удаляется от неё. Поэтому свету, движущемуся к задней стенке вагона, надо пройти меньшее расстояние, чем свету к передней стенке вагона. Для него (вид с платформы) вспышка света достигнет задней стенки вагона раньше, чем передней – не одновременно (рис. 1, б). То есть в соответствии с СТО эти события, одновременные для пассажира, будут не одновременными для наблюдателя на платформе.

Дополнение
Для света это представить трудно в связи с его огромной скоростью. Для проверки этого положения, стоя на остановке, мысленно включите на асфальте перед собой два предмета, которые начнут двигаться в разные стороны с одинаковой скоростью (как свет) в момент начала движения поезда. И предмет, который движется навстречу задней стенке, встретится с ней раньше, чем движущийся вперед – с передней.

Выводы
Свет от лампы в центре движущегося вагона дойдёт до переднего и заднего конца вагона для пассажира, сидящего в середине вагона одновременно, а для наблюдателя на платформе не одновременно. В этом и заключается относительность одновременности в СТО.
Разное по времени достижение светом стенок вагона есть только с точки зрения наблюдателя на платформе То есть этот парадокс фактически показывает, что результат для наблюдения из неподвижного объекта не соответствует тому, что происходит в подвижном объекте.
Использованные источники.
Эйнштейн А. Теория относительности, избранные работы / А. Эйнштейн. —Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000.

Содержание поста. Введение. Эйнштейн о ходе часов в 1905 и в 1915 гг. Паули о ходе движущихся и неподвижных часов. Отечественные физики о замедлении времени для движущегося объекта. Трактовки хода часов, противоречащие принятым в СТО. Заключение.

Введение
Этот пост продолжает серию по объяснению парадоксов СТО. В первом посте серии я показал причины разработки СТО. Во втором посте рассмотрел парадокс о замедлении времени в движущемся объекта (на примере поезда и платформы).  Специалисты по СТО трактуют выводы этой теории различно, что необычно для строго научной теории. Об этом и будет данный пост применительно к выводу СТО о замедлении времени. В нём будет много цитат специалистов по СТО. Поэтому я поясняю используемую ими терминологию. В СТО движущиеся и неподвижные объекты часто заменяют системами координат с часами и обозначают как инерциальные системы отсчёта, часто как системы отсчёта и просто как системы. Часто вместо времени используют показания часов.

Эйнштейн о ходе часов в 1905 и в 1915 гг.
В начале разработки СТО (в 1905 г.) Эйнштейн делает вывод о реальности замедления времени для движущегося объекта (движущихся часов) [49, с. 93]. Этот парадокс я описал на примере поезда (движущегося объекта) и платформы (неподвижного). Парадокс состоит а том, что для людей, находящихся на платформе, часы в поезде (рис. 1) отстают от часов на платформе. Время в движущейся системе (для движущегося объекта) замедляется. Так нас учили и учат сейчас, начиная со школы (рис. 1).

Так как все объекты в природе движутся, то неподвижными в СТО считают те, где находятся наблюдатели. Поэтому Эйнштейн вместо неподвижных объектов (систем) вводит понятие несопутствующих систем, которые имеет скорость, отличную от изучаемых движущихся объектов (систем). Их иногда называют условно неподвижными. Позднее (в 1915 г.) А. Эйнштейн предлагает иную формулировку замедления времени:

Но большинство физиков придерживаются первого вывода Эйнштейна, что замедление времени в поезде реально. И это излагается в учебниках по физике, даже по вновь введённой дисциплине «Концепции современного естествознания», а также в научно - популярных изданиях. Акцент во многих случаях делается на достоверности и применимости на практике (без достаточных оснований). Я не цитирую их и не делаю на них ссылок из-за большого числа и доступности таких изданий. Я цитирую известных специалистов, значительно повлиявших на признание СТО как эпохального явления.

Паули о ходе движущихся и неподвижных часов
Известный физик-теоретик Паули (1921г.), несмотря на изменение Эйнштейном трактовки замедления времени, считает замедление хода часов реальным: «Таким образом, часы, движущиеся со скоростью V, при измерении в единицах времени системы К идут медленнее … , чем покоящиеся часы. Это следствие из преобразований Лоренца, неявно содержащееся уже в исследованиях Лоренца и Пуанкаре, было ясно выявлено Эйнштейном» [68, с. 29].

Отечественные физики о замедлении времени для движущегося объекта
Многие отечественные физики считают замедление хода часов для движущихся объектов реальным явлением.
А. В. Угаров аналитически выводит, что замедление времени, это реальное значение времени в движущемся объекте [39, с. 46-48] (например, в поезде). Но после этого: «Следует подчеркнуть, что изменение хода часов, которое мы получили, не имеет ни малейшего отношения к какому- либо нарушению темпа хода часов в той или иной системе» [39, с. 65,71]. То есть разница в ходе часов получается в результате расчётов по формулам Лоренца. Какой смысл тогда в использовании ф-л Лоренца?
Я. П. Терлецкий: «…промежуток времени, отмеченный неподвижными часами, оказывается большим, чем промежуток времени, отмеренный движущимися часами. Но это и означает, что движущиеся часы отстают от неподвижных, т. е. их ход замедляется. …Полученное замедление являемся вполне реальным..» [38, с. 41].

Д.В. Скобельцын одновременно с признанием реальности замедления времени в движущейся системе отмечает: «Если обе системы (А и В) тождественны, то результат такого сравнения точно предсказывается специальной теорией относительности. Каждому из наблюдателей (А и В) представляется (только представляется – замеч. авт.), что время в другой системе «течет» медленнее» [36, с. 166]. Но это представление основано на расчёте по формулам Лоренца.

Трактовки хода часов, противоречащие принятым в СТО
К. Ланцош предлагает формулировку парадокса часов, противоречащую всем, начиная с Лоренца: «Наблюдатель в быстро движущемся поезде смотрит в окно и рассматривает людей на платформе. Он поражен, обнаружив, как быстро они стареют. Сверяя со своими часами, он заметит: «Ну и ну! У них даже борода отрастает за десять минут». Однако обратим этот эксперимент. Кто-то из стоящих на платформе достает свои часы и смотрит за пассажирами поезда. Вы думаете, он скажет: «Как это они умудряются сохранять свою молодость? Они могут не бриться годами и выглядеть свежими!». Ничего подобного. Он скажет: «Черт возьми. До чего же быстро они стареют! Не проходит и десяти минут, как у них отрастает борода!» [22, с. 70]. То есть все процессы в иной системе отсчёта идут быстрее. Время ускоряется, а не замедляется, космонавт стареет быстрее близнеца- землянина.

Применительно к ходу часов К. Ланцош также обосновал совсем иное, чем  другие: «…кажется, что часы в движущемся поезде идут медленнее, чем часы на платформе... В действительности различия в измерениях времени возникают совсем не потому, что часы идут по-разному; часы во всех системах отсчета идут совершенно одинаково» [22, с. 69]. Различия в «течении» времени для движущегося и неподвижного объектов он объясняет тем, что его измерения выполняются в каждом движущемся предмете по мировым линиям, которые представляют собой его путь в четырехмерном пространстве-времени [22, с. 69]. При этом он не указывает, что различие в мировых линиях основывается на признании разного хода часов в поезде и на платформе. Фейнман также считал, что для движущегося объекта всё изменяется в соответствии с СТО, но только из-за изменения масштаба времени [2]. Внешне же (по часам) изменений не заметно.
Заключение
Анализ литературных источников и приведённые высказывания выявляют, что существует различное толкование соотношения хода неподвижных и движущихся часов – замедления времени в движущемся объекте:
1. Время замедляется реально.
2. Время для движущегося и неподвижного объектов не изменяется, изменение получается пересчётом времени по формулам Лоренца.
3.  Имеет место двойственный подход к этому: сначала аналитически выводится замедление времени, через несколько десятков страниц указывается, что это получается из-за пересчёта времени по формулам Лоренца.
4. Часы идут везде одинаково, а время замедляется (Ланцош и Фейнман).
5. Для наблюдателя в любой системе время в иной замедляется.
6. Для наблюдателя в любой системе время в иной ускоряется (Ланцош). Это получается, если источник и приёмник света устанавливать там, где находится наблюдатель. Но ведь расположение и мнение наблюдателя не влияет на реальный характер действия закономерностей.
Из всего этого следует, что:
1. Замедление времени зависит от расположения приборов.
2. Замедление времени противоречит принципу относительности, так как в движущемся и неподвижном объектах ход часов подчиняется разным законам. Поэтому Ланцош и Фейнман явно, а некоторые (после последнего вывода Эйнштейна) мельком утверждают, что часы идут одинаково.
3.Если замедления времени нет, то как можно опытным путём подтвердить то, чего нет?
4.Получается сомнение в объективности вывода о замедлении времени. Но ведь это следует из постоянства и максимальности скорости света, что вроде бы подтверждается и опытным путём, но прямого опыта до сих пор не проведено.

Источники. 1. Ссылки на источники 22, 36, 38, 39, 49, 68 указаны по списку источников в книге «Кузьмин М. В. Объяснение парадоксов. От Зенона до Эйнштейна и далее. – М.: Изд. Бит-принт, 2021».
2. Фейнман Р. Характер физических законов: Пер. с англ. – М.: «Наука», 1987.

Введение. Некоторые понятия
Почему я решил написать серию постов на эту тему? Потому, что выводы СТО считаются парадоксами. А парадоксы – это высказывания, мнения, научные выводы и т. п., расходящиеся с общепринятыми представлениями и поэтому кажущиеся нелогичными и даже противоречащими здравому смыслу. Таковы все выводы СТО. Отношение в обществе (даже в научном) к ним разное: от восхищения до полного недоверия. Многие считают, что СТО очень сложная теория и понять её выводы невозможно. Поэтому я постараюсь доступно изложить, как и что в СТО получается, поясняя это на рисунках. Для желающих в дополнениях будет приведён вывод формул.
В этом посте мы рассмотрим замедление времени (отставание часов) в движущемся объекте.

Что такое движущийся и неподвижный объекты в СТО? Неподвижным объектом считается тот, в котором находится наблюдатель (человек, приборы).  Для наблюдателя на земле (платформе), она – неподвижный объект, поезд –движущийся. Для наблюдателя (пассажира) в поезде неподвижным будет поезд, а платформа –движущимся объектом. Я рассматриваю  поезд – землю как любимый пример Эйнштейна.  Но так как
в природе все объекты движутся, то Эйнштейн вместо неподвижный часто употребляет термин несопутствующий объект.  Это такой, по отношению к которому объект движется с определённой скоростью. Например, другой поезд.

1.  Объяснение  парадокса о замедлении времени для движущегося объекта (поезда)
1.2. Неподвижный объект – платформа, подвижный – поезд  
На платформе находится наблюдатель (рис.1). Тогда источник и приёмник короткого светового сигнала (импульса) ставят в движущемся поезде: источник – на полу вагона, над ним (на потолке) – приёмник. Путь светового сигнала от источника до приёмника в движущемся поезде – вертикально вверх со скоростью света. За счёт движения поезда относительно платформы этот световой сигнал (светящаяся точка) для наблюдателя на платформе (человека или по экрану) будет двигаться по наклонной линии, которая будет длиннее пути в поезде. Скорость движения сигнала по ней будет равна тоже скорости света (но не более), так как скорость света в СТО есть наибольшая возможная скорость движения.  При движении с равными скоростями меньший путь (в поезде) будет пройден за меньший отрезок времени, чем на платформе. Значит часы в поезде идут медленнее и постепенно будут отставать от часов на платформе всё больше и больше. То есть время в поезде будет замедляться.

На рис. 1 показаны пути света от испускания до приёма светового сигнала: В поезде 1 – вертикально вверх, относительно платформы 2– по наклонной линии за счёт движения поезда, который пройдёт путь 3 – пока свет проходит путь 1 до приёмника.

Вот мы и выяснили без формул, как в СТО получают замедление времени для движущегося объекта (поезда). Насколько оно замедляется, можно определить расчётом из Δ АВД по теореме Пифагора (расчёт – в Дополнении). Поэтому в 1905 г. в результате разработки СТО А. Эйнштейн делает вывод о реальности замедления времени для движущегося объекта (часов) [1, с. 93]. Время в поезде при таком (как на рис. 1) ∆ АВД будет составлять примерно 0,6 от времени на платформе. Такое соотношение времён будет примерно при скорости поезда =201 000 км в секунду. Такие большие скорости называют релятивистскими. При движении в земных условиях замедление времени не ощутимо.

1.2. Неподвижный объект– поезд, подвижный – платформа
Для пассажиров неподвижным будет поезд, а платформа –движущимся объектом. Для наблюдателя в поезде платформа будет двигаться со скоростью поезда в обратном направлении. Световой сигнал относительно платформы пойдёт вертикально вверх, а относительно наблюдателя в поезде – по наклонной линии. Всё будет наоборот: замедление времени – но уже на платформе, а не в поезде.

2. Вывод. Парадокс зависит от наших действий
Но в реальных условиях (независимо от наших определений, и установок источника и приёмника света в разных местах) ничего не изменилось.Получается, что замедление времени будет там, где нами расположены источник и приёмник света. Но это лишает вывод о замедлении времени объективности. К тому же часы в поезде и на платформе не могут одновременно показывать разное время для разных наблюдателей (для пассажиров и людей на платформе), если они выполняют сверку часов одновременно (а в СТО должны). В СТО этот парадокс (иногда) обходят заключением, что наблюдателю в поезде представляется, что время замедляется на платформе, а наблюдателю на платформе – что в поезде [2, с. 166]. Что значит представляется? Каждый из них определяет время для другого расчётом по формулам Лоренца.

Изменение Эйнштейном вывода о замедлении времени
Вероятно, по этим и иным причинам А. Эйнштейн (в 1915 г.) предлагает иную формулировку замедления времени: Движущиеся часы идут (с точки зрения наблюдателя из неподвижного объекта) медленнее, чем те же часы, если бы они покоились. И любой процесс в движущемся объекте (системе) замедляется, если он приводится в поступательное движение. Но это замедление происходит только с точки зрения наблюдателя из неподвижного объекта [1, с. 77]. Дословные цитаты – в следующем посте.

Но ссылка на точку зрения наблюдателя из неподвижного объекта скрывает серьёзное, но замаскированное изменение смысла СТО. Здесь определяющее слово только. На это надо обратить внимание. Это значит, что при расчёте с платформы по формулам Лоренца в поезде замедление времени есть, а на самом деле его нет. И на платформе (при расчёте из поезда) замедление времени есть, а реально (по часам на платформе) тоже нет. Это свидетельствует о признании Эйнштейном того, что для движущегося объекта время не замедляется. То есть замедление времени для движущегося объекта (системы) в реальных условиях отсутствует. Но этот факт остался не замеченным (?) и не принятым во внимание (!) большинством специалистов по СТО. Поэтому в следующем посте рассмотрим странное явление в науке– различное толкование специалистами основного положения развиваемой ими теории – замедления времени. Об экспериментальных проверках выводов СТО – в последнем посте этой серии.

Дополнение. Вывод уравнения Лоренца
На рис.2, б показан вывод формулы замедления времени для движущегося объекта: С–скорость света, V– скорость поезда, t – время по часам на платформе, t'– время по часам в поезде. В СТО параметры движущегося объекта отмечают штрихом. В Δ АВД расчёт длин АД и АВ ведут по часам на платформе t, расчёт длины ВД – по часам в поезде t'.

Использованные источники
1. Эйнштейн А. Теория относительности, избранные работы / А. Эйнштейн. –—Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. 2. Угаров В.А. Специальная теория относительности. – М.: Изд-во «Наука», Главн. ред. Физ.- мат. лит., 1969.  Подробнее: Кузьмин М. В. Объяснение парадоксов. От Зенона до Эйнштейна и далее. – М.: Изд. Бит-принт, 2021.

Обращение к читателям
Я начинаю публиковать серию постов по анализу специальной теории относительности (СТО), выяснению причин парадоксальности её результатов, а также объективности выводов. Сейчас по этим вопросам имеется много публикаций. В большинстве публикаций для широкого круга читателей имеют место чрезмерные упрощения и примитивные аналогии, В которых указания на реальность выводов СТО, а также критические замечания в её адрес зачастую являются недостаточно обоснованными.
Поэтому я решил написать серию постов, в которых будут изложены положения и выводы СТО с последующим анализом и обоснованной критикой возможности их осуществления на практике. Я постараюсь сделать это просто и понятно, руководствуясь мнением лауреата Нобелевской премии, одного из создателей атомной бомбы Э. Ферми:
«...В физике нет места для путаных мыслей, и физическая сущность любого действительно понимаемого вопроса может быть объяснена без помощи сложных формул».
Непонятое для немногих – буду пояснять в ответах на комментарии, для многих – в дополнительных постах.

Причины разработки СТО
Считается, что основная причина разработки СТО – кризис физики в конце Х1Х века. В 1855 – 873 гг. Максвеллом были предложены уравнения классической электродинамики, описывающие закономерности электромагнитных явлений в сплошной среде, эфире. Тогда считали, что свет является электромагнитными упругими волнами, которые распространяются в неподвижном эфире, заполняющем всё пространство. Если это так, то можно определить скорость движения Земли относительно эфира. Такой опыт проделали Майкельсон и Морли в 1887 г. Затем они и многократно другие учёные его повторяли. Для этого луч света разделяли на два и посылали эти лучи по направлению движения земли по орбите и поперёк неё, потом соединяли. Из-за сопротивления эфира скорость света вдоль движения земли должна быть меньше.  Но скорость света оказалась одинаковой в обоих направлениях. То есть сопротивления эфира не обнаружили. Но оно должно быть, раз эфир есть. Стали этому искать объяснение. Известные учёные (Лармор, Фитцджеральд, Лоренц, Пуанкаре) предположили, что причиной может быть сжатие движущихся тел от сопротивления эфира, компенсирующее уменьшение скорости света, а потом добавили и замедление времени. Они вывели формулы для уменьшения длины движущегося объекта и замедления времени от сопротивления эфира (формулы Лоренца) раньше Эйнштейна (рис.1).

Но это не разрешило проблемы наличия эфирной среды, так как свойства эфира должны быть противоречивы: он должен быть упругим как сталь для распространения различных волн без искажения, а сопротивление движению тел в нём = 0, но его сопротивление (по теории Лоренца и др.) сжимает электроны и большие тела при их движении. К тому же эфир в опытах Майкельсона и др. не был обнаружен. Всё это надо было объяснить. Но это был кризис не физики, а одной из её частей. И Эйнштейн его разрешил. Атомная физика в это время успешно развивалась: в 1896 г. А. Беккерель открыл радиоактивность урана; Мари и Пьер Кюри в 1898 г. – радий и полоний и т. д.

Как Эйнштейн расправился с эфиром и светом
Эйнштейн разрешил этот кризис тем, что он принял за основу теории следующие положения (постулаты):
1. Эфира нет, так как он не обнаружен в опытах.
2.  Скорость света в вакууме для всех тел, при их равномерном и прямолинейном движении – то есть в инерциальных системах отсчёта (ИСО) – постоянна и не зависит от движения источника и приёмника света.
3. Скорость света есть наибольшая скоростью движения. Но движение со скоростью света возможно только для света.
4. В различных инерциальных системах отсчёта движение описывается одинаковыми уравнениями, а законы природы действуют одинаково (принцип относительности).

На основе этих положений Эйнштейн в 1905 г. разработал механику, отличную от классической (Ньютоновской) – специальную теорию относительности (СТО), в которой время для движущегося объекта замедляется, длина уменьшается, масса с ростом скорости увеличивается. На какой основе и сколько времени Эйнштейн разрабатывал СТО? На этот вопрос мнения пишущих о нём различны: от безудержного восхваления до обвинений в плагиате. Сам Эйнштейн отмечал, что основным он считал ответ на вопрос, что можно увидеть, если двигаться за светом со скоростью света. Эйнштейн решил, что увидит свет. Поэтому он и принял пункты 2 и 3 (указанные выше) о скорости света.

Особенности СТО
Все выводы СТО следуют из постоянства скорости света и независимости её от движения источника и приёмника света. Что я и покажу в следующем посте. В природе все объекты движутся. Поэтому движение или неподвижность определяют относительно иных тел. Эйнштейн заключил, что можно считать, что поезд движется относительно неподвижной земли, а можно считать, что земля движется относительно неподвижного поезда. В СТО неподвижным считается тот объект, где находится наблюдатель (человек или приборы). Для движущегося объекта время замедляется, длина уменьшается тем быстрее, чем больше его скорость. Для земных скоростей эти изменения очень малы, но быстро растут при приближении скорости объекта к скорости света, то есть для космических объектов и скоростей. В таких случаях говорят о релятивистских скоростях и других параметрах движения. Замедление времени, уменьшение длины определяются в СТО по формулам Лоренца.

Почему восхищаются СТО?
Широкое распространение и восхищение специальной теорией относительности (СТО) вызвано тем, что она преподносится как эпохальный переворот в науке, полностью меняющий наше представление о связи пространства и времени, то есть о мироустройстве. Так ли это? Мы и выясним это в предлагаемых вниманию читателей серии постов.

Об общей теории относительности (ОТО)
Затем Эйнштейн разработал общую теорию относительности. В ней рассматривается движение с ускорением; но основное внимание уделяется теории гравитации (тяготения) с учётом искривления пространства и замедления времени вблизи массивных тел (солнца, земли и др.). В ОТО законы гравитации описываются тензорными уравнениями Эйнштейна.

Дополнение: Основные формулы Лоренца
В СТО все параметры движущегося тела обозначают штрихом ('): длина – L', время – t', масса – т' и т.д., а неподвижного – без штриха.Формулы Лоренца имеют простой вид:

В следующем посте по СТО будет рассмотрен основной парадокс СТО – замедление времени для движущегося объекта.

Темы следующих посты по СТО: Основной парадокс СТО – замедление времени для движущегося объекта. Различное толкование соотношения хода часов в публикациях по СТО. Относительность одновременности. Уменьшение длины предмета при движении. Парадокс близнецов. Связь пространства и времени. О пространстве Минковского. Трансцендентально-кинетическая теория времени М. С. Аксёнова. Получение эффектов СТО при отсутствии замедления времени. Об экспериментальных подтверждениях СТО и использовании её положений на практике.