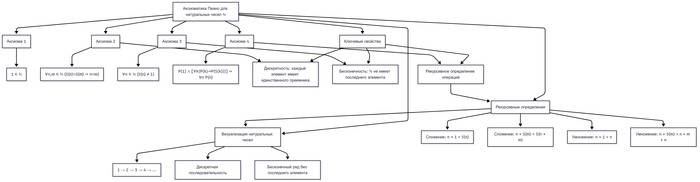
Аритмомахия (пункт 2, целые числа)
Мы прошли первую ступень этой иерархии, мир натуральных чисел (ℕ), идеальных для счета дискретных объектов. Но реальность богаче наших представлений о ней: она требует учета не только наличия, но и отсутствия, не только роста, но и убыли, не только движения вперед, но и направления назад. Натуральные числа с их ограниченностью a - b, где a > b, оказались недостаточными для описания всего спектра человеческого опыта и научных задач.
Продолжая наше путешествие по иерархии чисел ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ, мы вступаем в царство целых чисел (ℤ). Это мир, расширяющий горизонты ℕ, включая в себя не только положительные величины, но и их зеркальные отражения, отрицательные числа, а также важнейший символ пустоты и равновесия — ноль.
Примечание: ℕ, ℤ, ℚ, ℝ и ℂ— стандартные символы Юникода (exempli gratia, ℕ = U+2115), предназначенные специально для множества натуральных, целых, рациональных, вещественных и комплексных чисел соответственно. Использование данных символов исключает двусмысленность, вроде "...пусть N — натуральное число, тогда N ∈ N", что только запутает читателя.
Мир натуральных чисел (ℕ), мир счёта, сложения и умножения, казался древним математикам полным и самодостаточным. Однако сама жизнь ставила задачи, которые ℕ решить не могли:
Как выразить долг? Как формализовать убыль? Как решить уравнение x + 5 = 3?
Ответом стало появление целых чисел (ℤ), расширивших ℕ включением отрицательных чисел и нуля как полноценного объекта:
ℤ = {…, -3, -2, -1, 0, 1, 2, 3, …}.
Практические истоки целых чисел находятся в древних цивилизациях. В Китае эпохи Хань (200 г. до н.э.) трактат "Цзючжан Суаньшу" ввёл палочки двух цветов: красные для прибыли (正), чёрные для долга (負). Запись 赤三 黑五 (красные 3, чёрные 5) означала чистый долг в 2 единицы — прообраз -2.
В Индии V-VII вв. Брахмагупта в "Брахмаспхута-сиддханте" формализовал ноль и арифметику:
"...имущество" (дхана) + "долг" (рина) = их разность,
Произведение двух "долгов" (-a × -b) = "имущество" (+ab).
Хотя его попытка определить 0/0 = 0 была ошибочна, это смело расширило горизонты. Через исламский мир (аль-Хорезми, VIII-IX вв.) эти идеи достигли Европы, но встретили сопротивление.
Декарт в XVII веке называл отрицательные корни "ложными",
...но часто случается, что некоторые из этих корней ложны или меньше, чем ничто.
La Géométrie, 1637
а Паскаль отвергал вычитание 4 из 0 как абсурд:
...я понимаю, что можно обозначить долг знаком минус [...], но как можно представить величину меньшую, чем ничто?
Lettres de Pascal à Fermat, 1654
Современник Паскаля, английский математик Джон Валлис, парировал:
"...если кто-то не может понять, как -5 может быть меньше нуля, пусть представит термометр: температура ниже нуля действительно существует".
Перелом наступил лишь когда координатная прямая Декарта дала отрицательным числам геометрическую интерпретацию: точки левее нуля.
..и чтобы отличать эти равные, но противоположные по знаку числа, если корни истинные [положительные], я пишу их сразу после с знаком +; а если ложные [отрицательные], то с знаком -.
La Géométrie, 1637
Философский триумф целых чисел состоялся в XVIII-XIX веках. Леонард Эйлер в трудах по алгебре легитимировал операции с отрицательными числами,
Следовательно, ясно, что произведение -a на -b должно быть таким же, как произведение a на b, а именно +ab. ... Следовательно, если говорят, что -3 умножить на -4 дает +12, то это верное правило.)
Vollständige Anleitung zur Algebra, 1770
а Уильям Гамильтон включил ℤ в структуру коммутативного кольца (термин "коммутативное кольцо" появился позже, в 1897 у Д. Гильберта "Zahlbericht", формализован в 1921 Э. Нетёр "Idealtheorie in Ringbereichen" и устоялся в 1930 Б. ван дер Варденом "Moderne Algebra"), где каждое число имеет противоположное (a + (-a) = 0), а ноль стал нейтральным элементом (a + 0 = a, a × 0 = 0).
Ключевой скачок был не в символах, а в качественном преодолении ограничений ℕ:
1) Уравнение x + a = b разрешимо при любых a, b,
2) Появилась симметрия (-a как "зеркало" a),
3) Числа абстрагировались от контекста: -5 — не только долг, но и температура, смещение, заряд.
Как подчеркнул Герман Ганкель, это воплотило "принцип перманентности": законы ℕ сохранились при расширении до ℤ.
Если две формы, выраженные в общей арифметике, равны, то они должны оставаться равными и тогда, когда входящие в них символы перестают обозначать простые величины, и, следовательно, операции приобретают более общее содержание.
Законы арифметических операций, установленные для исходной системы чисел, должны сохраняться при любом их расширении, если только это не ведёт к противоречиям.
Объясним суть принципа на практике:
Возьмём сходный закон для ℕ, exempli gratia, дистрибутивность: a × (b + c) = a×b + a×c.
Расширение до ℤ:
При добавлении отрицательных чисел и нуля возник ключевой вопрос:
Как определить операции для новых объектов, чтобы старые правила не рухнули?
Пример с умножением:
Для натуральных 3 × 2 = 6.
Чтобы сохранить дистрибутивность в ℤ, пришлось принять:
3 × (-2) + 3 × 2 = 3 × ((-2) + 2) = 3 × 0 = 0 ⇒ 3 × (-2) + 6 = 0 ⇒ 3 × (-2) = -6
Так дистрибутивность потребовала положительное × отрицательное = отрицательное.
Принцип работает, только если новые объекты не создают парадоксов. Например, в ℤ сохранилось a × 0 = 0, но деление на ноль запрещено — оно разрушает структуру (1 = 2 и т.д.).
В прошлом посте мы обещали рассмотреть историю нуля подробнее. История нуля, напомним, началась с ранних форм-заполнителей пустоты (с 3000 г. до н.э.). Вавилоняне использовали двойной клин (˅˅) в шестидесятеричной системе (например, 1˅˅3 = 1×60² + 0×60 + 3), но это был лишь символ пропуска разряда, а не число.
Майя в I в. н.э. применяли знак-ракушку в двадцатеричном календаре для обозначения "начала" (день 0) и бесконечности, но не использовали его в вычислениях.
Древние Китай и Египет оставляли пустые места в записях (например, 4‿5 для 405), не создавая отдельного символа.
Революция произошла в Индии (III–IX вв.). В манускрипте Бакхшали (III–IV вв.) обнаружен древнейший символ нуля — жирная точка (●), служившая заполнителем в расчётах. Математик Брахмагупта в 628 г. в труде "Брахмаспхута-сиддханта" впервые определил ноль как число:
a + 0 = a, a − 0 = a,
a × 0 = 0,
0 ÷ a = 0 (деление на ноль он назвал "бесконечностью").
Символ превратился в кружок с именем "шунья" (санскр. "пустота"). Через арабов (Аль-Хорезми, IX в.) система распространилась в Европу: арабское "сыфр" (صفر) дало термины "цифра" и "шифр", а итальянцы преобразовали его в "zero".
В Европе (XII–XVII вв.) ноль встретил сопротивление.
В 1299 году Флоренция издала закон, полностью запретивший использование арабских цифр (включая ноль) в официальных документах, бухгалтерии и торговых записях. Арабские цифры легко поддавались исправлениям: например, 10 можно было превратить в 100 добавлением нуля, а 1 — в 7 или 9 минимальными правками. Власти требовали писать числа только словами или римскими цифрами, поскольку подделать текст было сложнее.
Церковь объявила его "дьявольским", ссылаясь на Аристотеля, отрицавшего пустоту. Однако купцы тайно использовали ноль в расчётах, а Фибоначчи в 1202 г. описал его в "Книге абака". К XV веку с развитием книгопечатания ноль узаконился. Научный прорыв совершил Декарт в XVII веке, сделав ноль началом координат в системе осей (x, y), что заложило основы аналитической геометрии и матанализа.
Хотя аксиомы Пеано описывают натуральные числа (ℕ), целые числа (ℤ) требуют более сложной структуры. Их можно построить двумя путями: расширением ℕ или независимой аксиоматизацией. Рассмотрим оба подхода.
1. Построение ℤ из ℕ через классы эквивалентности
Целые числа формально определяют как упорядоченные пары натуральных чисел (разность как абстракция):
(a, b) ∼ (c, d) ⇔ a + d = b + c.
Пример: (5, 3) ∼ (2, 0), так как 5 + 0 = 3 + 2 → обе пары кодируют число 2. Или (3, 5) ∼ (0, 2) → кодируют -2. Ноль: класс пар вида (a, a) (например, (4, 4) = 0).
Операции:
Сложение: (a,b) + (c,d) = (a+c, b+d),
Умножение: (a,b) × (c,d) = (ac+bd, ad+bc).
(5,3) (это 2) + (3,5) (это -2) = (8,8) = 0.
2. Аксиоматизация как коммутативного кольца
ℤ можно задать аксиомами алгебраической структуры (кольца). Основные аксиомы:
Сложение
1. Ассоциативность: ∀a,b,c ∈ ℤ: (a+b)+c = a+(b+c).
2. Коммутативность: ∀a,b ∈ ℤ: a+b = b+a.
3. Нейтральный элемент: ∃ 0 ∈ ℤ: ∀a ∈ ℤ: a+0 = a.
4. Обратный элемент: ∀a ∈ ℤ ∃ (-a) ∈ ℤ: a + (-a) = 0.
Умножение
1. Ассоциативность: ∀a,b,c ∈ ℤ: (a·b)·c = a·(b·c).
2. Коммутативность: ∀a,b ∈ ℤ: a·b = b·a.
3. Нейтральный элемент: ∃ 1 ∈ ℤ: ∀a ∈ ℤ: a·1 = a.
Дистрибутивность
∀a,b,c ∈ ℤ: a·(b+c) = a·b + a·c.
Отсутствие делителей нуля
a·b = 0 ⇒ a=0 ∨ b=0.
В ℤ есть симметрия (для каждого элемента существует противоположный), нет аксиомы индукции (она заменяется структурой кольца) и ℤ содержит ℕ как подмножество натуральных чисел (1, 2, 3, ...).
Отдельно отметим аксиомы порядка для ℤ
Чтобы ввести сравнение целых чисел, добавляют:
Трихотомия: ∀a,b ∈ ℤ верно ровно одно: a < b, a = b, a > b.
Монотонность сложения: a < b ⇒ a + c < b + c.
Монотонность умножения: a < b ∧ c > 0 ⇒ a·c < b·c.
-5 < 3, так как 3 - (-5) = 8 > 0.
Как ℕ вкладывается в ℤ?
Существует изоморфное вложение f: ℕ → ℤ, сохраняющее операции:
f(0_ℕ) = 0_ℤ,
f(S(n)) = f(n) + 1.
Так натуральные числа становятся подмножеством ℤ:
ℕ = {0, 1, 2, ...} ⊂ ℤ.
Введение целых чисел (ℤ) расширяет арифметику натуральных чисел (ℕ), но не преодолевает принципиальные ограничения, установленные теоремой Гёделя о неполноте. Рассмотрим причины.
Во-первых, почему ℤ не "сильнее" ℕ для теоремы Гёделя?
Целые числа строятся из натуральных через классы эквивалентности пар (например, (a, b) ∼ (c, d) ⇔ a + d = b + c). Любое утверждение о ℤ можно выразить в терминах ℕ. Если система аксиом для ℕ (Пеано) неполна, то её расширение до ℤ, основанное на тех же принципах, также будет неполным. Теорема Гёделя применима ко всем системам, содержащим арифметику ℕ.
Утверждение "...машина Тьюринга с номером n не останавливается на пустом вводе":
Формулируется через номера алгоритмов (n ∈ ℕ),
Остаётся недоказуемым в аксиомах Пеано и, следовательно, в ℤ, так как ℤ определяется через ℕ.
Во-вторых, однако, расширение до целых чисел решает конкретные алгебраические проблемы, но не затрагивает "неуловимость" гёделевских утверждений:
Разрешимость уравнений:
В ℤ всегда есть решение для x + a = b (где a, b ∈ ℤ), что невозможно в ℕ.
Недоказуемость мета-утверждений:
Гипотезы о свойствах ℕ (например, о распределении простых чисел) остаются за пределами формальных систем.
В-третьих, как и для натуральных чисел, так и для целых существуют принципиальные задачи или парадоксы, демонстрирующие сложность данной числовой системы.
1. Уравнение Пелля (x² - dy² = 1) и его фундаментальные решения
Для данного неквадратного целого d > 1, найти все целочисленные решения (x, y) уравнения x² - dy² = 1.
Пара (x, y) ищется именно в целых числах. Уравнение тривиально в ℝ, но его решения в ℤ обладают глубокой структурой.
Хотя известно, что существует бесконечно много решений (фундаментальное решение порождает их все алгоритмически), нахождение самого фундаментального решения для произвольного d не имеет известной эффективной формулы. Его "размер" (величина x и y) может быть астрономически огромным даже для умеренных d, что делает проблему вычислительно трудной. Задача упирается в тонкую арифметику колец целых алгебраических чисел, выходящую за рамки элементарной арифметики ℤ.
2. Проблема остановки для целочисленных линейных программ
Можно ли определить (алгоритмически или в рамках арифметики ℤ), остановится ли программа, которая на каждом шаге вычисляет значение линейного полинома с целыми коэффициентами от целочисленных переменных и проверяет условие вида P(x₁, x₂, ..., xₙ) >= 0 для перехода?
Переменные, коэффициенты, условия — все целочисленно. Это ограниченный, но важный класс программ, работающих исключительно с целыми числами и линейными операциями.
Проблема остановки даже для этого подкласса программ алгоритмически неразрешима. Это следствие неразрешимости общей 10-й проблемы Гильберта (доказанной Матиясевичем). Не существует алгоритма (и, следовательно, не может быть доказательства в достаточно сильной формальной системе, охватывающей ℤ), которое для любой такой программы и любого начального состояния целочисленных переменных корректно ответило бы, достигнет ли программа состояния остановки. Это конкретная неразрешимая проблема, живущая внутри ℤ.
3. Гипотеза Бёрча — Свиннертон-Дайер (BSD)
Гипотеза глубоко связывает алгебраические свойства (ранг) эллиптической кривой, заданной уравнением y² = x³ + ax + b с целыми коэффициентами a, b (и дискриминантом без квадратов), с аналитическими свойствами ее L-функции в точке s=1. Конкретно: порядок нуля L-функции в s=1 должен равняться рангу группы рациональных точек кривой.
Кривая определяется целыми коэффициентами. Ранг — это максимальное число независимых рациональных точек бесконечного порядка на кривой, но сама группа точек и ее структура неразрывно связаны с арифметикой ℤ и ℚ. Вычисление ранга — задача целочисленной арифметической геометрии.
Это одна из "Проблем тысячелетия". Доказательство (или опровержение) гипотезы BSD даже для кривых ранга 0 и 1 остается недостижимым. Она требует синтеза глубоких теорий (модулярные формы, L-функции, теория групп), выходящих далеко за рамки аксиоматики кольца целых чисел. Ее статус подчеркивает, что даже "естественные" вопросы о диофантовых уравнениях (частный случай — точки кривой с целыми/рациональными координатами) в ℤ могут быть невероятно сложными и, возможно, неразрешимыми в рамках "элементарных" систем.
4. Задача о представимости множеств полиномами над ℤ (проблема Диофанта , теорема Матиясевича):
Множество M ⊆ ℤ называется диофантовым, если существует полином P(x, y₁, y₂, ..., yₙ) с целыми коэффициентами такой, что: x ∈ M ⇔ ∃ y₁, y₂, ..., yₙ ∈ ℤ : P(x, y₁, y₂, ..., yₙ) = 0.
Вся задача — о существовании целочисленных решений полиномиальных уравнений для определения подмножеств целых чисел.
Теорема Матиясевича (решившая 10-ю проблему Гильберта негативно) показывает, что существуют алгоритмически неразрешимые множества целых чисел (например, множество номеров машин Тьюринга, останавливающихся на пустом вводе), которые тем не менее являются диофантовыми! Это означает, что для такого множества M существует полином P, как описано выше, но нет алгоритма (и не может быть доказательства в достаточно сильной формальной системе, основанной на ℤ), который по произвольному x ∈ ℤ корректно определил бы, принадлежит ли x множеству M. Это прямой пример гёделевской неполноты, воплощенный внутри арифметики целых чисел через диофантовы множества.
5. Проблема Фробениуса для n > 2 чисел:
Пусть даны n целых положительных чисел a₁, a₂, ..., aₙ, таких что НОД(a₁, a₂, ..., aₙ) = 1. Найти наибольшее целое число g(a₁, a₂, ..., aₙ), которое не может быть представлено в виде неотрицательной целой линейной комбинации: x₁a₁ + x₂a₂ + ... + xₙaₙ где xᵢ ∈ ℕ ∪ {0}.
Задача целиком о представлении целых неотрицательных чисел целочисленными комбинациями. Искомое число g — целое.
Для n=2 существует простая формула: g(a, b) = a·b - a - b. Однако для n >= 3 не существует общей замкнутой формулы для g(a₁, a₂, ..., aₙ). Более того, вычисление g для произвольного набора из n >= 3 чисел является NP-трудной задачей. Хотя это и не прямая недоказуемость в смысле Гёделя, это демонстрирует фундаментальную вычислительную сложность, присущую даже сравнительно простым комбинаторным задачам в ℤ. Невозможность найти общую эффективную формулу или алгоритм подчеркивает ограниченность наших возможностей предсказать поведение систем в ℤ.
Целые числа (ℤ) являются фундаментом цифровой эпохи: они лежат в основе криптографии (протоколы ZKP, zk-SNARKs), компьютерных систем (дополнительный код, координатные сетки) и точных наук (квантовые вычисления, инженерия).
Но даже ℤ недостаточно. Уравнение
2x = 1
неразрешимо в целых числах. Этот вызов приведёт нас к миру рациональных чисел (ℚ), следующей ступени великой иерархии ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ.
Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.