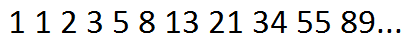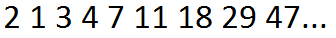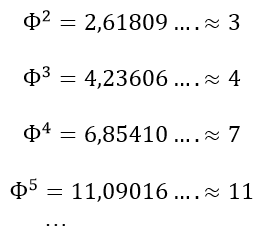Кошачье сечение
Показать полностью
1
0 просмотренных постов скрыто
Мелодия, золотое сечение, число Пи и 3,3333
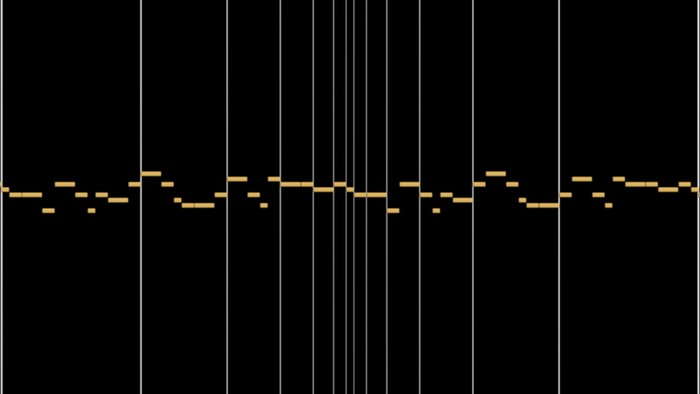
Мелодия имеет интересную особенность: если взять любую пару нот, то длительности этих нот будут между собой в пропорции золотого сечения (Ф=1,61803).
Длительности нот:
a = 1 секунда
b = a / Ф (0,618)
c = b / Ф (0,382)
Таких нот в мелодии 8, 12 и 4.
В сумме длительность мелодии 16,944 секунды.
Если сумму разделить на 4, то получим 4,236. Это золотое сечение в третьей степени. Любые 6 нот мелодии, звучащие друг за другом, в сумме равны Ф в кубе.
Мелодия цикличная, разрешается в первую ноту. Первая и последняя ноты соединяются в пропорции золотого сечения. Длительность мелодии плюс первая нота (a=1) в сумме равны 17,944. Это Ф в шестой степени.
Степени золотого сечения
Первые 2 ноты это Ф. Первые 3 ноты - Ф в квадрате. Первые 6 нот - Ф в кубе. Первые 9 нот - Ф в 4-й степени. Первые 15 нот - Ф в 5-й степени. Первые 25 нот (с учетом цикличности) - Ф в 6-й степени. Первые 41 нота (с учетом цикличности) - Ф в 7-й степени.
Возводить в степень можно и в обратном направлении. Первая и последняя ноты это Ф. Первая и последние 3 ноты – Ф в квадрате. Первая и последние 5 нот – Ф в кубе. Первая и последние 9 нот – Ф в 4-й степени. Первая и последние 15 нот – Ф в 5-й степени. Первая и последние 24 ноты – Ф в 6-й степени. Первая и последние 40 нот – Ф в 7-й степени.
Симметрия
Если взять вторую ноту любого такта, то длительности слева и справа от выбранной ноты будут симметричны друг другу. Тоже самое относится и к пятой ноте.
Если длительность второй ноты последовательно умножать на Ф, то полученные значения будут слева и справа, симметрично выбранной ноты. Точно также и пятая нота (показано на рисунке).
В мелодии есть еще один вид симметрии. Возьмём любую пару нот. Длительности нот, равноудаленные от этой пары, будут между собой в пропорции золотого сечения.
Золотое сечение, число Пи и 3,3333
Если длительность мелодии разделить на 3,3333, то получим 5,0832. Это произведение золотого сечения и числа Пи.
Ролик записан с частотой 30 кадров в секунду. Умножим длительность мелодии на 30 и получим 100 ФП.
Вариант №2
Если взять а = 0,618 (1/Ф) и всё пересчитать, то длительность мелодии составит 10,472 секунды. При делении на 4 будет Ф в квадрате. При делении на 3,3333 будет просто число Пи.
Показать полностью
1
1
Золотое сечение?
Слушайте, я один замечаю некоторую закономерность в распределении пропорций ингредиентов, когда готовлю еду?
Идеальный фруктовый салат: 1 банан и 2 мандаринки
Идеальная яичница: 1 сосиска и 2 яйца
Идеальный овощной салат: 1 огурец и 2 помидорки
Почему никто в кулинарии до сих пор не придумал "Правило Золотого Члена"?
Джонни Синс
Золотое Лысое сечение
Показать полностью
1
Тигр и 1,618
Ёшь твою клёшь! - подумал Штирлиц :)
Циркуль Фибоначчи или циркуль золотого сечения
Загорелся желанием сделать такой. Вроде всё что им поверено то и красиво.
Материал как нельзя кстати нашёлся, в прямом смысле, на дороге валялась железяка от пластикового окна. Фурнитура запирания и регулировок. Просто полоса оцинкованного железа. Медные трубки для заклёпок использовал от клапана Шрёдера, остались от ремонта холодильника. Ну в общем разметил, обточил и склепал. Всех работ на полчаса.
Но что это? Я меряю им те коробочки которые мне нравятся, но они не укладываются в золотое сечение. А сделал по указке циркуля, они не нравятся мне. Перепроверил размеры, всё вроде соответствует. Это что-то со мной не так, не вижу гармонии указанной Фибоначчи, или тут что-то другое?
Размеры из интернета Циркуля Золотого сечения
Медные трубки для заклёпок из клапана Шрёдера, резал трубкорезом на 2 мм длиннее чем толщина соединяемых деталей. После расклёпки они становятся вровень.
Вчера аварийно отключилось электричество, вот фото коробочек. Первые три в соответствии с золотым сечением, но мне больше нравится та которая на заднем плане. Хоть она и плоская, и пропорции у неё не попадают в размерность чисел Фибоначчи, но её приятно держать в руках, и зрительно она мне кажется более пропорциональной.
Показать полностью
4
Время прогревать аудиторию!
Сентябрь — это не только начало учебного года, но и время активной подготовки к горячему сезону распродаж. Самое время подключить подписку Пикабу+:
рассказывайте о своих товарах и услугах
добавляйте ссылки
создавайте витрину товаров прямо в профиле
подключайте дополнительное продвижение постов
Пора готовить сани!
Числа Люка
Данный пост не о хайповом не так давно люке в лесу, не о Люке Скайуокере и даже не о Люке Скайуокере в лесу.
Данный пост о последовательности чисел, которые называются "Числа Люка", и о их связи с так называемым Золотым сечением.
Многие наверняка уже слышали о числах Фибоначчи и их связи с Золотым сечением (если нет, это легко гуглится, или вот неплохая статья: тык).
Числа Фибоначчи, как известно, выглядят следующим образом:
Эдуард Люк подумал: а что если начать последовательность не с 1 и 1, а с 1 и 2. Однако если так сделать, то получится та же самая последовательность, но только без первой единицы. Тогда он решил поменять местами числа и начать последовательность не с 1 и 2, а с 2 и 1. Остальное все также: следующее число равно сумме двух предыдущих.
Таким образом последовательность чисел Люка выглядит так:
А теперь про связь с Золотым сечением.
Как известно, Золотое сечение Ф = 1.618033988749...
Всё, что мы будем делать, это возводить это число Ф в степень и округлять до ближайшего целого. И вот, что из этого получится:
Округленные числа совпадают с числами Люка. Таким образом мы из числа Ф получили последовательность чисел Люка. И у данных чисел связь с Золотым сечением выглядит даже сильнее, чем у тех же хайповых известных числах Фибоначчи.
Кто-то может сказать: "Всё это, конечно, здорово, последовательность получается. Но получается она посредством довольно грубого округления". На это можно ответить, что люди связывают математику с порой излишней точностью. Как будто если мы запишем миллион чисел после запятой, это будет только точнее отображать какое-то число. Но данный пример доказывает, что и при округлении можно получать замечательные результаты.
Показать полностью
1