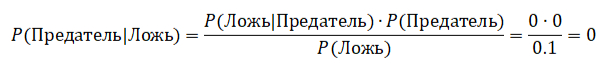UPD:
Парадокс B.Timethy — это феномен, при котором ложная аксиома, принятая в качестве основы в какой-либо системе, вызывает последовательность взаимно усиливающих ошибок и искажённых интерпретаций, приводящих систему к регрессивному развитию, замкнутому кругу или полному распаду.
Ключевые характеристики
Принимаемая ложная аксиома.
Изначально в систему вводится неверное утверждение, принимаемое всеми участниками за абсолютную истину. Оно становится базой для дальнейшей деятельности и правил поведения.
Интерпретация действий.
Все последующие шаги и реакции членов системы определяются исходя из начальной ложной аксиомы. Часто такие действия носят защитный или контрпродуктивный характер.
Система самоподтверждающихся заблуждений.
Выводы, полученные из ложной аксиомы, поддерживают и подтверждают друг друга, создавая иллюзию устойчивости и обоснованности системы, несмотря на внутренние противоречия и абсурдность.
Снижение надёжности и продуктивности.
Накопленные ошибки негативно сказываются на работе системы, уменьшая её эффективность, замедляя темпы прогресса и ухудшая координацию взаимодействия участников.
Недостаточная саморефлексия.
Несмотря на наличие очевидных недостатков и результатов, противоречащих начальным утверждениям, участники могут продолжать следовать прежним правилам, оказывая сопротивление любым попыткам ревизии базовых понятий.
Возможность радикальных изменений.
Внешний фактор или появление убедительных доводов, опровергающих главную аксиому, способно вызвать кардинальные изменения в состоянии системы: развал старых догм и начало нового этапа развития.
Риск регресса или коллапса.
Если система не способна адекватно реагировать на новые обстоятельства, она рискует потерять свою функциональную ценность, начать стагнировать или прекратиться окончательно.
Давайте представим простую ситуацию, где 25 человек собрались в виртуальной комнате за столом, чтобы найти предателя. Им говорят: «Среди вас три предателя, которые будут лгать и делать все что бы их не нашли. Ваша задача — вычислить их, иначе все проиграете». Участники кивают, готовые к рациональному поиску. Но есть нюанс: предателей нет. Все 25 — честные игроки, верящие в условность угрозы.
Сначала группа действует логично:
— Кто предложил странный алгоритм? Возможно, это предатель!
— Почему Никола молчит? Наверное, скрывает свою роль!
Каждое действие, каждое слово теперь воспринимается через призму подозрений. Даже те, кто пытается доказать свою невиновность, попадают в ловушку:
— «Я точно мирный!» → «Слишком настойчиво отрицаешь — значит, врешь!»
— «Давайте проверим все версии» → «Ты тянешь время, чтобы саботировать нас!»
Через час комната превращается в поле боя. Участники голосуют за исключение «предателей», но их список всё растёт. Когда остаётся 10 человек, кто-то задаёт роковой вопрос: «А если предателей и не было?..» Но уже поздно — группа развалилась, предатель не найден, а доверие уничтожено.
Это и есть парадокс B.Timethy: ложная аксиома о несуществующей угрозе запускает механизм самоуничтожения даже среди рациональных людей. Система, где каждый уверен лишь в собственной невиновности, обречена искать врагов, которых нет… пока не исчезнет сама.
«Одна ложная аксиома, брошенная в тишину, рождает эхо тысячи вопросов. Но ответы, как тени в зеркальном лабиринте, всегда указывают на тех, кто их ищет. Так рождается парадокс B.Timethy — мир, где невидимые враги сильнее любых фактов, а доверие становится жертвой собственной бдительности» - B.Timethy
Парадокс B.Timethy в жизни человека
Парадокс B.Timethy — это феномен, заключающийся в том, что введение ложной аксиомы в систему приводит к возникновению серии самоусиливающихся подозрений и конфликтов, в результате чего система приходит либо к полному краху, либо к бесконечной спирали взаимных обвинений и подозрений.
В систему внедряется утверждение-триггер (например, «Среди нас есть предатель»), которое принимается как истина без доказательств.
Рациональные действия участников, основанные на ложной аксиоме, генерируют новые «доказательства» угрозы, усиливая паранойю.
Система не может самостоятельно опровергнуть ложь из-за замкнутости и отсутствия нейтрального арбитра.
Число взаимных обвинений будет расти с каждым разом.
• 1 — абсолютная вера в ложную аксиому.
• 0 — полная разобщённость,
• 1 — идеальная командная работа.
• 0 — система не может проверить информацию,
• 1 — мгновенная верификация лжи.
P ≥ 1 ⇒ Система разрушается.
При L=1, S=0, R=0 → P → ∞ (крах)
При L=0 → P=0 (стабильность)
От сотрудничества к хаосу: Как ложь за общим столом губит любую систему
Ранее (в самом начале статьи) вы уже ознакомились с примером, так называемым «Зеркальный стол B.Timethy», где есть только две версии:
1. Всё сводится к разрушению системы.
2. Всё сводится к бесконечным подозрениям.
Если быть точнее, то в первой версии мы даем людям управлять системой(исключать подозреваемых), что и приведет к разрушению системы, а во второй версии мы не дадим управлять системой, то есть исключать людей и агентам нужно будет понять кто предатель по любым факторам(речь, движения и т.д.), но нюанс: предателей нет и никто из агентов не знает, что их нету, что и сводиться к бесконечным подозрениям(→ ∞), но это не единственный пример и версии которыми можно продемонстрировать парадокс B.Timethy.
Примеров может быть много, но суть парадокса остается одна "Неизвестность", а дальше либо разрушение системы либо тупик в виде бесконечности.
Человек N даёт интервью, где лжёт: «Самое неприятное, что я слышал — угрозы от одного из моих друзей». У N есть 25 друзей, которые не знакомы друг с другом. Все они смотрят интервью и начинают рассуждать:
Друг А: «Это не я → значит, кто-то из остальных 24».
Друг Б: «Я точно не виновен → значит, виноват другой».
... И так все 25.
Ложная аксиома: Угроза существует, но источник неизвестен.
Цикл подозрений:
Каждый друг исключает себя из списка («я знаю, что не я»), но не может исключить остальных.
Возникает иллюзия «врага» среди незнакомцев, что порождает абстрактный страх.
Ложная аксиома → Страх → Поиск «доказательств» → Новые подозрения → Усиление страха
Что и порождает бесконечный цикл подозрений.
Таким образом можно продемонстрировать "Парадокс B.Timethy", предлагаю на примере "Зеркального стола B.Timethy" разобраться в следующем...
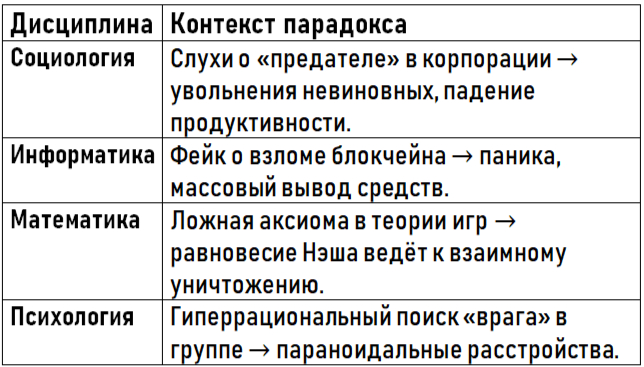
Парадокс B.Timethy: Междисциплинарный анализ и возникающие сомнения
Парадокс B.Timethy, где ложь о несуществующей угрозе запускает бесконечный цикл подозрений, бросает вызов основам множества научных дисциплин. Вот как он ставит под сомнение ключевые концепции в каждой из них:
1. Математика: Кризис формальной логики и теории игр
В математике парадокс B.Timethy порождает много разногласий ведь даже в системе с рациональными агентами, следующими строгим правилам, ложь порождает неразрешимые противоречия.
Классические модели равновесия (Нэша, Штакельберга) предполагают, что агенты действуют в условиях полной информации. Парадокс B.Timethy показывает, что асимметрия информации превращает рациональные стратегии в инструмент саморазрушения.Пример: Если все игроки выбирают «подозревать», система достигает псевдоравновесия, где выигрыш для всех равен нулю.
Формула Байеса для обновления вероятностей терпит крах, когда ложь встроена в систему как аксиома.
но группа игнорирует этот результат, продолжая поиск.
Вывод: Математика не может разрешить парадокс, не изменив исходные аксиомы системы, что ставит под вопрос универсальность формальных моделей.
2. Социология: Крах теории рационального выбора
В социологии суть парадокса B.Timethy заключается в коллективном недоверие, возникающее даже в группах, где участники действуют логично и добросовестно.
Модели, предсказывающие устойчивость сетей (например, теория «сильных и слабых связей»), не учитывают, что одна ложь может разорвать даже самые прочные связи.
Доверие, считавшееся основой общества, оказывается его ахиллесовой пятой. парадокс B.Timethy доказывает, что социальный капитал может быть отрицательным, если система заражена дезинформацией.
Вывод: Социология больше не может игнорировать «темную сторону» рациональности — алгоритмы взаимодействия, ведущие к самоуничтожению.
3. Информатика: Провал децентрализованных систем
Децентрализованные сети, созданные для устойчивости к обману, оказываются уязвимы к парадоксу B.Timethy.
Даже прозрачная запись транзакций не спасает от паники, если ложь о «взломе» становится общепринятой.
Пример: В 2022 году фейк о уязвимости в Ethereum вызвал обвал курса на 30% (CoinDesk, 2022), хотя код был безопасен.
Алгоритмы, обученные выявлять фейки, сами становятся инструментом парадокса, если группа им не доверяет.Пример: Модель GPT-4, опровергающая ложь, была обвинена в «предвзятости», что усилило подозрения.
Вывод: Децентрализация и алгоритмы не защищают от B.Timethy — нужны принципиально новые протоколы, включающие «иммунитет к панике».
4. Философия: Конец объективной истины
Из определения парадокса B.Timethy можно выявить, что истина перестает быть общей категорией, превращаясь в субъективное убеждение.
Парадокс реанимирует скептицизм Пиррона: «Если система не может отличить правду от лжи, можно ли вообще что-то знать?»
Высказывание «Предатель существует» становится перформативным — оно создает реальность, а не описывает её. Это бросает вызов теории речевых актов Остина.
Даже если ложь раскрыта, группа не может вернуться к исходному состоянию доверия. Это ставит под вопрос идею морального прогресса.
Вывод: Философия вынуждена признать, что истина — не абсолют, а функция доверия к системе.
5. Психология: Рациональность как патология
Так же парадокс может иметь характер когнитивного искажения, усиленные логикой, приводят к иррациональным решениям.
Участники не испытывают диссонанса, даже когда их подозрения опровергнуты — вместо этого они изобретают новые конспирологические объяснения.
Чем меньше группа знает о реальной угрозе, тем увереннее она в своих ложных выводах.
Вывод: Рациональное мышление не спасает от иррациональности — оно становится её инструментом.
6. Физика: Термодинамика социальных систем
Парадокс B.Timethy можно описать как метафору социальной энтропии — условную меру хаоса, возникающего из порядка. Это не прямое применение законов термодинамики, а аналогия для иллюстрации распада систем.
Если считать доверие аналогом «порядка», а подозрения — «хаоса», парадокс нарушает закон: система генерирует энтропию без внешнего воздействия.
Участники находятся в «суперпозиции» виновности, пока группа не проведет «измерение» (обвинение), но каждое измерение влияет на систему.
Вывод: Физические законы, кажется, не работают в социальных системах и других дисциплинарных науках, что требует новых междисциплинарных моделей.
Но не все так плохо парадокс B.Timethy показывает какие проблемы возникают при "Ложных аксиом" внедренные в систему, так же парадокс может помочь в разных науках и дисциплинах, а не только усугубить их.
Польза парадокса B.Timethy в науках и дисциплинах
Польза парадокса B.Timethy в науках и дисциплинах заключается в том, что он выступает как «диагностический инструмент», выявляющий скрытые уязвимости систем, а также стимулирует развитие новых теорий и подходов. Вот как его изучение обогащает различные дисциплины:
1. Математика и теория игр
Парадокс обнажает ограничения классических моделей (равновесие Нэша, теория вероятностей) в условиях асимметрии информации.
Создание новых моделей с учётом дезинформации как игрового фактора.
Разработка алгоритмов для систем, где участники не доверяют друг другу, но вынуждены сотрудничать (например, криптографические протоколы).
Учёт иррационального поведения в формальных уравнениях.
2. Социология и политология
Парадокс объясняет, как ложные аксиомы разрушают социальный капитал, и показывает, что рациональность ≠ устойчивость.
Выявление триггеров распада сообществ (от корпораций до государств).
Разработка методов профилактики паники в кризисных ситуациях.
Понимание, как децентрализованные системы могут избежать коллапса через механизмы «анти-Тimethy» (например, открытые источники информации).
3. Информатика и кибербезопасность
Парадокс демонстрирует уязвимость децентрализованных систем к мнимым угрозам.
Создание алгоритмов, устойчивых к информационным атакам (например, блокчейн с проверкой слухов).
Разработка ИИ-моделей, способных отличать рациональные подозрения от параноидальных.
Улучшение систем модерации для борьбы с самоусиливающейся дезинформацией.
4. Философия и эпистемология
Парадокс ставит под сомнение объективность истины и роль доверия в её формировании.
Переосмысление понятий «факт» и «консенсус» в эпоху фейков.
Развитие этических моделей, где ложь рассматривается как системная угроза.
Исследование, как язык создаёт реальность (перформативная функция высказываний).
5. Психология и когнитивистика
Парадокс показывает, как рациональное мышление усиливает иррациональные страхи.
Изучение когнитивных искажений, связанных с доверием (например, «эффект слепой рациональности»).
Разработка методов деэскалации паранойи в группах.
Тренинги для лидеров по управлению коллективной тревожностью.
6. Физика и теория сложных систем
Парадокс предлагает метафору «социальной энтропии» — меры хаоса, возникающего из порядка.
Моделирование систем, где "доверие" выступает аналогом энергии.
Применение принципов термодинамики к анализу устойчивости сетей (социальных, экономических, цифровых).
Парадокс B.Timethy объясняет, как слухи обрушивают рынки, даже если угрозы нет.
Создание механизмов быстрой верификации информации (например, алгоритмы для отслеживания фейков).
Разработка регуляторных мер против панических атак на рынки.
Главная междисциплинарная польза:
Парадокс B.Timethy объединяет науки, показывая, что ключевые проблемы современности (дезинформация, распад доверия, кризисы управления, ложные аксиомы) требуют комплексного подхода. Он:
Стимулирует диалог между математиками, социологами и программистами.
Показывает, что «рациональные» системы могут быть хрупкими, если игнорируют человеческий фактор.
Даёт язык для описания коллапсов — от соцсетей до политических режимов.
И тому подобное, где может пригодится парадокс.
(За счет "Ложной аксиомы" парадокс применим не только к обществу, но и к другим областям науки.)
Заключение: Парадокс B.Timethy — зеркало хрупкости человеческих систем
Парадокс B.Timethy — это не просто теоретическая головоломка, а мощная метафора, раскрывающая уязвимость любых систем, построенных на доверии. Его суть в том, что ложь или дезинформация, принятая как аксиома, запускает цепную реакцию саморазрушения. Даже рациональные действия участников, направленные на «спасение», лишь усугубляют хаос, превращая сотрудничество в войну всех против всех.Из всего этого можно сделать вывод что:
Одного вымышленного утверждения («Среди нас предатель») достаточно, чтобы разорвать социальные связи. Система начинает «пожирать» саму себя, генерируя мнимые доказательства угрозы.
Попытки логически вычислить несуществующего врага лишь усиливают паранойю. Разум, лишённый опоры на объективную истину, становится инструментом самоуничтожения.
Парадокс вскрывает кризисы в математике, социологии, ИИ и философии, показывая, что даже продвинутые модели не защищены от коллапса, если игнорируют человеческий фактор — страх перед неопределённостью.
Парадокс B.Timethy учит нас:
Проектировать системы с «иммунитетом» к ложным аксиомам (например, алгоритмы проверки слухов в соцсетях).
Ценить доверие как хрупкий ресурс, который нельзя восстановить через поиск виноватых.
Принимать неопределённость как данность, а не как угрозу.
Человечество стоит перед выбором: продолжать искать врагов в зеркалах собственных страхов или сделать шаг назад — и увидеть, что главная угроза кроется в нашей готовности верить в её неизбежность. Парадокс B.Timethy — не приговор, а призыв к смирению перед сложностью мира, где даже рациональность требует мудрости.
Эта статья относиться больше к философии нежели чем к строгому научному доказательству!
Автор парадокса: Timofey Belikov(B.Timethy)