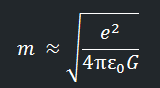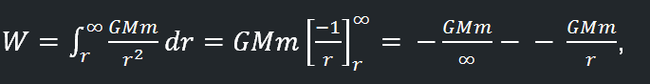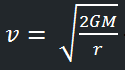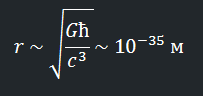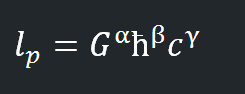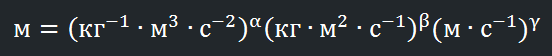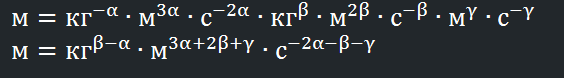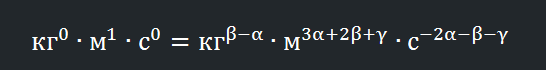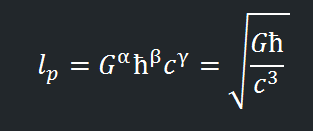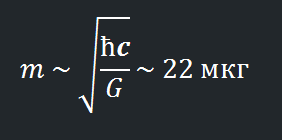Естественные единицы измерения и воксельная вселенная
Предупреждение: данный пост содержит некоторое количество формул, однако, они вполне доступны для понимания даже школьнику, ничего сложного, обещаю!
Аршин, локоть, спан, ярд, фут, лига, метр, километр – за время своего существования люди придумали огромное количество единиц измерения (в частности –длины), каждая из которых была вполне естественной для современников, которые их использовали. Во времена, предшествовавшие промышленной революции, однако, у людей возникла необходимость в некоей стандартизации единиц измерения. Благодаря усилиям множества людей, сейчас, спустя почти 300 лет, мы имеем международную систему СИ, в которой единицы длины, массы, времени и прочих физических характеристик точно определены и привязаны к естественным природным константам. Осталось лишь несколько стран, не использующих в быту метрическую систему. Самая известная из них – США. Отдельные американцы даже находят в этом повод для некоей гордости, однако, мало кто из них знает, что американская система стандартов уже давно определяет значения ярда, фунта и прочих величин через переводные коэффициенты с единиц измерения СИ.
Система единиц измерения, используемая нами в повседневной жизни, вполне нас устраивает. Мы все имеем прекрасное представление о метре, килограмме, секунде. Тем не менее, людям, которые занимаются научными изысканиями, этого мало, так как зачастую они исследуют объекты либо слишком огромные, такие как галактики, либо слишком малые – такие как атомы. Действительно, хотя мы и можем выразить размеры любого объекта через метры, используя приставки, мы уже с трудом понимаем, чем, например, пикометр отличается от аттометра. Подавляющее большинство из нас даже не сможет сказать, что больше, а многие – вообще не слышали о таких приставках.
В 1899 году немецкий физик Макс Планк раздумывал, наверное, над чем-то подобным, потому и написал следующее:
Все до сих пор используемые системы единиц, в том числе так называемая абсолютная СГС-система, обязаны своим происхождением пока что случайному стечению обстоятельств, поскольку выбор единиц, лежащих в основе каждой системы, сделан не исходя из общей точки зрения, обязательно приемлемой для всех мест и времён, но исключительно исходя из потребностей нашей земной культуры…
Результатом его раздумий явилась работа, опубликованная в 1900 году, в которой он предложил систему единиц измерения…
…которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений».
Макс Планк - герой этого поста
Забегая вперёд, скажу, что данный труд впоследствии был использован в большей части теоретической физики, а большинство общепринятых в настоящее время единиц измерения выведены напрямую из системы измерений, названных в его честь: Планковскими единицами.
До чего же он додумался? Предлагаю вместе пройти по пути его рассуждений.
Представим, что у нас есть пара электронов на расстоянии r друг от друга:
Что будет происходить, если бы мы начали сводить эту пару электронов всё ближе и ближе друг к другу?
1. Поскольку электроны обладают массой, между ними будет иметь место сила гравитационного притяжения, стремящаяся их сблизить.
2. Так же, мы знаем, что электроны имеют отрицательный электрический заряд, поэтому между ними будет иметь место электростатическая сила, расталкивающая их друг от друга.
Какая же из двух сил будет сильнее по мере их сближения (когда r → 0)? По закону всемирного тяготения, сила притяжения между двумя электронами будет выражена формулой:
Fg = G m₁ m₂ / r² – сила прямо пропорциональна произведению масс электронов и обратно пропорциональна квадрату расстояния между ними. В нашем эксперименте, m₁ и m₂ одинаковы и равны массе электрона, которую можно просто обозначить m, и переписать уравнение так:
Fg = G m² / r²
Сила электростатического расталкивания определяется по закону Кулона по такой формуле:
Fe = Q₁Q₂ / 4 πε₀ r² – эта сила прямо пропорциональна произведению двух зарядов и так же – обратно пропорциональна квадрату расстояния между ними. В данном случае, коэффициент пропорциональности задаётся ε₀ - электрическая постоянная (электрическая проницаемость вакуума). В нашем примере обе величины Q₁ и Q₂ равны e – заряду электрона, поэтому, формулу можно переписать так:
Fe = e² / 4 πε₀ r²
Посмотрим на отношение сил, чтобы понять, какая из них будет преобладать Fe / Fg = ? Запишем отношение:
Fe / Fg = e² / 4 πε₀ Gm²
Первое, что можно заметить, что r² сократилось, а это значит, что отношение двух сил никак не зависит от расстояния между двумя электронами и всегда будет одним и тем же (Хаха, нет! Но об этом позже). Зная значения всех элементов данного уравнения, подставив их и произведя расчёты, мы получим:
Fe / Fg = e² / 4 πε₀ Gm² ≈ 10⁴²
Иными словами, сила электростатического расталкивания превышает силу гравитации на 42 порядка! Чтобы полнее ощутить масштабы, запишу так:
Fe ≈ 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 * Fg.
Во столько раз гравитация слабее электромагнетизма, но именно гравитация была обнаружена первой. Почему? Потому что атомы, из которых состоит вещество, электрически нейтральны, положительный заряд протонов компенсируется отрицательным зарядом электронов. Из-за нейтральности атомов мы просто не замечали исключительно сильное электромагнитное взаимодействие. Гравитация – другое дело. Насколько можно судить сейчас, такой штуки как «отрицательная масса» не существует (во всяком случае, до сих пор никому не удалось обнаружить ничего похожего), поэтому два тела, обладающих массой, будут всегда испытывать взаимное притяжение.
Упрощённая Ньютоновская модель позволила нам сделать вывод о том, что отношение сил электростатического расталкивания и гравитации вообще не зависят от расстояния между двумя электронами, но, к сожалению, реальный мир не всегда так прост, как наши математические модели. Как обычно, её величество квантовая механика всё портит.
Чем меньше становится расстояние между электронами тем сильнее проявляется роль принципа неопределённости Гейзенберга (подробнее можно почитать в этом моём посте) – чем точнее мы пытаемся определить положение электронов в пространстве, тем сильнее разброс в их импульсах, тем больше они «дрожат», а чем сильнее эта «дрожь», тем выше их энергия. В какой-то момент, эта энергия становится достаточной для того, чтобы создать новый электрон (принцип эквивалентности массы и энергии А. Эйнштейна, знаменитое уравнение E = mc²). На самом деле мы можем легко посчитать расстояние между электронами, при котором наступят подобные условия, скомбинировав уравнение Эйнштейна с неравенством принципа неопределённости Гейзенберга.
Запишем уравнение таким образом: если мы ограничиваем объект в определённой области пространства размера ∆x, неопределённость в импульсе такого объекта ∆p должна быть примерно больше ħ / ∆x:
∆p ≳ ħ / ∆x
(ħ – редуцированная Планковская константа – просто коэффициент преобразования между энергией фотона и его частотой. На данном этапе достаточно понимать, что это константа).
В нашем случае с двумя электронами ∆x = r – расстояние между ними (∆p ≳ ħ / r).
Если импульс объекта растёт, очевидно, что растёт и энергия данного объекта, поэтому мы можем выразить энергию в данном выражении, умножив обе части на скорость света (с):
∆E ≳ ħ c / r
Кто сомневается, может вспомнить, что импульс – это произведение массы на скорость, а произведение единиц импульса (кг•м/с) на скорость (м/с) даст вам выражение единицы энергии (Джоуля) по определению (1 Дж = 1 Н•м=1 кг•м²/с²).
Из этого соотношения мы видим, что при уменьшении r, ∆E будет увеличиваться. Эта как раз энергия той квантовомеханической «вибрации», которую мы упускали из виду, используя уравнения классической механики. Теперь, имея на руках это соотношение, мы можем «прикинуть», какому расстоянию между электронами будет соответствовать энергия, достаточная для создания массы электрона по уравнению Эйнштейна (∆E ~ mc²), где m – масса электрона. Иными словами, нам нужен ответ на вопрос, когда соблюдётся отношение:
r ≲ ħ / mc
Подставив известные значения констант и массы электрона, мы получим:
ħ / mc ≈ 10⁻¹³ м
Это расстояние меньше среднего размера атома, которое составляет примерно 10⁻¹⁰ м, но сильно больше размера ядерного ядра (10⁻¹⁵ м). Иными словами, полученная величина говорит нам о том, что если мы попытаемся сблизить два электрона на расстояние, меньшее 10⁻¹³ м, квантовая неопределённость в их энергии будет достаточной для создания нового электрона. То есть, на этом расстоянии уже нельзя пренебрегать ни квантовой механикой, ни теорией относительности.
Но что будет, если мы будем продолжать сближать электроны друг к другу? Мы уже убедились, что согласно Гейзенбергу, с уменьшением расстояния ∆x растёт энергия ∆E, а согласно Эйнштейну, это эквивалентно добавлению массы в нашу систему. А раз гравитация у нас взаимодействует с массой, то расти будет и Fg (гравитационное притяжение между электронами)? С ростом массы, соотношение сил электростатического расталкивания и гравитационного притяжения уже не будет оставаться неизменной величиной, посчитанной нами ранее (10⁴²).
И так, следующий вопрос, на который нам надо найти ответ – при какой расстоянии между электронами гравитационное притяжение станет сравнимым с электростатическими силами, расталкивающими заряды по закону Кулона?
Для этого, мы просто должны выяснить, при каком значении m, выполнится данное условие:
Fe / Fg = e² / 4 πε₀ Gm² ≈ 1
Преобразуем уравнение к следующему виду:
Теперь, это значение массы можно преобразовать к энергии и подставить в выражение принципа неопределённости. После всех преобразований, получим:
r ≲ ħ / mc ≈ 10⁻³⁴ м
На этом расстоянии, гравитационное притяжение между электронами уравновесит силу их электростатического расталкивания, но что произойдёт, если мы продолжим уменьшать расстояние между электронами? Разумеется, гравитационное взаимодействие будет только увеличиваться, но будет ли это продолжаться всегда?
Оказывается, что нет. В дело снова вступит теория относительности и предъявит свой самый эффектный козырь – чёрную дыру. Здесь нужно чуть отвлечься от наших электронов и разобраться, какие условия вообще способствуют образованию чёрной дыры.
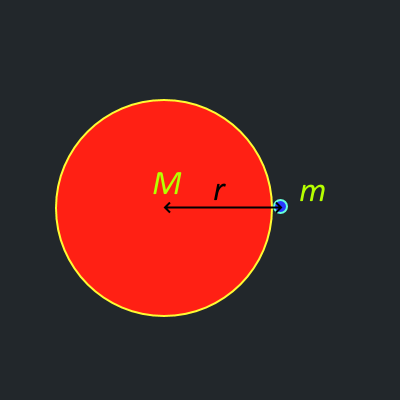
Давайте рассмотрим тело с малой массой m, расположенное на поверхности большего тела с массой M.
Между этими двумя телами действует сила гравитационного притяжения, выраженная формулой:
F = G Mm / r²,
… и, чтобы оторвать малое тело от поверхности большого, мне необходимо совершить работу по преодолению этой силы. Если я удалю малое тело от большого на некоторое расстояние dr, я совершу работу:
dW = F dr = (GMm / r² ) dr
Но если мне потребуется понять, какую работу мне необходимо совершить, чтобы удалить малое тело на бесконечно большое расстояние, так как сила притяжения между двумя телами будет убывать обратно пропорционально квадрату расстояния между этими двумя телами – надо будет проинтегрировать:
чтобы убедиться, что полная работа будет равняться:
W = GMm / r
По мере удаления m от M, тело будет набирать потенциальную энергию, и полная величина этой потенциальной энергии будет равняться полной проделанной работе.
Вооружившись этим знанием, я могу задаться вопросом, с какой скоростью мне надо подбросить m, чтобы оно вырвалось из области гравитационного притяжения M. Или, если перефразировать: какую скорость надо придать m, чтобы оно смогло удалиться на произвольно большое (бесконечное) расстояние от M?
Поскольку я только что посчитал, какая энергия необходима для этого, мне достаточно сообщить m такую же кинетическую энергию. Зная формулу кинетической энергии, получаю:
½ mv² = GMm/r
Решаем уравнение в отношении v (скорости) и получаем:
в русскоязычной терминологии эта скорость получила название «Вторая космическая скорость» (скорость освобождения или скорость убегания). Для Земли эта скорость составляет приблизительно 11 км / с, а, например, для Юпитера – уже около 60 км / с.
Из формулы видно, что вторую космическую скорость определяют два фактора – масса тела и его радиус – большая скорость освобождения требуется не только при старте с массивного объекта, но и с более плотного (чем в меньший объём «упакована» масса, тем сложнее с неё улететь).
И следующий вопрос, которым может озадачиться пытливый ум – а что случится, если объект будет настолько плотным, что вторая космическая скорость для него сравняется со скоростью света? Такие объекты получили название «чёрная дыра», так как даже свет не может покинуть их окрестности. Уже зная формулу, мы можем просто подставить в уравнение скорость света и решить его для любой массы (плотности), а преобразовав его для r – получим уравнение радиуса, внутрь которого необходимо «упаковать» массу M, чтобы образовалась чёрная дыра:
Rs = 2GM / c²
Эту величину называют «Радиусом Шварцшильда», в честь немецкого физика Карла Шварцшильда, который впервые решил уравнения Эйнштейна для такого случая и, тем самым, предсказал существование чёрных дыр.
Так какое отношение это всё имеет к нашим электронам? Самое непосредственное. Мы уменьшаем расстояние между ними, масса системы растёт, а размеры уменьшаются. Рано или поздно мы «упакуем» их достаточно плотно, так, чтобы в этой области пространства сформировалась чёрная дыра. А, имея необходимые формулы, мы можем вычислить, когда это произойдёт.
Во-первых, мы можем оценить, сколько гравитационной массы содержится в системе из двух электронов на расстоянии r друг от друга (r ~ ħ / mc). И так же, мы только что посчитали, как радиус Шварцшильда связан с гравитационной массой (r ~ Gm/c²). Объединив эти два уравнения, мы увидим, что m сократится, а всё, что останется можно записать следующим образом:
Что примечательно, если внимательно приглядеться к этой формуле, можно заметить, что она целиком состоит из констант и никак не содержит никаких других параметров. Мы можем взять не только электроны, но и любые иные два объекта, и если мы уменьшим расстояние между ними до 10⁻³⁵ м, в данном объёме неизбежно возникнет чёрная дыра и на этом этапе мы больше не сможем извлечь никакой дополнительной информации из системы. Даже если вы захотите «вкачать» в систему ещё больше энергии, это приведёт лишь к росту этой чёрной дыры.
Мы подошли к фундаментальному пределу, точнее которого мы физически не в состоянии ничего измерить. Данный предел, по фамилии его первооткрывателя носит название Планковская длина. Это граница, где заканчиваются даже наши теоретические возможности познания пространства. Примечательно, что на данном пределе и квантовая механика и теория относительности становятся одинаково важны.
Тут человек, знающий историю научных открытий, может спросить – но ведь Планк опубликовал свои труды раньше, чем Эйнштейн опубликовал свою теорию относительности, да и до открытия принципа неопределённости было ещё далеко!
Поэтому сейчас мы пройдём по пути, пусть менее наглядному, но доступному Максу Планку в самом конце 19 века.
В наших выкладках можно увидеть постоянное использование 3 разных констант из трёх областей физики. Мы использовали постоянную Планка-Дирака (E = ħω) , основную константу квантовой механики; так же – скорость света (E = mc²), основную константу общей и специальной теории относительности, а так же Ньютоновскую универсальную гравитационную константу (F = G (m1m2 / r²). Здесь можно задаться вопросом – каковы фундаментальные, базовые единицы измерения для этих трёх констант?
Все возможные единицы измерения являются производными от 7 базовых:
Расстояние – метр, м
Время – секунда, с
Масса – килограмм, кг
Электрический ток – Ампер, А
Количество вещества – моль
Интенсивность света – канделла, Кд
Температура – кельвин, К
(четыре последних нас сейчас не интересуют, они приведены просто для комплекта)
Любая другая величина выражается через использование этих семи. Например, скорость выражается как расстояние, преодолённое за время (метры в секунду, м/с), ускорение будет выражено как изменение скорости за единицу времени (метры в секунду за секунду или м/с²)
Как же выражаются используемые константы скорости света, гравитационной постоянной и постоянной самого Планка?
Скорость света (с) – это просто – м/с.
Постоянная Планка-Дирака (ħ) уже сложнее – исходя из определения, видно, что она имеет в себе единицы энергии, разделённые на частоту ħ = E / ω, где в числителе мы имеем энергию (Джоуль – это сила * расстояние, или 1 Дж = 1 Н•м=1 кг•м²/с²), а в знаменателе – частоту ([ω] = [2πf]) = Гц (раз в секунду или с⁻¹). Совместив единицы, мы получаем единицы измерения постоянной Планка (ħ): кг*м²/с.
Ну и гравитационная постоянная (G) выражается следующим образом:
Раз F = Gm1m2/r², то G = F r² / m1m2, то есть кг * м³ * c⁻² / кг² или м³ / кг * c²
Теперь, зададимся вопросом, а можем ли мы при помощи этих констант выразить длину?
Именно этот вопрос задал себе Макс Планк более 100 лет назад. Можно ли при помощи этих трёх фундаментальных констант создать новую единицу измерения длины? Трюк, который он придумал – записывать их как произведение G в какой-то степени α, ħ в какой-то степени β и с в какой-то степени γ:
Тогда его задача сводилась к определению степеней α, β и γ, таким, чтобы комбинации:
[c] = м с⁻¹
[ħ] = кг м² с⁻¹
[G] = кг⁻¹ м³ с⁻²
сводились бы просто к метрам.
Упрощаем:
Теперь, запишем левую часть уравнения в более подходящей форме:
Ну и теперь нам нужно просто сопоставить степени в левой и правой части уравнения, получив следующую систему:
0 = β – α
1 = 3 α + 2 β + γ
0 = –2α -β – γ
Первое уравнение говорит нам, что α = β, зная это , получаем:
1 = 3 α + 2 β + γ → 1 = 5 α + γ
0 = –2α -β – γ → 3 α = – γ
Следовательно, имеем α = 1/2 , β = 1/2, γ = – 3/2
Подставив значения степеней в формулу, мы обнаружим, что мы получили то же самое уравнение, что и раньше:
Планк не остановился на этом. Мы так же можем посчитать, а сколько массы нужно упаковать в этот объём, чтобы получить чёрную дыру. Нам всего только надо преобразовать полученное уравнение:
Эта величина получила название «Планковская масса».
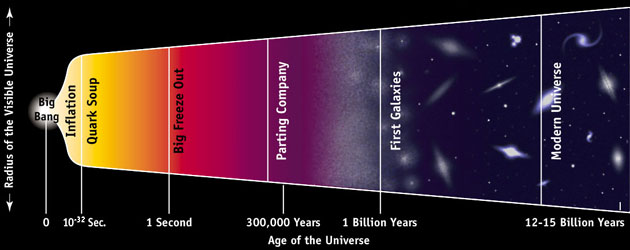
Есть так же «Планковское время» – строго говоря, время, за которое свет проходит расстояние равное «Планковской длине» (5,3 * 10⁻⁴⁴ с), но у этой величины есть и другое значение. Помимо того, что это – кратчайший интервал времени, который в принципе имеет физический смысл, это так же и кратчайший интервал, дальше которого мы никогда не сможем проникнуть в исследовании условий большого взрыва. Период с момента возникновения нашей Вселенной до 5,3 * 10⁻⁴⁴ с так и называется – Планковская эпоха.
Концепция самого времени теряет физический смысл на интервалах, меньше планковского времени!
Очень часто можно слышать вопрос «А что было до Большого взрыва?». Правда в том, что время не существовало как концепция на протяжении всей Планковской эпохи, как и не существовало никаких «до» (см. пост Правды и кривды теории Большого взрыва.).
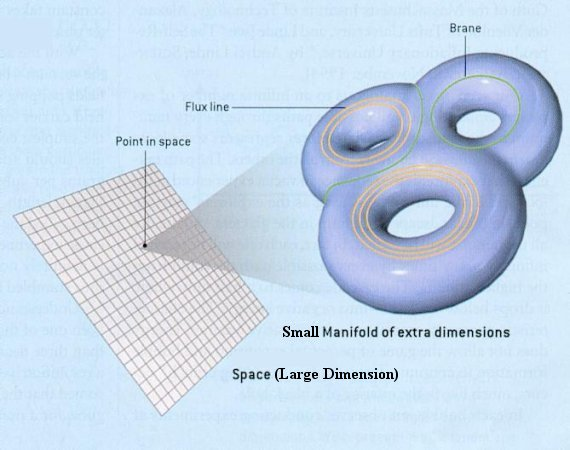
Теперь, уткнувшись в столь фундаментальный барьер, мы можем только гадать, является ли пространство-время непрерывным на любом интервале, мы лишь не можем ничего измерить на расстояниях, меньших Планковских, либо пространство-время дискретно, имеет «воксели» – мельчайшие кирпичики, и тогда самым наглядным аналогом подобной реальности станет популярная игра Minecraft, а пространства-времени в меньшем масштабе попросту не существует.
Планковская длина и планковское время: хранители тайн Вселенной
За последние 100 лет физики построили точные и действенные теории о Вселенной — от самого маленького до самого большого. Однако есть масштабы, на которых все эти теории не работают и которые хранят самые большие тайны о законах природы.
Мы привыкли жить в мире крупных, макроскопических вещей. Все, с чем сталкивается обычный человек в течение дня — от чашки кофе с утра до огромного огненного шара в небе под названием Солнце, — вещи, которые мы можем либо видеть, либо осязать. Однако еще в Древней Греции философы, в частности Демокрит и его учитель Левкипп, предположили, что все состоит из мельчайших неделимых частиц — атомов (в переводе с греческого буквально означает «неделимый»).
Со временем был открыт атом, а затем и его свойство, что он вовсе не неделимый, а состоит из ядра и вращающегося вокруг него электрона. Затем выяснилось, что и ядро состоит из протонов и нейтронов. Еще позже были открыты кварки, из которых состоят протоны и нейтроны атомных ядер. Эти миниатюрные частицы называют элементарными. Помимо кварков, среди элементарных частиц есть уже упомянутые электроны, бозоны, нейтрино и фотоны. Все они считаются теми самыми древнегреческими «атомами» — неделимыми.
В 1899 году (в некоторых источниках — в 1900-м) немецкий физик и по совместительству основоположник квантовой теории Макс Планк предложил особую меру измерения — планковские единицы. Это единицы, предназначенные для упрощения определенных алгебраических выражений, присутствующих в теоретической физике, в частности в квантовой механике. В число их входят такие фундаментальные единицы, как планковская масса, планковская температура, планковская длина и планковское время. В этом материале мы рассмотрим планковскую длину и планковское время и попробуем сделать это наиболее понятным способом, без сложных математических выкладок (хотя некоторые формулы нам понадобятся).
Как вы уже знаете, физика занимается изучением не только огромных космических структур вроде галактик и туманностей, но и невероятно маленькими явлениями на атомном и субатомном масштабах. Однако существует еще одна реальность в масштабах, которые намного меньше того, что науке удалось изучать. На этом уровне есть величина, настолько сильно выходящая за рамки традиционного понимания «маленького», что ее тяжело представить. Это планковская длина — она в 1020 раз меньше диаметра ядра атома водорода. Предполагается (или, точнее сказать, подозревается), что именно на этом уровне формируется «пена» пространства-времени. Чтобы осознать, о какой величине идет речь, можно заглянуть в анимацию «Масштаб Вселенной» по этой ссылке.
И все же о каких размерах идет речь? Планковская длина составляет всего 1,616 х 10-35 метра. Вычислить ее можно при помощи уравнения, включающего в себя целых три фундаментальные константы — постоянную Планка (6,6261 х 10-34), скорость света в вакууме (2,29979 х 108 м/с) и гравитационную постоянную (6,6738 х 10-11):
lP = √ħG/c3
Впервые Макс Планк пришел к этой примечательной единице после работы над излучением черного тела и квантовой механики. Вероятно, вы слышали, что это самая малая возможная длина.
Тут, как и в случае с древнегреческой концепцией атома, можно сказать: «Конечно, если у меня есть некая длина и я разделяю ее пополам, а затем повторяю это снова и снова, я буду получать все меньшие и меньшие значения». Однако мы говорим о масштабах, на которых физика уже не способна делать то же, что и математика. Один из самых ярких примеров таких невозможностей — движение со сверхсветовой скоростью. То есть на бумаге вы можете применить к массе силу и ускорить ее до скорости света и выше, но нам известно, что в природе это попросту физически невозможно, поскольку масса объекта (а значит, и энергия, необходимая для его ускорения) возрастает бесконечно. Получается, мы не способны осуществить в реальности все, что можем сделать на бумаге.
Теория струн предсказывает существование струн, составляющих все элементарные частицы, именно в масштабах планковской длины / © Universe Review
Итак, каким образом такая малая величина вписывается в физику? Если две частицы разделены планковской длиной или еще меньшим расстоянием, то невозможно определить позиции каждой из них. Более того, любые эффекты квантовой гравитации на этом масштабе (если они вообще есть) неизвестны науке, так как там само пространство не определено должным образом. В некотором смысле можно сказать: даже если бы мы разработали методы измерений, способные «заглянуть» в эти масштабы, мы никогда не смогли бы измерить что-либо меньшее, вне зависимости от дальнейшего совершенствования наших методов и оборудования.
Согласно стандартной космологической модели Вселенная родилась в результате Большого взрыва, начавшегося в бесконечно плотной точке. Особенно интересно то, что физики и космологи не имеют ни малейшего понятия, какие законы физики господствовали во Вселенной, прежде чем она превысила по своим размерам планковскую длину, так как еще нет подтвержденной теории квантовой гравитации. Тем не менее эта единица оказалась полезной во множестве разных уравнений, которые помогли вычислить и исследовать некоторые из самых главных тайн Вселенной.
Например, планковская длина — ключевой компонент в уравнении Бекенштейна и Хокинга для расчета энтропии черной дыры. Струнные теоретики считают, что именно на этом масштабе существуют «вибрирующие» струны, из которых состоят элементарные частицы Стандартной модели. Вне зависимости от того, верна теория струн или нет, с уверенностью можно сказать одно: в поиске объединенной теории всего понимание планковской длины и связанной с ней физики сыграет ключевую роль.
Самые первые моменты существования Вселенной в космологии называют планковской эпохой / © University of Illinois
А что насчет планковского времени? Если в двух словах, то планковское время — это время, за которое свет в вакууме проходит планковскую длину. Следовательно, эти две величины связаны между собой. Любопытно, что для вычисления планковского времени необходимы постоянная Планка, гравитационная постоянная и скорость света в вакууме. Точное значение планковского времени — 5,391 х 10-44 секунд, а вычисляется оно по формуле:
tP = √ħG/c5
Планковское время также называют квантом времени — самым малым значением времени, имеющим какое-то фактическое значение. Меньшие значения времени не имеют никакого смысла. Возвращаясь к теоретическим гипотезам, струнные теоретики предполагают, что струны размером в планковскую длину вибрируют с периодичностью, соответствующей планковскому времени. В 2003 году при анализе снимков Deep Field с телескопа «Хаббл» некоторые ученые высказали предположения, что если бы на планковском масштабе присутствовали флуктуации пространства-времени, то изображения очень далеких объектов были бы размытыми. Снимки «Хаббла», как они утверждали, были слишком точными, что, по мнению специалистов, ставило под сомнение концепцию планковских масштабов. Другие представители научного сообщества не согласились с этим предположением, отметив, что такие флуктуации были бы слишком малы, чтобы их можно было наблюдать. Кроме того, было высказано предположение, что ожидаемая размытость была устранена большими размерами объектов на снимках.
Снимок Hubble Ultra-Deep Field / © NASA/ESA/R. THOMPSON
Итак, планковская длина и связанное с ней планковское время определяют масштабы, на которых современные физические теории перестают работать. Вся геометрия пространства-времени, предсказанная Общей теорией относительности, перестает иметь всякий смысл. Эти масштабы хранят еще неоткрытую теорию, объединяющую Общую теорию относительности и квантовую механику, которая сможет наиболее полно описать законы физики. В сущности говоря, именно по этой причине современные описания развития Вселенной начинаются только спустя 5,391 х 10-44 секунд после Большого взрыва, когда Вселенная была размером 1,616 х 10-35 метров.
На вопрос ответит мой шофер
Макс Планк, получив Нобелевскую премию по физике, отправился в турне и всюду выступал с одним и тем же докладом. Его шофер сидел в зале и запомнил текст наизусть. А затем предложил пошутить: пусть он, шофер, выступит с докладом, а Планк посидит в зале в шоферской фуражке. Идея рассмешила Планка, и он согласился.
И вот шофер выступает с докладом по квантовой механике. Один профессор физики задает вопрос. Шофер выслушивает и говорит: «Никогда бы не подумал, что в таком прогрессивном городе мне зададут такой простой вопрос. С вашего позволения, я попрошу ответить на него своего шофера».
Из книги «Искусство ясно мыслить». Рольф Добелли
UPD: Это байка, где раввина подменили на Планка #comment_172371574
Макс Планк. Вперёд к Богу!
В одном из своих главных трудов, «Куда идет наука?» (1932), Планк отмечал:
«Невозможно противопоставить религию и науку, поскольку они дополняют друг друга. Наверное, каждый серьезный и мыслящий человек осознает, что необходимо признавать и развивать религиозный элемент его природы, дабы все силы человеческой души слились в совершенной гармонии. Не случайно величайшие мыслители всех времен были людьми глубоко религиозными». (Planck 1977, 168).
===========
«Меня как физика, то есть человека, посвятившего всю жизнь совершенно прозаической науке — исследованию материи, — никто не назовет фантазером. Я изучал атом и могу сказать: не бывает материи самой по себе! Вся материя возникла и существует только благодаря силе, которая приводит в движение частицы и удерживает их в виде мельчайшей солнечной системы — атома.
Но так как во всей вселенной нет ни разумной, ни вечной энергии, то нам следует предположить, что за этой энергией стоит Дух, обладающий разумом и самосознанием. Этот дух есть первопричина всей материи!» (Цит. по: Eggenstein 1984, Part I; см. также «Materialistic Science on the Wrong Track»).
Ссылка на доклад Макса Планка сделанный им в 1937 году.
Цитаты. Макс Карл Эрнст Людвиг Планк (Max Karl Ernst Ludwig Planck)
Макс Карл Эрнст Людвиг Планк (нем. Max Karl Ernst Ludwig Planck; — немецкий физик-теоретик, Лауреат Нобелевской премии по физике (1918)
Научные труды Планка посвящены термодинамике, теории теплового излучения, квантовой теории, специальной теории относительности, оптике. Он сформулировал второе начало термодинамики в виде принципа возрастания энтропии и использовал его для решения различных задач физической химии. Применив к проблеме равновесного теплового излучения методы электродинамики и термодинамики, Планк получил закон распределения энергии в спектре абсолютно чёрного тела (формула Планка) и обосновал этот закон, введя представление о квантах энергии и кванте действия. Это достижение положило начало развитию квантовой физики, разработкой различных аспектов которой он занимался в последующие годы («вторая теория» Планка, проблема структуры фазового пространства, статистическая механика квантовых систем и так далее). Планк впервые вывел уравнения динамики релятивистской частицы и заложил основы релятивистской термодинамики. Ряд работ Планка посвящён историческим, методологическим и философским аспектам науки.
Награды и членства:
Медаль Гельмгольца (1914)
Орден «За заслуги в науке и искусстве» (1915)
Нобелевская премия по физике (1918)
Медаль Лоренца (1927)
Медаль Франклина (1927)
Adlerschild des Deutschen Reiches[de] (1928)
Медаль Макса Планка (1929)
Медаль Копли (1929)
Медаль и премия Гутри (1932)
Медаль Гарнака[de] (1933)
Премия Гёте (1945)[180]
Почётный гражданин Киля (1947)
Член Прусской, Баварской, Гёттингенской, Дрезденской академий наук
Иностранный член Академии наук СССР (1926), Лондонского королевского общества (1926), Национальной академии наук США, Академии деи Линчеи, Австрийской, Датской, Ирландской, Финляндской, Греческой, Нидерландской, Венгерской, Шведской академий наук
Почётный доктор университетов Франкфурта, Ростока, Граца, Афин, Кембриджа, Лондона, Глазго, технических университетов Берлина и Мюнхена
Книги:
Planck M. Das Princip der Erhaltung der Energie. — Leipzig, 1887 (5 Aufl. — 1924). Русский перевод: Планк М. Принцип сохранения энергии. — М., Л.: ОНТИ, 1938. — 236 с.
Planck M. Grundriß der allgemeinen Thermochemie. — Breslau, 1893.
Planck M. Vorlesungen über Thermodynamik. — Leipzig, 1897 (4 Aufl. — 1922). Русский перевод: Планк М. Термодинамика. — М., Л.: Госиздат, 1925. — 310 с.
Planck M. Vorlesungen über die Theorie der Wärmestrahlung. — Leipzig, 1906 (5 Aufl. — 1923). Русский перевод: Планк М. Теория теплового излучения. — М., Л.: ОНТИ, 1935. — 204 с.
Planck M. Acht Vorlesungen über theoretische Physik, gehalten an der Columbia Univ. New York. — Leipzig, 1910. Русский перевод: Планк М. Теоретическая физика: Восемь лекций, читанных в Колумбийском университете Нью-Йорка весной 1909 года. — СПб., 1911. — 158 с.
Einführung in die theoretische Physik («Введение в теоретическую физику»):
Planck M. Band I: Einführung in die allgemeine Mechanik. — Leipzig, 1916 (4 Aufl. — 1928). Русский перевод: Планк М. Общая механика. — М., Л.: Гостехиздат, 1932. — 200 с.
Planck M. Band II: Einführung in die Mechanik deformierbarer Körper. — Leipzig, 1919 (3 Aufl. — 1932). Русский перевод: Планк М. Механика деформируемых тел. — М., Л.: Гостехиздат, 1932. — 184 с.
Planck M. Band III: Einführung in die Theorie der Elektrizität und des Magnetismus. — Leipzig, 1922 (2 Aufl. — 1928). Русский перевод: Планк М. Теория электричества и магнетизма. — М., Л.: Гостехиздат, 1933. — 183 с.
Planck M. Band IV: Einführung in die theoretische Optik. — Leipzig, 1927 (2 Aufl. — 1931). Русский перевод: Планк М. Оптика. — М., Л.: Гостехиздат, 1934. — 164 с.
Planck M. Band V: Einführung in die Theorie der Wärme. — Leipzig, 1930. Русский перевод: Планк М. Теория теплоты. — М., Л.: ОНТИ, 1935. — 228 с.
Planck M. Erinnerungen. — Berlin, 1948.
Planck M. Physikalische Abhandlungen und Vorträge (Bd. 1—3). — Braunschweig, 1958.
https://ru.wikipedia.org/wiki/%D0%9F%D0%BB%D0%B0%D0%BD%D0%BA...
Непридуманные байки 299 "Юноша, вы ещё слишком молоды..."
Когда Макс Планк стал профессором Берлинского университета, ему был 31 год. Он был очень худ, скромен и носил тоненькие усики, в отличие от других профессоров, носивших пышные бакенбарды и бороды. Планк еще плохо ориентировался в новом для себя здании и однажды забыл, в какой аудитории ему следует читать лекцию. Тогда Планк решил обратиться к пожилому заведующему канцелярией с вопросом:
"В какой аудитории профессор Планк сегодня читает свою лекцию?"
Старик снисходительно похлопал Планка по плечу:
"Юноша, не ходите туда. Вы еще слишком молоды, чтобы понимать лекции нашего мудрого профессора Планка".
«Благодаря открытию квантов энергии»
Мир стремительно меняется и наука - одна из областей нашей жизни, где это видно особенно отчетливо. Или – нет? В наши дни научное сообщество рассуждает о возможностях генной инженерии в области борьбы с раком, исследует гравитационное «эхо» Большого взрыва, строит квантовый компьютер. А над чем ломали головы ученые сто лет назад (по историческим меркам срок-то не такой уж большой)? Предлагаем вспомнить некоторые эпизоды научной жизни 1918 года и оценить, насколько человечество продвинулось в деле познания и освоения окружающего мира с тех пор.
Начнем с физики. Физика к 1918 году продвинулась довольно далеко. Уже вышел ряд работ Эйнштейна по теории относительности (в т.ч. была опубликована знаменитая формула E=mc2). Эксперименты Резерфорда и Гейгера по рассеянию альфа-частиц в тонких пластинках показали наличие внутри атома компактной структуры — атомного ядра. Их новая теория объясняла, в частности, существование изотопов. Было немало и других открытий.
Но кому же досталась главная научная награда – Нобелевская премия 1918 года?
Время было непростое: завершалась Первая мировая война, с карт мира исчезали целые государства, причем, не последние в списке мировых держав. Но Нобелевский комитет нашел возможность присудить премии за 1918 год. Правда, «задним числом» - в следующем, 1919 году (а вручили ее и вовсе летом 1920 года) и только по двум номинациям – по физике и по химии. Нас сегодня интересует первая номинация.
В том году на получение ставшей уже престижной премии претендовало почти тридцать ученых. В этом списке хватает имен, знакомым нам по школьным учебникам: Нильс Бор (получил премию позже, в 1922 году), Альберт Эйнштейн (удостоен премии в 1921 году), Хендрик Лоренц (уже награжденный премией в 1902 году), Жан Перрен (нобелевский лауреат 1926 года) и другие.
А победителем стал немецкий ученый Макс Карл Эрнст Людвиг Планк.
К тому времени Планка включали в список номинантов десятый год подряд. И вот, наконец, он из номинанта стал лауреатом. А ведь тоже могло быть иначе. Помимо мощных конкурентов в списке претендентов, против него могли сыграть и политические мотивы. Нобелевский комитет регулярно обвиняли и обвиняют в некоторой политической ангажированности и не зря. А Планк в этом плане был довольно уязвим.
Немецкий ученый, воспитанный в духе прусского патриотизма, с воодушевлением воспринял начало Первой мировой войны. В своих публичных выступлениях он приветствовал войну, направленную, как он думал, на защиту жизненно важных ценностей немецкой нации, и призывал молодёжь вступать добровольцами в армию. Правда, вскоре его пыл несколько утих, и он стал прилагать массу усилий для сохранения международного научного сотрудничества. А в 1916 году на фронте погибает его старший сын, что еще сильнее подтолкнуло ученого к пересмотру своей позиции.
Но то политика, а в тот раз, к счастью, решающее слово сыграла наука. Научные достижения Планка хорошо известны. Еще в 1900 году он выдвинул идею о том, что энергия излучается не непрерывно, а в виде порций – квантов. Впоследствии эта идея выросла в целую научную дисциплину – квантовую механику, причем развивалась она так быстро и порой непредсказуемо, что в поздние годы жизни Планк признавал: сам он не успевает за последствиями своих открытий.
Идеей квантового излучения его вклад в физику далеко не исчерпан: он сформулировал второе начало термодинамики в виде принципа возрастания энтропии, получил и обосновал закон распределения энергии в спектре абсолютно чёрного тела (формула Планка), впервые вывел уравнения динамики релятивистской частицы и заложил основы релятивистской термодинамики. И еще много чего.
Но Нобеля ему дали как первому среди отцов-основателей квантовой теории, значение которой для ученых того времени было уже неоспоримым. Официальная формулировка гласила: «В знак признания его заслуг в развитии физики благодаря открытию квантов энергии».
Насколько весомым выглядит вклад немецкого физика в науку на расстоянии века и как далеко человечество продвинулось в постижении квантовой теории с тех пор – рассказывает с.н.с. Института физики полупроводников СО РАН, доцент НГУ и НГТУ Илья Бетеров:
– Вместе с теорией относительности Эйнштейна это открытие фактически создало современную физику. Постоянная Планка [h] задает масштаб микромира, так же как и скорость света [с] определяет масштабы глобальных явлений во Вселенной. Возникнув как решение глубоко частной проблемы – описания спектра излучения абсолютно черного тела, где никак не удавалось добиться согласия теории и эксперимента, теория Планка полностью изменила наше представление о том, как устроен мир. Вместо детерминированного и непрерывного, он оказался дискретным и случайным. Квантовые явления лежат в основе множества современных технологий – от атомной энергетики до лазеров и микроэлектроники, но мы так и не стали понимать их интуитивно. Случайность результатов измерения, квантовые суперпозиции и перепутанные состояния остаются предметом научных дискуссий.
В последние десятилетия в развитии квантовой физики начался новый этап. Появились экспериментальные методы, которые позволяют управлять квантовыми состояниями отдельных квантовых систем – фотонов, атомов, ионов, сверхпроводящих интерферометров. Благодаря развитию нанотехнологий ученые стали создавать искусственные квантовые системы – квантовые ямы, квантовые нити, квантовые точки. Возникла концепция квантовых вычислений, под которым понимают сложные преобразования состояний многочастичных квантовых систем. Продолжаются попытки найти связь между гравитацией, которая задается геометрией макромира, и квантовыми явлениями в микромире. На этом пути развивается квантовая метрология, целью которой является повышение точности измерений за счет квантовых явлений.
И сегодня квантовая физика – это передний край науки. Эксперименты в современной квантовой физике могут делаться и на небольшом лабораторном столе, и в Большом адронном коллайдере. Их объединяет постоянная Планка и незабываемое ощущение, что находишься на границе неизведанного.
Конечно, как уже говорилось выше, в 1918 году физика жила «не квантом единым». В этом году начала работу Доминьонская астрофизическая обсерватория, расположенная в канадском городе Виктория. В ней разместили второй по величине в мире на тот момент телескоп, апертура которого составляет 72 дюйма (1,8 метра). А первым директором обсерватории стал известный канадский астроном Джон Стэнли Пласкетт. В ней он на протяжении многих лет вел программу определения лучевых скоростей звезд, результаты которой сыграли большую роль в открытии вращения Галактики и определении его параметров.
А еще в этом году присудили последнюю Ломоносовскую премию, которая была учреждена правительством Российской империи 8 марта 1865 г., в канун столетия со дня смерти М.В. Ломоносова «в память о заслугах, оказанных им отечественному просвещению». Иногда ее смешивают с премией им. М. В. Ломоносова, присуждаемой МГУ, но это совсем другая награда. Премия в 1000 рублей (немалая по тем временам сумма) вручалась «за особенно важные изобретения и открытия, сделанные в России в области промышленности и технических наук, и за лучшие сочинения». Лауреатов премии определяла Академия наук, при этом на Ломоносовскую премию распространялось общее академическое правило, не допускавшее действительных членов Академии к соисканию награды (для объективности).
Последним лауреатом Ломоносовской премии стал в 1918 году физик, ректор Института инженеров путей сообщения А.А. Брандт (за труд «Основания термодинамики»), но денег он уже не получил, поскольку и Академия наук этими средствами не располагала. На том премия свое существование прекратила.
Развитие авиации в военные годы привело к быстрому прогрессу аэродинамики и теории полёта, в чём велика заслуга Н.Е. Жуковского. За два года до этого он возглавил расчётно-испытательное бюро при аэродинамической лаборатории Московского технического училища, в котором разрабатывались методы аэродинамического расчёта и расчёта прочности самолётов. И успел опубликовать первые результаты работы. В частности, в 1918 году вышла его книга «Изследованiе устойчивости конструкцiи аэроплановъ». Эту проблему (с новых позиций) решают и современные авиаконструкторы. И надо сказать, что, хоть они далеко продвинулись с той поры, им еще есть над чем поработать.
Наталья Тимакова