Вопрос к лиге стоматологов
Увидел пост Стоматологи, хелп
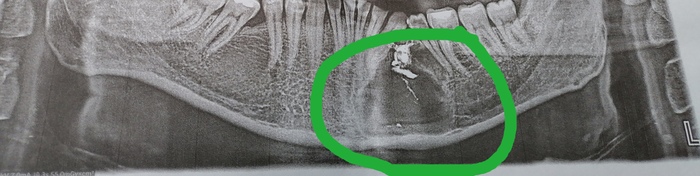
И решил задать вопрос. Недавно обнаружили кисту в челюсти. Большая, почти 3.5 см. Назначили операцию через 3 месяца. Может кто подскажет как делают подобные операции и как долго потом проходит лечение
Помощь со скворцом
Доброго дня. При ремонте крыши было нарушено гнездо скворцов. После попыток переместить гнездо в другое место в живых остался один птенец (если интересно, могу после написать), который сейчас находится дома, хорошо ест и неплохо себя чувствует. Однако вроде как пишут, что после того, как он подрастёт, отправлять его в дикую природу нельзя. Так ли это? И если так, то вдруг кто-то мечтает завести скворца, то мы можем отдать его, потому что не знаем что для него хорошо. Плюс мы живём в деревне и летом у нас весь день входная дверь открыта настежь, боимся, что он улетит и не выживет.
P.S.Мы живём в восточном Подмосковье.
Тактильный голод
Недавно у меня появился любимый человек, но возникла дилемма: у нас сильно различаются потребности в тактильности.
Я безумно люблю прикосновения и объятия в противовес ему.
Спрашиваю прямо:
-Нравятся ли это тебе?
-Нет.
-Тогда тебе неприятно, когда я тебя касаюсь? - в ответ сухое -Да норм.
Я понимаю, что у каждого свои потребности и важно соблюдать чужие границы, но в то же время я до одури хочу объятий и поцелуев.
Мы договорились не спешить, и я уважаю мнение партнёра, прошу говорить, если что-то доставляет дискомфорт, однако страдаю от этого сама.
Как быть?
Почему отрезок равен квадрату? Это доказанный в математике факт!
Вопросы бесконечности всегда вызывают живой интерес у аудитории. Сегодня я хочу рассказать Вам об удивительном, но простом геометрическом построении, известном еще в древней Греции, которое больше, чем через тысячу лет, стало предтечей исторического открытия Георга Кантора. Поехали!
Итак, еще древнегреческим геометрам было известно следующее занимательное построение:
Поясню: берем два отрезка AB и СD, через их концы проводим две прямые и отмечаем точку их пересечения E. Теперь мы можем провести целое семейство прямых из этой точки, которые пересекают два исходных отрезка в точках 1-3 (1'-3'). Древние греки сделали такой вывод: каждой точке отрезка AB сопоставляется точка отрезка CD.
Уже позднее, с развитием теории множеств, скажут, что древние греки построили биекцию (взаимно-однозначное соответствие) двух отрезков, что позволяет говорить об их равномощности. Иначе говоря, бесконечное количество точек в одном отрезке равно количеству точек в другом отрезке, несмотря на их разные геометрические размеры.
Великий Георг Кантор пошел дальше. Он доказал пародоксальное, казалось бы, утверждение: "в отрезке столько же точек, как и в квадрате". Вот как он это сделал:
Кантор взял произвольную точку квадрата с координатами
(0,x1x2x3x4....; 0,y1y2y3y4.....),
где под x и y понимаются цифры десятичной записи числа и сопоставил их точке отрезка с координатой
(0,x1y1x2y2x3y3x4y4...),
получившейся перемежением соответствующих цифр. Таким образом, Кантор установил биекцию между точками квадрата и отрезком. Более того, построив на таком квадрате куб, он показал равномощность куба и отрезка, затем обобщив всё на кубы высших измерений. Оказывается, какой размерности фигуру Вы бы не представили, точек в ней будет столько же, сколько в обычном отрезке!
Такому количеству точек Кантор приписал кардинальное число - Алеф-1, ставшее наименьшим несчетным бесконечным кардиналом.
Про бесконечные кардиналы, ординалы, множества и прочую ересь на максимально простом языке читайте в телеграмм-канале Математика не для всех.