sergeyshpadyrev

Продолжение первой части.

Лингвистическая относительность

После выхода в свет гравитационной теории Эйнштейна, идеи относительности приобрели невероятную популярность. В приложении к лингвистике они привели к популяризации гипотезы лингвистической относительности Сепира-Уорфа, утверждающей, что язык оказывает влияние на мышление, а в некоторых случаях полностью определяет его.

Классические примеры такого влияния:

• Если в одном языке больше слов для оттенков определённого цвета, чем в другом, то носители первого языка быстрее различают оттенки на границе цветов.

• В некоторых языках направление задаётся не словами прямо, налево, направо, а словами на север, на юг, на восток, на запад. Носители этих языков всегда, даже в помещении всегда знают направление на север.

• Носители разных языков по-разному распределяют время на пространственных осях. У европейцев будущее горизонтально правее прошлого, а у китайцев будущее вертикально выше прошлого.

• Частота использования в языке активного и пассивного залога грамматически задаёт вину и ответственность. В английском и русском более часто употребляется активное "разбил вазу", а в испанском пассивное "ваза разбилась". Это влияет на восприятие ситуации.

Один из самых дискутируемых аргументов в пользу гипотезы лингвистической относительности - исследование племени пирахан, живущих в джунглях Южной Америки:

Они ведут простую жизнь, их имущество обычно состоит из из горшка, кастрюли, ножа и мачете. В их языке нет числительных, времен и названий цветов, нет и языковой рекурсии, но зато существуют местоимения третьего лица для водоплавающих и неводоплавающих одушевлённых объектов.

В ходе проведенных этнологами и лингвистами экспериментов выяснилось, что из-за такой ограниченности языка носители племени пирахан не могут мыслить о прошлом и будущем, а также о других местах - они понимают только то, что происходит здесь и сейчас. Кроме того, обнаружилось, что для пирахан представляет огромную трудность счет предметов в количестве больше трех, у них нет декоративного искусства и они не умеют рисовать. Однако, существование в их языке местоимений для водоплавающих и неводоплавающих существ наводит на мысль, что их условия жизни и необходимое для выживания в этих условиях мышление влияет на ограничения и особенности их языка, а их язык в свою очередь влияет на их мышление.

Пирахан может заинтересовать что-нибудь необычное - например, пролетающий в небе самолет, однако как только тот скрывается из виду, они теряют всякий интерес к произошедшему, и даже не могут ответить на вопрос, видели ли они что-нибудь несколько секунд назад. Исследовавший их на протяжении долгих лет этнолог Дэниэл Эверетт писал, что люди племени пирахан руководствуются исключительно непосредственным опытом - они опираются только на ту информацию, которую получают от своих органов чувств в настоящий момент времени.

Этот аргумент обычно приводится в пользу сильной версии гипотезы Сепира-Уорфа, гласящей, что язык полностью определяет мышление - границы моего языка означают границы моего мышления. Обычно лингвисты придерживаются более слабой версии - язык влияет на мышление, но не полностью определяет его. Часто забывают, что в теории относительности не только геометрия пространства определяет движение материи, но и распределение материи определяет геометрию пространства. То же самое происходит и в лингвистике - не только язык влияет на мышление, но и мышление влияет на используемый язык, который в свою очередь обратно влияет на мышление.

При появлении у индоевропейцев колеса появилось языковое понятие "колесо", которое начали применять к описанию других аспектов окружающей действительности - появилась общая для всех индоевропейских народов идея цикличности бытия и специфическая для индийской ветви концепция колеса страданий Сансары. Изобретение в Шумере и Египте письменности и появление у финикийцев на землях пересечения шумерской и египетской цивилизации в Хаанане первого алфавита привело к общему для всех семитов почитанию священных писаний и идее о том, что в начале было слово. Древнегреческий философ Пифагор при работе над своей теорией музыки пришёл к идее о том, что планеты движутся по небу в ритме гармоничной музыки сфер. Развитие в Европе механики привело к идеям о том, что весь мир подобен огромному механизму, развитие биологии - к идеям о том, что Вселенная подобна живому организма, появление компьютеров к цифровой физике - к теории Вольфрама о том, что весь мир - это процесс вычисления информации, да и вообще, может, мы живём в компьютерной симуляции.

Но у всех подобных описаний мира как колеса, книги, механизма, живого организма или компьютера есть одна общая проблема - мы забываем, что за символом стоит что-то реальное, и скатываемся в игру самими символами и конструирование симулякров.

Симулякры

Симулякр — это вовсе не то, что скрывает собой истину, — это истина, скрывающая, что её нет. Симулякр есть истина.

Понятие "симулякр" вводит в своей работе "Симулякры и симуляции" великий французский философ-постмодернист Жан Бодрийяр. Симулякр, согласно определению Бодрийяра, - это копия копии копии символа. Сначала на карту языка наносится символ, отображающий какой-либо факт реальности. Потом создаётся новый символ, относящийся к первому символу так же, как этот первый символ относится к факту реальности, то есть снимается своего рода копия. Повторив эту процедуру несколько раз, мы получаем симулякр. Приведу пару цитат из своих прошлых эссе для прояснения.

Первый пример объясняет понятие симулякра на примере тыквенного латте:

Идеальный пример симулякра - это тыквенный латте в Старбаксе. Тыквы созревают поздно осенью. Из-за этого тыква стала символом осеннего урожая и скорой смены времени года. Старбакс выпустил свой фирменный тыквенный латте, доступный в продаже тольку осенью, на чашке с которым обычно нарисованы тыквы. Рецепт этого кофе долгие годы не содержал в себе никаких тыквенных ингредиентов, однако его вкус теперь у большинства клиентов Старбакс теперь накрепко связан именно с тыквами. Таким образом, у нас получается следующая цепочка: реальная материальная тыква -> визуальный образ тыквы -> символический образ тыквы как символа осени -> тыквенный латте в Старбаксе -> вкус тыквенного латте. Этот самый вкус накрепко ассоциируется у людей с тыквами, хотя не имеет к ним никакого отношения вообще.

Второй пример объясняет симулякры на примере религиозных идей:

Например, когда-то давно в попытках описать свои чувства, мы разделили ощущения на две категории - приятные (блаженство) и неприятные (страдание). Затем, описывая закономерности наступления последствий тех или иных поступков, люди придумали абстрактное понятие Бога, в котором выразили свои представления об основополагающем законе мира, и понятия рая и ада - состояний великого блаженства и великого страдания, одно из которых согласно законам мироздания служит как бы вознаграждением за правильные поступки, а второе наказанием за неправильные. Но наш ум терпеть не может чистые абстракции - он может воспринимать только идеи, воплощённые в визуальном образе. Так Бог, рай и ад превратились в массовом сознании в образы белобородого старика на троне, судящего человека по его поступкам и отправляющего того либо в сияющий град над облаками, либо в стоящий на огне котёл с кипятком, вокруг которого бегают хвостатые черти и протыкают варящихся там людей трезубцами.

По сути, симулякры - это падение вглубь фрактала языка. Бодрийяр различал три типа симулякров. Первый тип - знак, который ещё привязан к содержанию. Например, конкретный портрет конкретного человека. Второй тип возникает при серийном производстве - оригинал теряет привилегированное положение, разница между оригиналом и копией постепенно смывается, знак начинает замещать реальность. Например, массовый тираж журнала с фото модели на обложке - фото становится уже не просто знаком, отображающим конкретного человека, а знаком, выражающим успех или красоту, отвязываясь от конкретного реального человека. Третий тип - реальности больше нет, остаётся лишь сам знак: какое-либо знаменитое фото сводится к его упрощённому изображению, становящемуся знаком, выражающим какой-то символизм. Например, как изображение дискеты стало символом сохранения или знак доллара стал символом богатства. Знак больше не отображает реальность, а создаёт её - мы погружаемся в мир воображаемых сущностей, который сам Бодрийяр называл гиперреальностью.

Мы мыслим картинками райского града над облаками, серной камеры пыток под землей, бородатого Бога, и тем самым заключая себя в воображаемый мир символов, полностью оторванных от какого-либо содержания. Не стоит забывать, что икона - это образ божественного, делать идол из самой иконы неправильно. Именно эту мысль пытаются донести иконоборцы всех веков. Бог - не бородатый старик на небе, а кармический круговорот страданий - не колесо. Карту нельзя путать с изображённой на ней территорией.

В одной из своих книг русский востоковед Евгений Торчинов описывает учение буддийского философа Нагарджуны о языке:

Язык в принципе не может адекватно описать реальность, ибо все языковые формы неадекватны реальности. Неадекватно ей и философское мышление, оперирующее понятиями и категориями. Логическое мышление не в силах постичь реальность как она есть, а язык — описать её. Следовательно, никакая онтология, никакая «наука о бытии» невозможна, ибо она всегда будет связана не с реальностью, а с нашими представлениями о ней или даже с некоей псевдореальностью, сконструированной нашими мыслительными навыками и ложными представлениями. Всё реальное — неописываемо, всё описываемое — нереально.

Символы языка и явления реальности - не одно и то же. Вкусив плод с древа познания вместо плодов древа жизни, Адам и Ева были изгнаны из рая. Это тоже символический образ. Познание происходит через символы, жизнь живётся через непосредственный опыт переживания реальности. Заместить реальность её символами - и есть первородный грех. Как писал в одном из своих романов Виктор Пелевин:

Слова дали нам власть над миром, но заперли в тюрьме концепций. В этом и заключен смысл библейской метафоры изгнания из рая.

В другом своём романе он писал:

Все религии и духовные учения спорят между собой по множеству поводов, но сходятся в одном – объяснить человеку, что такое Бог, невозможно. Вернее, можно объяснить человеку концепцию Бога, и она станет частью его умственного багажа. Но это не значит, что человек познает Бога. Это значит, что на его горбу появится еще один чемодан барахла, который он понесет с собой на кладбище. Бога можно только непосредственно пережить.

Вторит Пелевину и великий британский философ Алан Уоттс:

Загадка жизни - это не проблема, которую нужно решить, а реальность, которую нужно пережить.

Структуры и их произвольность

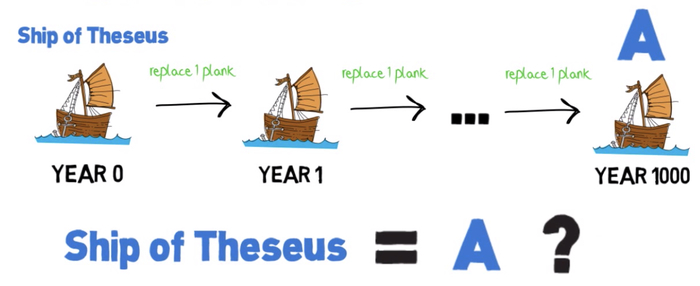
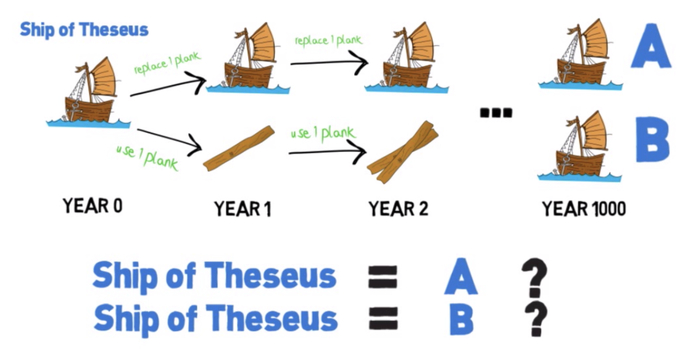
Важной вехой на пути лингвистической философии XX века стал структурализм, изучающий как именно структура языка влияет на наше мышление. Основоположник структурализма швейцарский лингвист Фердинанд де Соссюр ещё до Витгенштейна высказал несколько фундаментальных для лингвистичекого поворота идей: он заметил, что язык - это не набор имён для вещей, а система различий, в которой значение каждого слова определяется его местом в языке. Кот - это кот, потому что он не пёс, не стол и не дом.

Структура языка влияет на мышление человека. Человек ходит по территории, смотря на карту - если на карте нет тропинки, то человек по ней не пойдёт даже, если в реальности на территории она есть. Тут есть интересная аналогия с нейронными дорожками в мозге. Процитирую одну из своих заметок:

В кибернетике, науке о строении и функционировании систем, один из основных описательных инструментов - это понятие петли обратной связи. Положительная обратная связь - это когда последствия некоего процесса служат причинами ускорения проистекания этого процесса, а отрицательная обратная связь - это когда последствия процесса служат причинами замедления, остановки или даже обращения вспять проистекания этого процесса.

Отрицательная обратная связь нужна для стабилизации и поддержания гомеостаза. Потоотделение при перегреве тела помогает организму охладиться. Острая необходимость навыков какой-то профессии на рынке труда приводит к дефициту кадров, дефицит кадров приводит к повышению зарплат, повышение зарплат приводит к тому, что больше людей обучаются этой профессии, и, в конце концов, весь спрос на специалистов этой профессии удовлетворяется, дефицит исчезает, зарплаты падают, ситуация стабилизируется.

Положительная обратная связь нужна для того, чтобы было возможным обучение и адаптация системы и появление сложных структур. Хорошим примером положительной обратной связи служит гравитация - тяготение собирает материю в один центр масс, который начинает притягивать окружающую материю ещё сильнее. В капиталистической экономике гравитационной массой служит капитал - чем больше у тебя капитала, тем тебе легче зарабатывать ещё больше денег и увеличивать капитал. Или, например, наличие нескольких детей и страх за их будущее мотивирует людей к поиску стабильных оснований в жизни, что приводит их к религии, а религиозные учения поощряют заведение большего количества детей.

В человеческом и машинном обучении положительная и отрицательная обратная связь играют ключевую роль. Положительная связь состоит в награде за правильные ответы, а отрицательная - в наказании за неправильные. В итоге, после многократного получения различной обратной связи в уме человека или нейросети протаптываются определённые нейронные тропинки, мы начинаем понимать, что правильно и что неправильно, как надо и как не надо. Ребенок рождается с чистым умом. Обычно такое состояние называют tabula rasa - чистая доска. Во время обучения в уме ребенка протаптываются одни дорожки, по которым родители и учителя мотивируют его ходить, и зарастают сорной травой те места ума, где взрослые ему ходить запрещают. Многократное повторение превращает тропинки в борозды, с которых так просто не сойти - у взрослого человека тропинки ума уже настолько протоптаны, что выйти за их пределы для него становится почти немыслимо. Но откуда изначально появляется карта-план, по которой при обучении прокладывают тропинки? Откуда взрослые знают, куда уму детей идти нужно, а куда нет?

Французский философ Мишель Фуко считает, что это определяется дисциплинарной властью в конкретном обществе - традициями, устоями, общепринятыми паттернами мышления и поведения. Умы взрослых уже сформированы этим обществом и воспроизводят карту своих тропинок в умах детей. Их паттерны мышления могли быть сформированы целые поколения назад: некоторые из них имеют логичную объективную причину, некоторые сформированы случайно и воспроизводятся из поколения в поколение как родовые травмы - например то, что вашего прапрадеда раскулачили большевики, может сильно влиять на ваше отношение к финансам, даже если вы про своего предка и не знаете, вам просто передалось это через умы родителей.

Любая власть опирается на определённое представление о нормальном и желательном устройстве общества. Те же, кто не вписываются в эту картину, подвергаются дисциплинарному наказанию. Например, если в качестве нормы закрепляется требование быть умытым и причёсанным, то человек, нарушающий эту норму, вызывает раздражение не потому, что он причинил кому-то вред, а потому, что своим существованием он нарушает воображаемую картину порядка. У общества возникает желание этого невписывающегося в него человека куда-то деть, изолировать, и оно применяет насилие для приведения реальности в соответствие со своей нормой, помещая того либо в тюрьму, либо в психбольницу.

Чтобы перепрошить ум нужно осознанно многократно повторять применение других паттернов мышления - а это очень сложно. Буддийские монахи часто практикуют тренировку щедрости: они берут тарелку, полную разноцветных камешков, воображением убеждают себя, что эти камушки - самое ценное, что у них есть, и после одним движением руки рассыпают их вокруг себя. Многократное повторение этой тренировки формирует новые нейронные связи в их мозге, то есть перепротаптывает те самые дорожки в уме. Когда монах попадает в ситуацию, в которой нужно проявить щедрость и отдать последнее, он делает это без усилия воли. Другой управляемый способ перехода на другие дорожки - это долгие размышления об основаниях своих убеждений, попытка проследить все свои мысли до их источников. Что-то вроде динамической медитации випассаны, при которой медитирующий отслеживает возникновение и угасание своих мыслей и чувств.

Есть ещё несколько неуправляемых процессов перехода на другие дорожки ума - шизофрения, хроническая депривация сна и употребление психоделиков (наркотики, запрещены в РФ). Все эти вещи, очевидно, крайне вредны для ментального здоровья человека. Эффект на мозг шизофрении и психоделиков схож. Представьте себе, что протоптанная в мозгу нейронная дорожка - это не просто борозда, а глубокое русло, по которому течёт река. И тут в эту реку падает дерево и перекрывает русло. Река тут же выходит из берегов, затапливает всё вокруг и сотни ручейков текут во все стороны, прокладывая новые русла. Ум одновременно идёт по куче непротоптанных дорожек, вызывая чувство эйфории от единства всего со всем и полного единения со Вселенной. Из-за желания повторения этого чувства психонавты подсаживаются на психоделические наркотики и постепенно выжигают себе мозги. Шизофреники просто сходят с ума, их поведение становится непредсказуемо опасным, а логика их действий не поддаётся пониманию здорового человека. И тех, и других, в полном соответствии с философией Фуко, заталкивают в спецучреждения.

Однако чисто логически, строгой линии демаркации между здоровым человеком и шизофреником, между нормальностью и безумием нет - это всегда искусственно проведённая граница в виде принятой в конкретном обществе нормы. Человек, который всегда ходит по протоптанным нейронным дорожкам своего ума, хорошо действует внутри общественной системы, но принципиально не способен к творческому выходу за её границы. Вы замечали, что яркая способность к творчеству в людях всегда идёт рука об руку с безумием? Ведь безумие - это использование нестандартных дорожек, прогулка по вольчим тропам ума. Гений всегда безумен, но не каждый безумец - гений.

Второй важной вехой в лингвистической философии стал постструктурализм. Философы-постструктуралисты заметили, что сам язык никогда не бывает совершенно статичным - язык динамичен и постоянно меняется. Язык развивается, слова меняют значения, оттенки смыслов смещаются друг относительно друга. Кроме того, язык не один - их чрезвычайно много. Разные дискурсы говорят на своих собственных языках и тем самым рисуют свои собственные карты реальности.

Можно сказать, что структурализм подобен игре в шахматы - шахматные фигуры могут двигаться по доске только согласно определённым правилам. Мы можем изучать возможные в этих правилах дебюты и эндшпили. Постструктурализм же задаёт вопросы про сами правила. А кто придумал эти правила? Почему правила именно такие? Можно ли играть иначе?

Французский философ-постструктуралист Жак Деррида писал, что любую структуру можно деконструировать, разобрать на отдельные детали, выделить из каждого символа траекторию его конструирования и пересобрать всё в совершенно новую структуру. Постструктуралисты пытаются показать людям, что возможны другие тропинки - есть не только классические шахматы, но есть и шахматы Фишера с те ми же правилами ходов, но разными изначальными расстановками фигур, есть трёхмерные шахматы, есть шахматы с туманом войны. Все правила равны - привилегированной системы правил нет. Конечно, укоренившиеся в общественном сознании правила, структура языка и паттерны мышления обладают огромным гравитационным притяжением, от которого так просто не сбежать. Но постструктуралисты, подобно русским космистам начала XX века, предлагают вырваться из этого гравитационного колодца и познать Вселенную во всей её божественной полноте.

Послесловие

Однако у постструктурализма есть огромный изъян - он хорошо работает как критический метод, как интеллектуальный скальпель по деконструкции укоренившихся символьных систем и соотвествующих им властных отношений, но как полноценная философия несостоятелен, ведь его основной принцип подрывает сам себя. Если нет никакой привилегированной системы правил, никакой единственно верной языковой карты тропинок, отображающей территорию фактов, то получается, что нельзя сказать, что сам постструктурализм - это не просто один из таких языков, ничем не лучше и не хуже других.

Постструктурализм отрицает абсолютную необходимость существования какой-либо привелегированной системы отсчёта - любые правила и структуры мышления произвольны. Но он не может объяснить, почему это отрицание само не произвольно. Классическая проблема нигилизма - если ничто не имеет смысла, то и сам нигилизм не имеет смысла. Эту проблему постструктурализма пытается решить французский мыслитель Квентин Мейясу в своей философии спекулятивного реализма. Мейясу утверждает абсолютную точку отсчёта: онтологически нет необходимостей, кроме одной - нет ничего необходимого. Правило только одно - никаких правил. Нет абсолютных смыслов, структур и оснований - и это единственное абсолютное утверждение, та точка, с которой начинается рисование любой карты.

Буддийская философия идёт другим путём: она соглашается с тем, что привилегированных языков, систем мышления, дискурсов и интерпретаций нет, но не возводит это утверждение в абсолют. Буддизм говорит, что проблема не в том, что привилегированной системы отсчёта нет, а в том, что мы желаем, чтобы она была, и в этом кроется корень наших страданий. А истина не в системах мышления, а в другом. Вот смотри какой цветок лотоса! Как же он красив!

Мы привыкли думать, что язык — всего лишь инструмент описания реальности, нейтральное зеркало мира. Но что, если всё наоборот: что если не мы говорим языком, а язык говорит нами? Что если символы и знаки не просто передают мысли — они заранее очерчивают границы того, что вообще может быть помыслено? В современном мире знаки всё чаще отрываются от обозначаемых ими вещей, начинают ссылаться сами на себя и создавать собственную реальность, в которой мы и живём, спорим и принимаем решения. Может быть и правда "в начале было слово", как писал об этом Иоанн Богослов?

В этом эссе мы поговорим о том, как используемый нами язык формирует систему нашего мышления, как размышление о своём мышлении меняет само это мышление, как на него могут влиять географические и исторические факторы, как мы пытаемся натянуть реальность на имеющиеся у нас символьные абстракции, как язык и мышление взаимодействуют в головах людей и больших языковых моделей, и как лингвистика изменила подход к философии.

Уровни мышления

В недалёком прошлом, лет десять назад, среди представителей среднего класса было очень модно уезжать на какое-то время в Тайланд или на Гоа на поиски духовного просветления, занятия йогой и випассаной. Конечно же, большинство таких поездок были просто туристическими аттракционами в стиле нью-эдж без какого-либо серьёзного изучения лежащей под этими занятиями философии. В массовом сознании, йога - это не вершина развития мысли одной из шести школ философии индуизма, как оно есть на самом деле, а просто гимнастика с дыхательными упражнениями на свежем воздухе. То же самое и с випассаной - в массовом сознании это не один из важнейших методов буддизма по освобождению ума от страдания, а просто медитации в ходе недельного ретрита с отдыхом от каменных джунглей и бега в мышином колесе. Мало кто из туристов-просветленцев понимает, в чём заключается суть випассаны. Поэтому давайте для начала разберемся с тем, что такое випассана, и какая мысль за ней стоит.

В буддизме практикуются три основных вида медитации:

• Шаматха - статическая медитация, в ходе которой практикующий концентрирует своё внимание на каком-либо объекте или ритме, например, на дыхании, и пытается не думать ни о чём другом. Ум постоянно пытается соскочить и начать думать на отвлечённые темы. Мысли так и лезут в голову - стоит задуматься о чём-то другом на секунду, и за одной мыслью цепочкой идёт вторая, за второй - третья. Как только практикующий замечает, что его ум отвлёкся, он немедленно возвращает своё внимание к объекту медитации. Это помогает успокоить ум и очистить его на время от мыслей, переживаний и прочей ментальной грязи.

• Випассана - динамическая медитация, в ходе которой практикующий не пытается избавиться от снующих в его голове мыслей, а наоборот даёт им волю и просто наблюдает, как мысли возникают, продумываются и исчезают в его голове. Это как смотреть на летящие от костра искры. Практикующий пытается осознать то, из каких предпосылок определённая мысль появилась, почему он испытывает по отношению к чему-то именно такую эмоцию, а не какую-то другую. Випассана помогает увидеть, что мы - не источник наших мыслей, не тот, кто их порождает. Мысли сами появляются и исчезают у нас в уме. Попробуйте специально начать думать о чём-то, и поймете, что это невозможно сделать с помощью усилия воли. Попробуйте перестать думать о чём-то, и поймете, что это тоже невозможно сделать усилием воли. Випассана помогает практикующему увидеть, что его мысли, его чувства и всё то, что как он думает составляет его "Я" - это лишь рефлективные отклики на триггеры во внешнем мире и в собственной психике.

• Метта - медитации любящей доброты, в ходе которой практикующий сознательно вызывает у себя чувство безграничной любви, радости и сострадания ко всему живому. Это помогает очистить ум от злобы, залить своё сознание ярким сияющим светом и протопать в мозге устойчивые нейронные связи позитивного мышления.

Таким образом, практикуя випассану, мы учимся понимать, что наш ум - это зеркало, а наши мысли, эмоции и мысли - это отражения. Мы учимся отслеживать путь возникновения определённых мыслей и состояний ума. Задавая себе вопросы "Почему я чувствую эту эмоцию?", "Почему мне в голову пришла эта мысль?", "Чего я в данный момент боюсь?", "Почему я сейчас гневаюсь?", "Почему мне сейчас тревожно?", "Почему мне сейчас тепло и радостно?" мы начинаем лучше понимать триггеры, которые приводят нас к тем или иным чувствам и мыслям. Мы начинаем отслеживать паттерны собственного мышления и понимаем, почему именно та или иная мысль пришла нам в голову. Мы размышляем о том, как именно мы мыслим, занимаемся метакогницией, чтобы точно понимать своё мышление принимать решения полностью осознанно, а не потому, что внешний раздражитель активировал какую-то автоматическую когнитивную программу ответа на него.

Недавно я наткнулся на интересные размышления о том, как в процессе изменения осознанности относительно собственного мышления и его ограничений меняется само это мышление:

• На первом уровне мышления, который характерен для ещё совсем маленьких детей, наши действия не отделены от мышления и полностью импульсивны. Мы злимся и тут же лезем драться.

• На втором уровне мы учимся отделять наше мышление от поведения. Мы сдерживаем наши действия, даже если в этот момент злимся. Учимся врать, понимая, что от нас хотят услышать другие.

• На третьем уровне мы формируем наше мировоззрение на основе того, во что верит наша группа - наша семья, наше окружение, наш социальный класс. То, что хорошо для General Motors, хорошо для Америки. Если моя семья - верующая, то я тоже буду верить в Бога, даже не думая, что может быть как-то иначе.

• На четвертом уровне мы учимся отделять своё мировоззрение от взглядов нашей группы - мы замечаем, что некоторые наши убеждения могут в чём-то расходиться с тем, как принято думать в нашем окружении. Мы начинаем сомневаться в наших убеждениях, считая, что их нам навязали.

• На пятом уровне мы учимся анализировать факты, теории, учения и учимся осознанно выбирать своё мировоззрение, свою веру, свои принципы, но наше мышление всё ещё остаётся чёрно-белым. Мы всё ещё считаем, что та картина мира, которую мы себе сами сформировали - единственно верная, а все остальные - дураки и не лечатся.

• На шестом уровне мы осознаём, что наши убеждения - это не объективная истина, а результат влияния среды, в которой мы находимся. Тут чёрно-белое мышление наконец-то ломается. Мы понимаем, что формирование наших взглядов на жизнь напрямую зависит от того, где мы выросли, кто наши родители, как у нас со здоровьем, какие у нас доходы. Например, молодые, здоровые и богатые более склонны к либертарианскому мышлению, старые, больные и бедные тяготеют к социализму. Мы учимся видеть мир в виде набора различных систем этических, политических, религиозных убеждений и взглядов, среди которых нет объективно верного. Разные системы возникают из разных условий, имеют свои причины, свои плюсы и минусы.

• На седьмом уровне мы учимся работать с системами, осознавая свое участие в них. Например, руководим организацией, понимая собственные "слепые зоны" и понимая, что наша точка зрения субъективна и сформирована предвзятостью, которую мы не можем видеть до конца. Мы начинаем понимать, что мы и системы взаимно влияем на друг друга.

• На восьмом уровне мы осознаём, что все эти системы - просто ментальные модели у нас в уме, полезные выдумки, мыслительные конструкты, символы, которыми оперирует наше мышление. Мы начинаем относится к нашим духовным убеждениям как к метафорам, а не буквальной истине. Учимся отличать символы от их значения

• На девятом уровне мы достигаем полного пробуждения: пропадает всякое разделение, мы видим систему, как единое целое, как один живой организм, в котором разные его части, разные системы выполняют свою роль, и их противостояние поддерживает гомеостаз. Мы становимся зеркалом - больше нет никого, кому нужно «кем-то становиться» — есть только присутствие, реагирующее на то, что возникает.

Это очень условная лестница уровней мышления, но она хорошо показывает, как постоянный выход за пределы текущего когнитивного паттерна помогает нам видеть картину всё шире и шире. На верхних уровнях этой лестнице мы начинаем мыслить кибернетически - системами, петлями позитивной и негативной обратной связи, реакцией и адаптацией. На шестом уровне мы пользуемся моделями кибернетики первого порядка, изучая системы как бы взглядом на них извне, а начиная с седьмого уровня используем кибернетику второго порядка, изучая системы изнутри, будучи наблюдателем внутри них, без «вида со стороны Бога»

Наш разговор в этом эссе пройдёт на шестом-девятом уровнях этой иерархии. Мы поговорим о языке, символах, значениях, влиянии языка на мышление и мышления на язык, коснёмся даже теологии. Но для начала я приведу пример двух различных систем мышления, определяющихся средой, чтобы было понятно о чём идёт речь в описании шестого уровня иерархии мышления.

География как приговор

Говорят, что география - это приговор. Имеется в виду, что особенности расположения страны на географической карте мира неизбежно ведут к определённым особенностям её внутренней и внешней политики. Особенности поведения людей и их убеждения в небольшой вечно солнечной Португалии будут резко отличаться от убеждений и поведения людей в громадной России с зимами по полгода. Более того, особенности рельефа местности, выход к морям и другие географические факторы всегда вынуждают политическое руководство страны к определённым действиям - география решает с кем мы дружим, а с кем постоянно воюем. Влияние географии на политику изучается геополитикой. Есть особенность геополитики, которую обычно забывают - география определяет не только политическую необходимость определённых действий, но и само мышление людей.

Возьмём, например, две великие империи XIX века - Британскую и Российскую. Британия - классическая морская талассократия, Россия - континентальная теллурократия. Если вы в те времена поговорили бы с политиками обеих империй, то обнаружили бы, что люди, смотря на одну и ту же карту мира, видят разные вещи. Русский видит землю на фоне воды, то есть континенты на фоне океанов, а англичанин наоборот видит воду на фоне земли, то есть морские пути на фоне берегов. Они оба смотрят на одну и ту же карту, но их внимание концентрирует их сознание на разных вещах. Островные государства и морские империи концентрируют своё внимание на океанах и мыслят морскими путями, а континентальные империи мыслят в первую очередь континентами и сухопутными путями. Эти типы мышления настолько разные, что даже в вооружённых силах армия и флот всегда разделены.

Кроме того, сама этика жителей островов и жителей суши существенно отличается. Не потому что одни злые, а другие добрые, а потому что география склоняет их к разным системам мышления. Крупные сухопутные державы при своём расширении реже устраивали тотальные геноциды, предпочитая включать покорённые территории в себя как часть метрополии, хоть и не всегда полноправную, и старались поддерживать дружественные отношения с покоренными народами. Это связано с тем, что сухопутная армия завязана на дорожную логистику - если у тебя плохие отношения с народами на окраинах твоей империи и ты отправился через их земли в заграничный поход, логистику тебе чуть что перережут и твою армию ждёт неминуемый разгром. Морские державы не зависят от отношений с покорёнными народами, ведь перерезать логистику в море гораздо сложнее - им важно контролировать проливы и ключевые узлы. Покоряемые морскими державами территории обычно располагались по берегам океанов, а пространство у берега всегда ограничено, поэтому с гораздо большей частотой они грабились, угонялись в рабство или попросту вырезались.

География влияет не только на экономический уклад и внутреннюю политику на покоренных территориях, но и на саму этику имперских народов, которая должна оправдать текущую экономическую модель. Этика - тоже производная от географии. В Британской морской империи Редьярд Киплинг написал своё знаменитое "Бремя белого человека", в котором все туземные народы описывались как полубесы-полудети, которым белый господин несёт свет цивилизации. В Российской сухопутной империи системного расизма в целом не практиковалось - типичной стратегией была инкорпорация элит, обращение в подданство, ассимиляция покорённых народов.

Первый лингвистический поворот колеса философии

Обычному человеку может казаться, что философы обсуждают одни и те же вопросы вот уже несколько тысяч лет. Но на самом деле, за последние полторы сотни лет произошли кардинальные изменения не только в науке, но и в философии. Самое важное из них - случившийся в начале XX века лингвистический поворот в мышлении.

До лингвистического поворота европейские философы обсуждали вопросы вроде "Что есть бытие?", "Что такое сознание", "Каковы вещи сами по себе?", и писали длинные труднодоступные для понимания многотомные трактаты на пространные темы. Особенно сильно графоманией страдали немецкие философы XIX века - видимо, именно поэтому внутри немецкой традиции и зародился этот самый лингвистический поворот. Австрийский философ Людвиг Витгенштейн, подобно мальчику в сказке Андерсена про голого короля, задал вопрос: "А что мы собственно обсуждаем?".

Согласно его "Логико-философскому трактату", мир состоит из фактов, а наш язык - это отображение этих фактов или, можно сказать, карта мира фактов. Любые утверждения, произнесенные или записанные на языке - это просто линия на этой карте. Следовательно, любой сложный философский вопрос вроде "Что есть сознание?" - это узел, заплетенный этой линией с самой собой. По мнению Витгенштейна, философия должна распутывать эти языковые узлы. При использовании такого лингвистического подхода становится легко понять, что многие вечные вопросы философии - это просто напросто ошибки грамматики в конструируемых нами предложениях.

Исходя из этого, вместе со своим близким другом, английским философом Бертраном Расселом, Витгенштейн пытался свести философский язык к математической логике с чётко определённой символьной грамматикой на основе, например, теории множеств. Операции над символами языка, подобно операциям линейкой и циркулем на карте, могут сказать нам что-то о реальности. Если символы языка, будь то слова естественного языка или символы языка математического, отображают факты реальности, то значит любые фигуры в пространстве языка изоморфны фигурам в пространстве фактов - записанная символами логически корректная цепочка утверждений должна приходить к выводу, наблюдаемому в реальности. Именно так, например, на кончике пера с помощью математики был открыт Нептун.

Если сущности, о которых идёт речь, не определены математически, то философствовать просто напросто не о чем. Как выразился сам Витгенштейн: о чём невозможно говорить, о том следует молчать. Единственный разумный способ философского размышления, согласно Витгенштейну, - это определить аксиомы философской системы, построить с помощью символов математической логики утверждения о чём-либо и строго математически либо доказать, либо опровергнуть эти утверждения. Если какое-либо утверждение нельзя сконструировать с помощью системы символов, то оно не стоит и рассмотрения. Витгенштейн верил, что если мы построим идеальный язык, то мир станет идеально нам ясен. Такой взгляд лёг в основу целого движения - аналитической философии.

Лёгким движением ума Витгенштейн подорвал наивный реализм по отношению к существованию называемых нами сущностей вроде "бытие", "сознание" или "время", поставил под вопрос любую объективную метафизику и связал философию с лингвистикой, логикой и когнитивистикой. Можно сказать, что "Логико-философский трактат" Витгенштейна стал аналогом специальной теории относительности Эйнштейна в философии, которой он вероятно и вдохновлялся в годы написания трактата. После совершенного переворота в мышлении Витгенштейн на долгие годы удалился от мира. Но спустя несколько десятилетий вернулся, чтобы совершить второй, ещё более радикальный лингвистический поворот, подобный уже общей теории относительности.

Второй лингвистический поворот колеса философии

Согласно "раннему" Витгенштейну, язык представляет собой карту территории мира реальных фактов. Спустя много лет "поздний" Витгенштейн в своей работе "Философские исследования" пришёл к более радикальной мысли - карта не одна, их бесконечно много. Дело в том, что любая карта по своему определению сильно сжимает информацию о изображённой на ней территории с помощью символов. Вместо города, мы рисуем на карте кружочек, вместо дорог рисуем линии. И в зависимости от того, какой аспект территории мы хотим описать, мы используем разные наборы символов - для топографической карты одни символы, для политической - другие, для карты почв - третьи. Если бы мы попытались описать территорию целиком, то пришли бы к абсурдной ситуации, описанной аргентинским писателем Хорхе Луисом Борхесом в рассказе "О точности в науке":

В этой Империи искусство картографии достигло такого совершенства, что карта одной провинции занимала целый город, а карта империи — целую провинцию. Со временем эти несоразмерные карты перестали удовлетворять, и коллегия картографов начертила карту империи, имевшую размер империи и точнейшим образом совпадавшую с ней. Менее приверженные к изучению картографии последующие поколения сочли, что столь пространная карта бесполезна, и не без непочтительности оставили ее на милость солнца и зимней стужи. В пустынях Запада остались еще разрозненные руины карты, в коих селятся дикие звери и нищие бродяги; во всей стране не осталось другого памятника географическим наукам.

Создавая карту, мы в любом случаем берём лишь определённый аспект территории и сильно сжимаем информацию. Если бы мы попытались воспроизвести по этой карте новую территорию, то построили бы копию, сильно отличающуюся от оригинала. Сжатие информации всегда ведёт к потери части этой информации. В этом и есть смысл абстрагирования.

У того же Борхеса в рассказе "Фунес, чудо памяти" описывается человек с гипермнезией, который в деталях помнит каждый день своей жизни. Это реально встречающееся у людей заболевание, ну или дар, это как посмотреть. Люди с гипермнезией часто испытывают проблемы с абстрактным мышлением, так как абстракция - это, по определению, процесс сжатия информации и превращения множества конкретных примеров в одну абстрактную схему явления. Гипермнезики просто помнят сотню конкретных примеров и малейшие их детали, поэтому им трудно абстрагировать. Память оказывает сопротивление абстракциям.

Витгенштейн пришёл к выводу, что языковых карт реальности может быть бесконечно много, и ни одна из них не полна, так как лежащий в основе любой карты символ - это всегда абстракция, а абстракции теряют часть информации. Каждый символ на карте имеет смысл только внутри принятой системы символов. Каждое слово имеет смысл только внутри принятой системы значений, которая описывает определённый аспект реальности.Язык не отображает факты, язык - это просто игра слов, оперирование символами по определённым правилам. Согласно его теории, значения слов определяются их употреблением внутри языковых игр.

Классический пример языковой игры - строитель кричит своему помощнику "Кирпич!", и помощник молча приносит тому кирпич. Тут видно, что у языковой игры есть правила - слово "кирпич" означает не конкретный предмет, а то, что нужно принести его. Значение слова зависит от того, как с ним обращаются. Если слово "кирпич" кричит пассажир водителю, оно означает совсем другое: остановись, там знак "въезд запрещён". Значение слова зависит от окружающего его контекста, от той языковой игры, внутри которой происходит взаимодействие. Часто мы используем слова в значении, исходящем из одного контекста, в других контекстах, и это приводит к философской путанице. Особенно это касается многозначных слов вроде "время", "сознание", "бытие". Ведь время в физике, время в истории, время в бытовом разговоре - это, на самом деле, совершенно разные вещи.

Французские философы середины XX века пошли ещё дальше Витгенштейна и пришли к выводу, что реальность не просто описывается языком, а реальность существует только внутри языка, и ничего вне языка нет вообще. Карта есть, а территории нет. Значение любого слова зависит от значений всех связанных с ним слов, и нет ни одного слова, независимого от других. Cмысл конкретного слова зависит от всего графа связей между всеми словами вообще.

Что такое квартира? Это выделенная часть дома. Что такое дом? Это отдельно стоящее здание. Что такое здание? Это жилое строение, обычно из камня или бетона. Что такое строение? Это архитектурная конструкция. И эту цепочку можно продолжать бесконечно.

Философ Жак Деррида описывал это словами "мир есть текст" - он утверждал, что знак не ведёт к вещи, он ведёт к другому знаку. Это отлично видно на примере внутреннего устройства современных больших языковых моделей. Позволю процитировать самого себя ещё раз:

Внутри больших языковых моделей и векторных баз данных понятия нашего мышления и слова нашего языка представлены в виде точек в тысячемерном пространстве смыслов. Каждое измерение этого пространства отвечает за определённый признак (feature) реальности. Человеческое визуальное воображение ограничено тремя измерениями, поэтому нам трудно визуально представить себе тысячемерное пространство. Мы не способны полноценно воспринимать даже четырёхмерное пространство — мы можем визуализировать лишь его трёхмерные срезы. Но несмотря на неспособность геометрического представления пространства смыслов, мы можем работать с точками в этом пространстве алгебраически.

Координаты точек семантически близких друг к другу понятий располагаются близко друг к другу: например точки понятий «огурец» и «помидор» ближе друг к другу, чем к точке понятия «молоток». Скопления близких друг к другу понятий образует определённые области смыслов: например, «огурец», «помидор» и «капуста» образуют вместе область пространства смыслов, центральная точка которого — понятие «овощи». В свою очередь маленькие области смыслов при объединении образуют более крупные: так области «овощи», «фрукты» и «ягоды» образуют вместе область, центральной точкой которого служит понятие «съедобные плоды». Можно думать об этом абстрагировании, как о своего рода вложенных множествах в теории множеств или иерархии классов в объектно‑ориентированном программировании.

Значения слов определяются лишь относительно других слов расстоянием до них в неком абстрактном пространстве смыслов - помидор ближе к огурцу, чем к молотку. Наше описание реальности, которое мы обычно и принимаем за реальность, зависит от структуры используемого нами языка - геометрического устройства этого самого пространства смыслов.

Ранний Витгенштейн был прав в том, что мир состоит из фактов, но это верно лишь для событий, которые мы можем считать внешней по отношению к нам объективной реальностью. Наш субъективный мир - это не факты, а интерпретации этих фактов. Если факты принять за точки, то интерпретации - это то, как мы соединяем эти точки в фигуры. Одни и те же точки можно соединить по-разному - любую историю можно рассказать тысячей способов. Каждый язык рассказывает историю по-своему - основываясь на одних и тех же фактах, марксист расскажет историю XX века одним способом, либерал - другим. Они будут использовать совершенно разные языки: марксист употреблять слова "класс" и "отчуждение труда", либерал - слова "рынок" и "эффективность". Продолжая метафору с картой и территорией, можно сказать, что у каждого путника в мире фактов своя карта, но ни одна из этих карт не полна.

Более того, в каждом символе на карте содержится свой смысл: у либерала слово "коммунист" несёт негативный окрас и находится близко к понятию "враг рода человеческого", а у коммуниста всё ровно наоборот. В мышлении средневекового крестьянина слово "ведьма" было связано с понятием "тёмные силы", темные силы связаны с дьяволом, дьявол - с Богом, а Бог - это серьёзно. В мышлении современного человека слово "ведьма" связано с образом из мультиков и с костюмами на Хеллоуин, то есть с чем-то несерьёзным. Слово одно и то же, но в разных системах имеет совершенно разные смыслы.

Если реальность разных групп людей зависит от используемого ими языка, то полностью объективная истина принципиально невозможна. Поэтому философия после второго лингвистического поворота стала заниматься исследованием символов, дискурсов и интерпретаций и их влияние на мышление людей. Ведь мышление зависит от системы отсчёта, заложенной в языке, прямо как порядок событий в общей теории относительности зависит от наблюдателя.

Продолжение во второй части.

Люди часто забывают или даже не задумываются о том, что многие обыденные вещи в окружающей нас сегодня действительности стали возможными лишь благодаря унификации технологического слоя, на котором эти вещи основаны. Существование бытовых приборов - микроволновок, телевизоров, стиральных машин, холодильников и компьютеров - было бы невозможно без повсеместного внедрения электричества, унификации напряжения в электрических сетях и унификации разъёмов розеток. Современная наука была бы невозможна без принятия единой математической нотации и одинаковых единиц измерения, а современный интернет - без повсеместного распространения компьютеров и унификации протокола обмена данными.

Одну из таких унификационных революций произвёл в середине XX века Малкольм Маклин - американский предприниматель, внедривший в индустрию грузоперевозок единый стандарт контейнеров. До контейнерной революции Маклина трюмы и палубы кораблей заполнялись товарами разной формы - доски, мешки, коробки и бочки с жидкостями загружались на борт вперемешку. Разная форма не позволяла заполнить доступный объём оптимальным способом. При необходимости довести товар от порта до места назначения требовалось перегрузить его в вагон поезда или кузов грузовика. Это всё было жутко долго и неудобно. Контейнеры изменили ситуацию.

Суть контейнерной революции состояла в абстракции процесса перевозки от перевозимого товара. Товары загружались в стандартизированные контейнеры определённой формы и объёма, а корабли, поезда и грузовики переделывались в платформы для перевозки этих самых стандартных контейнеров. Вся портовая и вокзальная инфраструктура была постепенно перестроена под массовое хранение, загрузку и разгрузку стандартизированных контейнеров. Благодаря этому процесс загрузки и выгрузки заметно ускорился, а после и вовсе автоматизировался.

В дальнейшем подобная контейнерная революция произошла в доставке программного обеспечения. Если прежде программистам приходилось строить свои самодельные системы для доставки кода приложений на сервер и его запуска, то названный в честь портовых грузчиков Docker позволил оборачивать любую программу в стандартизированный контейнер и запускать его на сервере с помощью автоматизированных средств развёртывания вроде Kubernetes.

Идея абстрагирования системы доставки от того, что именно доставляется, принесла человечеству огромную пользу. Но мы извлекли из стандартных физических контейнеров ещё далеко не всю пользу. В этом эссе я хочу поразмышлять, как с помощью контейнеров и тотальной майнкрафтизации мы можем выйти на следующий технологический уровень развития цивилизации. Внедрение контейнеров в перевозки заняло несколько десятилетий и потребовало полной перестройки людских умов. Полноценная контейнеризация нашей цивилизации потребует ещё больших усилий, но её результаты превзойдут все наши самые смелые мечты...

Контейнеры сейчас

В грузоперевозках уже давно всё специально проектируется под контейнеры: огромные морские корабли-контейнеровозы, железнодорожные вагоны-платформы и автомобильные грузовые прицепы для перевозки контейнеров, краны для их подъёма и переноса. Есть даже специальные контейнеры-бочки для перевозки жидкостей. Но сегодня контейнеры используются не только в грузоперевозках, но ещё и в строительстве, энергетике, промышленности, торговле и медицине. В разных странах из контейнеров делают киоски с фастфудом, автобусные остановки, мини-магазины, мобильные медпункты, бытовки для вахтовиков, жилые модули, целые дома, аквапонные фермы, сауны, мобильные центры обработки данных, мобильные дизельные электростанции и трансформаторы и много другое.

В последнее время к контейнерам присматриваются военные, и это касается не только логистики. Существуют проекты сведения тяжёлых вооружений к форм-фактору контейнера - артиллерийских установок, радаров и пусковых установок ПВО. Согласно замыслам сумрачных военных инженерных гениев, это поможет отделить вооружения от их носителей - один и тот же артиллерийский контейнер или контейнер-радар можно установить и на корабль, и на гусеничное шасси, и на колёсное шасси, и на вагон поезда. Можно даже быстро переделать гражданский контейнеровоз под какой-никакой, но боеспособный военный корабль. Кроме того, из контейнеров можно делать казармы на военных базах.

Мир, основанный на контейнерах

Чтобы выйти на следующий уровень технического развития цивилизации нам нужно полностью изменить наше мышление и начать мыслить контейнерами не как железными коробками с товарами внутри, а как соединяющимися друг с другом модулями - этакими строительными лего-блоками с чётко стандартизированными интерфейсами. Из этих модульных блоков мы сможем, как в Майнкрафте, строить такие мегаструктуры, о которых сейчас не можем и мечтать. Кроме того, эти мегаструктуры можно будет строить и сносить невероятно быстро. Представьте, что за неделю в чистом поле можно возвести целый город из контейнеров с жилыми зданиями, энергетикой, офисами, больницами, магазинами, кафе, храмами и прочими удобствами, а через какое-то время при необходимости за пару недель полностью разобрать и увезти - больше не будет никаких заброшенных городов-призраков вроде Воркуты.

Если создать стандартизированные строительные блоки на основе контейнеров, можно строить контейнерные многоэтажки: лестницы, коридоры, туалеты, кухни, ванные, гостиные, спальни - это всё отдельные контейнеры. Захотел и заказал на маркетплейсе новую комнату в свой частный дом. Каждый больничный кабинет - отдельный контейнер, а сама больница - просто набор контейнеров-кабинетов. Точно то же самое можно сделать с офисами, магазинами и кафе. Даже дороги в городе можно делать на основе закопанных в землю контейнеров: верхняя поверхность контейнера - дорожное полотно, а внутри пространство для коммуникаций - водопровода, труб, электрических и интернет-кабелей.

Возможно пространство внутри каждого отдельного контейнера будет использовано не оптимально, но настройка всей инфраструктуры на работу с контейнерами и их быструю перевозку и развёртывание даст невероятные результаты. Каждый Docker-контейнер содержит в себе отдельную операционную систему - это не оптимально, но преимущества контейнеризации перевешивают этот минус. Можно будет при необходимости очень быстро "рефакторить" города под новые технологические цепочки, за недели перестраивая целые районы. Нам нужно будет перестроить всю инфраструктуру на контейнерную логику: многие заводы должны будут принимать на входе и выпускать на выходе готовые контейнеры. Миллионы железных контейнеров будут идти по конвеерам от завода к заводы как в игре Factorio. И тогда наступит светлое контейнерное будущее!

Я знаю — город будет!
Я знаю — саду  цвесть!
Когда такие люди
В стране в советской есть!

Больше интересных постов и видео про философию и математику вы можете найти в моём телеграм-канале.

В начале XVI века была издана книга английского юриста и философа Томаса Мора под названием "Утопия", в которой описывалась идеальная по мнению автора структура общества. Название этой книги стало именем нарицательным и дало имя всему жанру подобных трактатов. Книга Мора была далеко не первой: ещё за две тысячи лет до её выхода в свет древнегреческий философ Платон опубликовал трактат "Государство", в котором излагал свои взгляды на общественное устройство. Кто только не создавал своих утопий: например, Карл Маркс с его манифестом коммунизма и диктатурой пролетариата или Карл Поппер с его "Открытым обществом и его врагами". Почему бы не сделать этого и мне?

Китайский философ-даос Лао-Цзы писал, что когда нечто доходит до предела, оно обращается в свою полную противоположность. Из истории нам известно, что любые попытки воплощения различных утопий в жизнь всегда заканчиваются их полной противоположностью - тоталитарными антиутопиями. Поэтому в этом эссе я планирую описать не утопию, которая практически невозможна, а метаутопию - не то, как общество должно быть устроено, а то на основе чего оно должно быть зиждется и как развиваться. Метаутопия в отличие от утопии может быть применима в реальности и полезна для реального общества.

В основании этой метаутопии лежат два инструмента программирования - типизированный язык программирования и система контроля версий. Возьмём для примера в качестве языка программирования TypeScript, а в качестве системы контроля версий - Git. Сегодня на TypeScript пишут и веб-приложения, и мобильные приложения, и программы командной строки, и сервера для приложений. Почему бы не написать на нём государство?

Основания

Существует два основных подхода по созданию интерфейса взаимодействия между различными модулями системы - "сначала спецификация - потом код" и "сначала код - потом спецификация". Давайте посмотрим, чем они отличаются и какой работает лучше.

В подходе "сначала спецификация" сначала типами задаётся доменная область и интерфейсы взаимодействия между разными модулями системы, а после этого один модуль имплементирует этот интерфейс, а остальные при необходимости обращаются к нему через этот интерфейс. Прямо как мы это делаем в программировании внутри каждого из модулей. Под модулями я здесь имею в виду не папки внутри кодовой базы одной и той же программы, а отдельные друг от друга части системы - фронтенд, бекенд, база данных или отдельный микросервис. Пример такого подхода: пишется типизированная RPC-спецификация интерфейса взаимодействия клиент-сервер, а после бекенд имплементирует этот интерфейс, а фронтенд вызывает методы, указанные в интерфейсе. Или другой пример: пишется Prisma-спецификация модели данных, по которой кодогенератор создаёт миграции для базы данных и код ORM-методов для сервера.

В подходе "сначала код" в начале пишется код одного из модулей, а после этого основанный на средствах рефлексии языка программирования кодогенератор извлекает из этого кода типы и записывает их в спецификацию. Примером такого подхода служит Swagger: сначала пишется код бекенда, а после специальный кодогенератор извлекает из кода Swagger-спецификацию, которая становится интерфейсом для фронтенда. Другой пример: TypeORM, в которой модель данных описывается классами с аннотациями средствами ORM, а после по ним генерируются миграции к базе данных.

За свою долгую карьеру программиста я часто использовал оба подхода и убедился в превосходстве подхода "сначала спецификация - потом код" над подходом "сначала код - потом спецификация". Второй подход почти всегда работает хуже, так как средства рефлексии в языках программирования обычно имеют изъяны и плохо обрабатывают пограничные случаи. Кроме того, второй подход переворачивает логику проектирования система вверх ногами - не модуль имплементирует интерфейс, а модуль декларирует свой интерфейс. Первый же подход, где в основе лежит спецификация, а не код, лёг в основу метода разработки под названием DDD - domain-driven design - проектирование, ориентированное на предметной области. В DDD в начале мы описываем в виде типов все сущности, с которыми мы работаем, а после типизированными интерфейсами задаём как одни части системы взаимодействуют с другими, и только после этого приступаем к реализации проекта.

Похожая идея лежит в основе такого течения мысли как web3. Многие ошибочно полагают, что web3 - это исключительно про криптовалюты. На самом деле, web3 - это гораздо более масштабная, чем криптовалюты, идея. В эпоху web1 интернет был децентрализированным, а интернет-ресурсы представляли собой почти полностью статичные странички или форумы. В эпоху web2 интернет-ресурсы стали веб и мобильными приложениями - гораздо более динамичными и интерактивными, но беда в том, что за это мы заплатили централизацией интернета в руках нескольких крупных платформ, которые владеют всеми аккаунтами и данными и решают, что показывать, а что нет, а кого вообще лишить доступа. Основной идеей web3 было обратно децентрализовать интернет, но не утратить интерактивность и взаимодействие между ресурсами.

Онлайн платежи, подконтрольные в web2 двум крупным сервисам по выпуску карт Visa и Mastercard и нескольким большим сервисам обработки платежей вроде Stripe, в web3 заменяются децентрализованными криптовалютами. Аккаунты заменяются криптовалютными кошельками - подтверждением идентичности служит подпись специального сообщения приватным ключом. Программные интерфейсы заменяются типизированными смарт-контрактами на блокчейне, которые исполняются автоматически. Платформы заменяются протоколами, на которых работают эти самые смарт-контракты. Управление этим всем добром происходит с помощью DAO - распределённых корпораций, работающих на смарт контрактах. Этот дивный децентрализованный интернет web3 был построен и сейчас существует рядом со старым web2, который за счёт своей централизации всё-таки гораздо удобнее в использовании.

Основные принципы web3 - это децентрализация и отсутствие единого центра власти, полное владение собственной идентичностью (твой приватный ключ подтверждает, что ты - это ты), отсутствие разрешений на использование платформ, отсутствие бана и деплатформинга, отсутствие необходимости доверять контрагенту, ведь смарт-контракт исполнится в полном соответствии со своим кодом, и никто не может на это повлиять. Последняя особенность смарт-контрактов и стала лозунгом всего web3-движения: код - это закон. Именно на этом принципе и на DDD-подходе я развиваю свою идею программистской метаутопии.

Метаутопия

Любое государство по своей сути представляет собой систему обработки информации - потоки информации текут из одних частей государственной системы в другие и обратно. А что управляет потоками информации? Код. Сейчас этот управляющий государственной системой код записан в виде законов в юридических документах. В программистской метаутопии этот код будет записан на типизированном языке программирования.

Всё законодательство метаутопии должно быть выражено в виде кода на TypeScript, лежащего в публичном git-репозитории. Законы могут быть разделены по модулям кода: модуль уголовного права, модуль гражданского права, модуль семейного права и так далее. Типы в этом коде отображают аксиоматически определённые понятия: компания, армия, президент, человек, животное, гражданин, иностранец и тому подобные. Наследование типов отображает взаимоотношения между сущностями - ну например, президент, гражданин и иностранец наследуют человеку в случае объектно-ориентированного подхода либо же обладают компонентом "человек" в случае сущностно-компонентной системы (entity component system). Из моего опыта в разработке видеоигр сущностно-компонентный подход проявляет себя гораздо гибче в системах со сложными связями.

Интерфейсы со списком методов отображают контракты взаимодействия различных структур и органов государства друг с другом: например, объект типа "президент" может произвести объект типа "указ" и направить его в метод объекта "армия", которая внутри себя инкапсулирует сложную структуру - объект типа "генеральный штаб" вызывает методы объекта типа "батальон", и так далее. Таким образом, всё законодательство целиком, все формальные взаимодействия разных частей государственной машины полностью выражаются в виде типизированного программного кода. Это позволяет социальному архитектору видеть картину целиком.

Каждое изменение законодательства, каждый законопроект - это пулреквест, каждое кодревью и обсуждение пулреквеста - это по сути работа профильного комитета парламента. Проверка непротиворечивости законов друг другу осуществляется проверкой типов компилятором. Тестировщики пишут юнит-тесты для проверки того, что работа законов соответствует целям их принятия и интеграционные тесты для проверки взаимодействия разных законов друг с другом. Пентестеры проводят аудит законов и пытаются найти эксплойты в законодательстве, которые могли бы использовать злоумышленники. Статический анализ кода проверяет, что нельзя создать закон, который прямо дискриминирует конкретную группу населения.

Такая система будет полностью прозрачна для всех граждан, для всех организаций, для самого государства. Станет возможным гораздо проще проводить реформы - юридическая часть реформ будет представлять собой просто рефакторинг кода, после которого целостность новых законов будет проверяться компилятором и тестами. Государственные и частные организации должны быть обязаны полностью в виде API имплементировать свои интерфейсы. Конечно, наложение этих типизированных интерфейсов на реальные организации - это сложнейшая задача, которой прошлая структура будут сильно сопротивляться, но эволюционным путём за десятки лет это преобразование произвести возможно. Электронные госуслуги со скрипом и треском внедрялись в государствах в течении многих лет, но в конце концов были успешно внедрены.

Конечно, как и любая другая утопия, при реальной имплементации в жизнь эта метаутопия программистов-аутистов может привести к ужасным антиутопическим последствиям. И, скорее всего, обязательно приведёт. Но я верю, что государства XXII века будут похожи именно на такие структуры - state as code.

Больше интересных постов и видео про философию и математику вы можете найти в моём телеграм-канале.

Продолжение первой части.

Время

Пример, приведённый для доказательства отсутствия субстанциональности пространства работает и для времени. Представьте себе мир, в котором находится множество различных объектов, но не происходит никаких изменений. Сможет ли наблюдатель утверждать существование в таком мире времени? Конечно же, нет. Время возможно заметить и измерить только, если что-то изменяется. Мы измеряем течение времени ритмами изменений - восходами и заходами солнца, изменениями положения солнца на небосводе и так далее.

Связь между временем и событиями в нём точно такая же как между пространством и объектами, идеями и материей - время определяется происходящими в нём изменениями, а сами эти изменения могут быть восприняты лишь внутри временного потока. Одно без другого существовать не может.

Все мы знаем строки из советской песни:

Есть только миг между прошлым и будущим - именно он называется жизнь

Похожим образом Нагарджуна критиковал субстанциональность времени. Согласно его рассуждениям, прошлое и будущее не существует в онтологическом значении этого слова. Прошлое - это воспоминания у нас в голове, иногда неточные, иногда даже ложные. Будущее - это надежды и планы у нас в голове. Ни того, ни другого кроме как у нас в уме не существует. А что тогда такое настоящее? Краткий миг между прошлым и будущим? Как может обладать независимым субстанциональным существованием что-то, что определяется как точка между двумя несубстанциональными сущностями? Даже если предположить, что прошлое существовало и будущее будет существовать, то настоящее всё ещё будет моментом между тем, чего уже нет, и тем, чего ещё нет. Как две сущности, которых нет, могут определять что-то, что есть? Никак.

Таким образом, время - тоже не субстанция. Прошлое, настоящее и будущее существуют лишь относительно друг друга. Да и то, согласно теории относительности, порядок событий во времени субъективен для каждого наблюдателя.

Движение

Критика субстанциональности движения вытекает из объединения отсутствия субстанциональности у пространства и времени. В своём трактате "Коренные строфы о срединности" Нагарджуна приводит аргумент, напоминающий апорию Зенона о стреле. Вполне вероятно, что Нагарджуна был отдалённо знаком с греческой философией, так как жил в культурной среде, созданной греко-буддизмом. Его метод критики прасанга напоминает метод критики древнегреческой школы скептицизма Пиррона, который в свою очередь, будучи придворным философом Александра, почерпнул многие из своих убеждений у буддийских философов во время индийского похода Александра.

Апория Зенона о стреле звучит так:

Летящая стрела неподвижна, так как в каждый момент она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

Награджуна же говорит следующее. То, что уже прошло путь, не движется. То, что ещё не прошло, тоже не движется. Кроме "прошедшего" и "не-прошедшего" — где движение? Его нет. Но может быть движение заключено в том, что движется? Но если движение заключено в движущемся, то движение может либо быть тождественно движущемуся, либо быть отличным от него. Если оно тождественно движущемуся, то получается абсурд - бег не может быть тождественен бегуну - это категориальная ошибка. Если же это разные вещи, то получается, что движение возможно без движущегося, а движущееся без движения. Это кажется просто словоблудием - о чём вообще говорит этот безумный философ?

Важно помнить, что цель Нагарджуны - не играть в слова, а доказать, что ни движение, ни движущаяся сущность не могут обладать независимой субстанциональной природой. Движение и движущееся - это просто название разных частей графа реальности, той самой сети драгоценных камней Индры из приведённой мною сутры. Они существуют только лишь относительно друг друга, но не сами по себе.

Следующий шаг в рассуждении Нагарджуны заводит его гораздо дальше Зенона - он утверждает, что раз нет движения как субстанции, то нет как субстанции и покоя. Нагарджуна хочет сказать, что находясь в зеркальном лабиринте отражений, мы пытаемся схватить эти отражения рукой, так как нам кажется, что они есть, а их на самом деле в онтологическом смысле нет, хотя вот же они прямо перед нами.

Причинность

В своём трактате о срединности Нагарджуна ныряет в глубины одной из самых сложных областей философии - метафизику причинности. Его интересует вопрос о субстанциональности причинно-следственных связей, в число которых входят, например, законы физики. Вопрос о том, как вообще причины порождают следствия, кажется предельно глупым, но чем больше о нём задумываешься, тем сложнее он становится. Почему законы физики вообще работают? Что принуждает материю подчиняться им? Если мы мыслим в парадигме субстанций, ответа на этот вопрос мы найти не сможем.

Первым делом стоит заметить, что в мире всё находится в постоянном движении, и всё, что мы представляем себе как статичные вещи - это, на самом деле, просто кратковременная стабильность динамических процессов. Британский философ Алан Уотс любил демонстрировать этот факт на примере кулака. То, что мы называем существительным "кулак" мыслится нами как статичная вещь, так как существительными мы называем статичные вещи, но стоит его разжать в открытую ладонь, и кулак исчезает. Как может вещь просто исчезнуть за секунду? Тут нам становится очевидным, что мы посчитали кратковременную стабильность движения нашей руки за статичную сущность. Таким же образом мы можем проанализировать любую другую вещь - дом, человека, государство, и окажется, что эта вещь - лишь кратковременная стабильность динамических процессов. Поэтому мир состоит не из вещей, а из событий.

Нагарджуна показывает, что события не могут существовать субстанционально сами по себе. Если событие случилось, то что служит его причиной? Причина появления события не может заключаться в нем самом, так как если оно уже есть, то ему не нужно появляться. Если причина в другом независимо существующем событии, то между этими двумя событиями нет никакой связи - что угодно могло бы появляться из чего угодно. Может быть у событий вообще нет причин - но тогда мир был бы абсолютно случайным, а мы наблюдаем, что это не так. Значит события не обладают независимой природой, а служат просто именами - инструментами нашего ума по обозначению узлов в сети отношений. Но может субстанциональностью обладают сами причинно-следственные связи?

Следствие всегда темпорально следует за причиной, потому оно и называется следствием. Когда событие-следствие есть, события-причины уже нет - оно в несуществующем уже прошлом. Когда событие-причина ещё есть, события следствия ещё нет - оно в несуществующем ещё будущем. Причина и следствие никогда не существуют одновременно, как тогда одно может порождать другое?

Философский метод Нагарджуны кажется очень странным, непривычным и малопонятным западному читателю. Поэтому я ещё раз упомяну, что его цель - довести до абсурда утверждения о независимой природе субстанций. Причины и следствия очевидно существуют, но только-лишь как взаимосвязанные части единого процесса проистекания реальности.

Причинно-следственные связи, как и законы физики - это инструменты мышления по анализу этого процесса, но сами по себе они не существуют - только как взаимное отражение великого гиперграфа, описанного в моём переводе "Стивен Вольфрам: кажется, мы близки к пониманию фундаментальной теории физики, и она прекрасна". Материи не нужно подчиняться каким-то записанным Богом в книге бытия математическим формулам, ведь эти формулы - это просто описание взаимосвязей событий друг с другом, но при этом события чётко следуют этим формулам. Эта мысль кажется противоречивой и безумной, и так оно и есть. Отражение и то, что отражается, движется полностью синхронно. Об этом повествует мой любимый коан "Лис Хякудзё" из "Бездверной двери":

Как-то, когда Хякудзё читал монахам наставления по дзэн, там присутствовал один старик, невидимый монахам. По окончании наставлений, когда монахи расходились, уходил и он. Но однажды после их ухода он остался, и Хякудзё спросил его: «Кто ты?»

Старик ответил: «Я не человек, но был им, когда Будда Кашьяпа проповедовал в этом мире. Я был мастером дзэн и проповедовал на этой горе. Один из моих учеников спросил меня тогда, подчинён ли просветлённый закону причинности Я ответил ему: «Просветлённый не подчиняется закону причинности». За этот ответ, свидетельствующий о моей приверженности безусловному, я на пятьсот рождений стал лисом и всё ещё пребываю им. Может быть, вы избавите меня от этого состояния своими словами дзэн и поможете оставить тело лиса? Можно мне спросить вас, подчиняется ли просветлённый закону причинности?»

Хякудзё сказал: «Просветлённый един с законом причинности». При этих словах Хякудзё старик обрёл просветление. «Я освободился, — сказал он, благодаря почтительным поклоном учителя. — Я больше не лис и должен оставить тело в своём жилье за этой горой. Прошу вас похоронить меня как монаха».

На следующий день Хякудзё через старшего монаха передал всем наказ приготовиться к похоронам монаха. «Но в лазарете нет ни одного больного, — удивились монахи, — о ком же говорит учитель?» После обеда Хякудзё вывел монахов со двора и повёл их за гору. Там он своим посохом вытащил из пещеры труп старого лиса и произвёл церемонию кремации. Вечером, беседуя с монахами, Хякудзё рассказал им эту историю о законе причинности.

Выслушав рассказ, Обаку сказал Хякудзё: «Я понял, что очень давно один человек дал неверный ответ о дзэн и из-за этого стал на пятьсот рождений лисом. Теперь я хочу спросить: если в наше время мастеру задают много вопросов, и он всегда отвечает верно — что станет с ним?»
— Подойди-ка поближе, я тебе отвечу, — сказал Хякудзё. Обаку подошёл к учителю, и тот отвесил ему оплеуху — он знал, что именно этот ответ и собирался дать учитель ему. От такой проницательности Хякудзё хлопнул в ладоши и рассмеялся. «Я думал, что у персов красные бороды, — сказал он, — а теперь я знаю перса с красной бородой».

Количество

Рассмотрение Нагарджуной онтологической реальности количества похоже на его рассмотрение реальности платоновских идей. Представьте себе, что перед вами на столе лежит три яблока, три апельсина и три вишни. Апельсины, яблоки и вишни не похожи друг на друга, это разные виды фруктов и ягод, но ум выделяет в них нечто общее - их количество. Число три - это платоническая идея, а они, как мы уже доказали, не субстанциональны. Но может быть число чем-то отличается? Давайте проверим.

Количество и считаемые вещи находятся в тех же самых отношениях как идеи и материя, пространство и объекты, время и события - мы никогда не встречаем количество, не воплощённое в множественности вещей. Конечно, мы можем оперировать с числами как с чистыми идеями математически, но представить себе значение числа три без считаемых вещей мы не можем. Тут Нагарджуна использует интересную аргументацию.

Множественность вещей существует лишь как совокупность единиц - три это один плюс один плюс один. То есть множественность по логике мереологического нигилизма не обладает независимым существованием, так как состоит из составных частей. Но единица тоже существует только при существовании множества - если было бы только неделимое единое, то мы бы ничего не могли различить, а значит и посчитать.

Если есть субстанциональная единичность, то эта единичность не может быть делима, ведь если у неё есть части, то это уже не единичность, а множественность. Но если она едина, то нет ничего, относительно чего мы могли бы что-то различить и посчитать. Нельзя сказать, что вещей много, а значит есть количество, так как чтобы посчитать вещи, они уже должны быть различимы. Поэтому количество — это просто удобная метка, инструмент ума, а не часть реальности. Единственность и множественность существуют лишь относительно друг друга, а не как независимая сущность реальности.

В поисках света

Когда фокусник показывает нам своё мастерство, наблюдаемая нами магия удивляет и радует нас. Но если мы знаем секрет фокуса, ощущение волшебства пропадает. Помните, как в детстве новогодние праздники с Дедом Морозом и подарками под ёлкой казались нам временем абсолютного волшебства? А теперь когда мы уже взрослые и это волшебство организуют не наши родители, а мы сами, волшебство исчезло. Понимание механизма работы убивает волшебство.

В исчезновении из жизни волшебства состоит главная трагедия человека эпохи постмодерна. Мы уже не верим в Бога, так как разумом, логикой и философией разложили все религиозные идеи и саму религию на составные части и системы. Например, ад не пугает нас, так как мы разумом понимаем, что идея наказания за наши поступки - это мем, который присутствует в каждой религии, потому что он помогает этой религии выживать, мотивируя людей принимать и распространять идеи этой религии из-за страха перед наказанием. Мы же ежедневно наблюдаем как тем же самым механизмом пользуются различные секты скорого конца света и телефонные мошенники. Но узнав и поняв механизмы работы этих конструктов, мы потеряли то волшебство, что было в религиях и идее Бога. Серость постепенно захватила наш мир, полностью выдавив из него волшебство.

Как мы можем во что-то верить, если знаем, что ни у этики, ни у математики, ни у познания нет никаких твёрдых оснований? Нет абсолюта, нет абсолютных истин, нет ничего субстанционального, одна сплошная пустота. Ум пытается найти смысл, найти основания, и не находя их, страдает от бессмысленности всего сущего. Нам безумно хочется погреться лучами яркого божественного света, озаряющего нашу душу спокойствием и радостью, но, к сожалению, мы утратили веру в существование этого света. Человек эпохи постмодерна не может избавиться от мысли, что свет - это просто иллюзия, его собственная придумка, а Бог - просто конструкт в его голове. Так эту боль описывал американский психолог Ирвин Ялом:

Нам по природе свойственно искать смысл. И нам приходится считаться с тем неудобным фактом, что нас забросили во вселенную, которая изначально бессмысленна. И поэтому, чтобы избежать отрицания всего и вся, мы вынуждены брать на себя сразу две задачи. Сначала - придумать или найти дело, в котором для нас будет заключаться смысл жизни, - достаточно жизнеспособное, чтобы нам его хватило на всю жизнь. А потом мы должны умудриться заставить себя забыть о том, что его придумали, и внушить себе, что это дело - совсем и не наше изобретение, что оно существует независимо от нас, где-то там, а мы его просто обнаружили.

Если нет финального ответа, нет абсолюта, нет "чего-то, что в итоге есть", то как это может вести к свету, а не к экзистенциальному мраку? Ответ Нагарджуны необычен, но глубок - страдание порождается не отсутствием основания, а желанием его иметь. Ключевой вопрос буддийской философии состоит не в том, что реально, а что нет, а в том, где и как возникает страдание. Возьмём, например, любую этическую систему, которые, как мы уже разбирали ранее, строятся на метафизических утверждениях о ценностях. Если мы привязываемся к этой этической системе, то в точках, где сущее расходится с должным, мы чувствуем несправедливость и начинаем страдать. Поэтому единственный способ не страдать - отказаться от привязанностей к любым метафизическим системам.

Учение о пустоте Нагарджуны - это не новая онтология, она отрицает любые субстанции, незыблемые основания и даже свой собственный статус как истины. Нагарджуна прямо утверждал, что тот, кто делает из самой пустоты воззрение, неисцелим. По его словам, "пустота сама пуста". С его точки зрения, любое метафизическое утверждение - это привязанность, а привязанность - источник страдания. Если Людвиг Витгенштейн и другие позитивисты отказываются от метафизики, потому что о том, о чём нельзя говорить осмысленно, следует молчать, то Нагарджуна и его последователи отказываются от метафизики потому, что пока ты хочешь говорить о реальности или существовании чего-либо, ты ещё не свободен. А чтобы освободиться, нужно отпустить все воззрения, отказаться от всех метафизических утверждений.

С точки зрения буддизма, философия и рассуждения про реальность или нереальность чего-либо представляют собой когнитивный онанизм, доставляющий человеку умственное удовольствие, но абсолютно бессмысленный и даже вредный для психического здоровья. За шесть веков до Нагарджуны сам Будда пытался донести эту мысль с помощью знаменитой притчи об отравленной стреле:

Один человек был поражён отравленной стрелой. Тогда его друзья и родственники призвали сведущего врача. Что, если бы больной в этом случае сказал: «Я не позволю лечить рану, пока не узнаю, кто тот человек, как его имя, какого он роду-племени, из какого оружия была выпущена стрела»? Каков был бы конец всего этого? Человек, скорее всего, умер бы. Жизнь коротка, энергия ограничена. Не стоит отвлекаться на вопросы, которые не ведут к пробуждению.

Сказать, что такое просветление (пробуждение, освобождение) трудно, так как любое описание превращает просветление в объект, а просветление - это крах субъект-объектного деления. Будда не описывал просветление как переживание субъекта, так как при просветлении сама идея устойчивого субъекта растворяется. А Нагарджуна пришёл к кажущемуся парадоксальным утверждению: нет того, кто может быть освобождён - и именно поэтому освобождение вообще возможно. Оно просто ощущается как отсутствие того, кто должен что-то ощущать.

Обрушение повседневного ума

Разные направления буддизма предлагают разные методы достижения освобождения. Большинство предлагает долгие годы изучать буддийские философские трактаты. После многих лет изучения философии и медитаций ум ученика избавляется от десятков иллюзий о субстанциональности "Я", времени, пространства, квалиа, внешнего мира, идей и в итоге в один прекрасный момент переходит из состояния неведения в состояние просветления.

В дзен-буддизме долгое изучение философии считают излишним, а сутры в монастырях обычно хранят рядом с отхожим местом, показывая тем самым своё к ним отношение. В японской школе дзэн Риндзай считается, что можно обойтись без долгой подготовки к фазовому переходу ума из состояния неведения в состояние просветления и обрушить ум единомоментно. Делают это они с помощью коанов - алогичных загадок, которые ученик должен разгадать, и ответом на которые служат не слова, а действие. Самый известный из коанов - "как звучит хлопок одной ладони?". Логического ответа на коан не существует, все возможные логические ответы можно разрушить прасангой. Эта алогичность зацикливает ум ученика, и в один момент какое-то случайное событие в его жизни приводит к мгновенному озарению и обрушению старого ума.

Метод достижения просветления, описанный Боддхидхармой, одним из первых патриархов дзен-буддизма, заключался в том, чтобы указать уму на самого себя и тем самым обрушить его из повседневного состояния в просветлённое. Этот метод чем-то похож на метод доказательства австрийским математиком Куртом Гёделем его знаменитых теорем о неполноте - создать на языке формальной системы высказывание, указывающее на само себя. Мастерски это обрушение сознание методом дзен описал в своём романе "Чапаев и пустота" Виктор Пелевин:

- А вот вы скажите, Василий Иванович, только как на духу. Вы красный или белый?- Я? - спросил Чапаев, переводя на меня взгляд. - Сказать?
Он взял со стола две луковицы и принялся молча чистить их. Одну он ободрал до белизны, а со второй снял только верхний слой шелухи, обнажив красно-фиолетовую кожицу.
- Гляди, Петька, - сказал он, кладя их на стол перед собой. - Вот перед тобой две луковицы. Одна белая, а другая красная.
- Ну, - сказал я.
- Посмотри на белую.
- Посмотрел.
- А теперь на красную.
- И чего?
- А теперь на обе.
- Смотрю, - сказал я.
- Так какой ты сам - красный или белый?
- Я? То есть как?
- Когда ты на красную луковицу смотришь, ты красным становишься?
- Нет.
- А когда на белую, становишься белым?
- Нет, - сказал я, - не становлюсь.
- Идем дальше, - сказал Чапаев. - Бывают карты местности. А этот стол - упрощенная карта сознания. Вот красные. А вот белые. Но разве оттого, что мы сознаем красных и белых, мы приобретаем цвета? И что это в нас, что может приобрести их?
- Во вы загнули, Василий Иванович. Значит, ни красные, ни белые. А кто тогда мы?- Ты, Петька, прежде чем о сложных вещах говорить, разберись с простыми. Ведь "мы" - это сложнее, чем "я", правда?
- Правда, - сказал я.- Что ты называешь "я"?
- Видимо, себя.
- Ты можешь мне сказать, кто ты?
- Петр Пустота.
- Это твое имя. А кто тот, кто это имя носит?
- Ну, - сказал я, - можно сказать, что я - это психическая личность. Совокупность привычек, опыта... Ну знаний там, вкусов.
- Чьи же это привычки, Петька? - проникновенно спросил Чапаев.
- Мои, - пожал я плечами.
- Так ты ж только что сказал, Петька, что ты и есть совокупность привычек. Раз эти привычки твои, то выходит, что это привычки совокупности привычек?
- Звучит забавно, - сказал я, - но, в сущности, так и есть.
- А какие привычки бывают у привычек?
Я почувствовал раздражение.
- Весь этот разговор довольно примитивен. Мы ведь начали с того, кто я по своей природе. Если угодно, я полагаю себя... Ну скажем, монадой. В терминах Лейбница.
- А кто тогда тот, кто полагает себя этой мандой?
- Монада и полагает, - ответил я, твердо решив держать себя в руках.
- Хорошо, - сказал Чапаев, хитро прищуриваясь, - насчет "кто" мы потом поговорим. А сейчас, друг милый, давай с "где" разберемся. Скажи-ка мне, где эта манда живет?
- В моем сознании.
- А сознание твое где?
- Вот здесь, - сказал я, постучав себя по голове.
- А голова твоя где?
- На плечах.
- А плечи где?
- В комнате.
- А где комната?
- В доме.
- А дом?
- В России.
- А Россия где?
- В беде, Василий Иванович.
- Ты это брось, - прикрикнул он строго. - Шутить будешь, когда командир прикажет. Говори.
- Ну как где. На Земле.
- А Земля где?
- Во Вселенной.
- А Вселенная где?
Я секунду подумал.
- Сама в себе.
- А где эта сама в себе?
- В моем сознании.
- Так что же, Петька, выходит, твое сознание - в твоем сознании?
- Выходит так.
- Так, - сказал Чапаев и расправил усы. - А теперь слушай меня внимательно. В каком оно находится месте?
- Не понимаю, Василий Иванович. Понятие места и есть одна из категорий сознания, так что...
- Где это место? В каком месте находится понятие места?
- Ну, скажем, это вовсе не место. Можно сказать, что это ре...Я осекся. Да, подумал я, вот куда он клонит. Если я воспользуюсь словом "реальность", он снова сведет все к моим мыслям. А потом спросит, где они находятся. Я скажу, что у меня в голове, и... Гамбит. Можно, конечно, пуститься в цитаты, но ведь любая из систем, на которые я могу сослаться, подумал вдруг я с удивлением, или обходит эту смысловую брешь стороной, или затыкает ее парой сомнительных латинизмов. Да, Чапаев совсем не прост. Конечно, есть беспроигрышный путь завершить любой спор, классифицировав собеседника, - ничего не стоит заявить, что все, к чему он клонит, прекрасно известно, называется так-то и так-то, а человеческая мысль уже давно ушла вперед. Но мне стыдно было уподобляться самодовольной курсистке, в промежутке между пистонами немного полиставшей философский учебник. Да и к тому же не я ли сам говорил недавно Бердяеву, заведшему пьяный разговор о греческих корнях русского коммунизма, что философию правильнее было бы называть софоложеством?
Чапаев хмыкнул.
- А куда это вперед может уйти человеческая мысль? - спросил он.
- А? - растерянно сказал я.
- Вперед чего? Где это "впереди"? Я решил, что по рассеянности заговорил вслух.
- Давайте, Василий Иванович, по трезвянке поговорим. Я же не философ. Лучше выпьем.
- Был бы ты философ, - сказал Чапаев, - я б тебя выше, чем навоз в конюшне чистить, не поставил бы. А ты у меня эскадроном командуешь.

***

- Знаете, Василий Иванович, не идут у меня из головы ваши слова. Умеете вы в тупик загнать.
- Верно, - сказал Чапаев, с силой проводя щеткой по спутанным конским волосам, - умею. А потом как дать из пулемета...
- Но мне кажется, - сказал я, - что я и могу.
- Попробуй.
- Хорошо, - сказал я. - Я тоже задам последовательность вопросов о местоположении.
- Задавай, задавай, - пробормотал Чапаев.
- Начнем по порядку. Вот вы расчесываете лошадь. А где находится эта лошадь?
Чапаев посмотрел на меня с изумлением.
- Ты что, Петька, совсем охренел?
- Прошу прощения?
- Вот она.
Несколько секунд я молчал. К такому повороту я совершенно не был готов. Чапаев недоверчиво покачал головой.
- Знаешь, Петька, - сказал он, - шел бы ты лучше спать.

Виктор Пелевин, "Чапаев и Пустота"

Заключение

Таким образом, в мире нет ничего субстанционального, ничего существующего абсолютно независимо. Всё взаимно зависит от чего-то другого. И это знание помогает нам обрушить наш повседневный ум и пробудиться...

Больше интересных постов и видео про философию и математику вы можете найти в моём телеграм-канале.

Наше мышление целиком и полностью определяется нашим повседневным опытом и необходимостью действовать в окружающем нас обыденном мире. Поэтому, когда мы сталкиваемся с вопросами, выходящими далеко за пределы нашего повседневного опыта, наше мышление начинает давать сбои и приводит нас к неправильным ответам. Людям с трудом даются такие далекие от бытовых представлений о реальности области науки как теория вероятности, теория относительности и квантовая механика. А та картина мира, которую рисуют эти теории, кажется нам глубоко контринтуитивной и противоречащей здравому смыслу. Одно из таких ложных представлений о реальности я как раз и хочу разобрать в этом посте - вопрос о существовании таких субстанций как пространство, время, материя и сознание.

Субстанция и пустота

Всю историю философии одним из основных её направлений была онтология - дисциплина, пытающаяся ответить на вопрос "Что существует?" и на метавопрос "Что такое существовать?". Классическая онтология с древних времён понимала свою задачу как поиск субстанции - чего-то, что, по определению французского философа Рене Декарта, не нуждается в чём-то другом, чтобы существовать. Материалисты, вроде Левкиппа и Демокрита, считали субстанцией атомы - неделимые частицы материи, объективные идеалисты, вроде Пифагора и Платона, считали субстанцией вечные идеи вроде математических равенств и геометрических фигур, субъективные идеалисты вроде Шанкары, Бёркли и Фихте, считали субстанцией сознание. Важно понимать, что все эти воззрения основаны на метафизических утверждениях. А что такое метафизика?

Метафизика находится за пределами физики. Физика - это то, что описывает языком математики наблюдаемые в окружающем мире отношения между объектами, метафизика же - это философские утверждения о природе этих объектов. Физика - это территория знания, метафизика - это территория веры. На территории знания работает научный метод - мы можем поставить эксперимент и проверить, что отношения между объектами и описывающие их законы действительно таковы, какими их предполагают наши теории. Но не существует даже теоретической возможности поставить эксперимент, который бы доказал или опроверг фундаментальность сознания или материи - а значит, согласно принципу фальсифицируемости, определённому философом науки Карлом Поппером в качестве критерия научности, любые метафизические утверждения выходят за пределы возможностей научного метода.

Любые этические системы основаны на метафизических провозглашениях высших ценностей. Поэтому никакая этическая система, как это заметил шотландский философ Дэвид Юм, не может быть выведена из физики - "как оно должно быть" не выводимо из "как оно есть". Права человека не выводятся из уравнений квантовой механики. Если кто-то утверждает, что, например, согласно научным исследованиям какое-то действие снижает детскую смертность, а значит это действие хорошее, то он в своих рассуждениях неявно опирается на подразумеваемое метафизическое утверждение "детские жизни ценны". Более подробно я разбирал этику в своём эссе "Как Фёдор Михайлович Достоевский и Фридрих Ницше повлияли на мировоззрение Дарта Вейдера".

Количество возможных метафизических аксиоматик бесконечно велико, и из каждой такой аксиоматики выводится своя картина мира подобно тому, как в математике из каждой аксиоматики выводится своя уникальная система. Например, в человеческом обществе существует огромное количество различных этических систем, опирающихся на различные метафизические утверждения, которые часто в определённых точках вступают друг с другом в противоречие и приводят к ожесточённым спорам - примером тому может служить вопрос допустимости абортов. Утверждения о субстанциональности, то есть независимом существовании, материи, сознания или абстрактных идей тоже порождают свои картины мира - материализм, объективный и субъективный идеализм и многие другие. Все они неверны? Или какая-то из них верна?

Ответ на эти вопрос предложил буддийский философ Нагарджуна, и этот ответ - радикальный отказ от метафизики. В своём магнум опусе "Коренные строфы о срединности" Нагарджуна доказывает противоречивость всех метафизических систем и отрицает субстанциональность каких-то ни было объектов. Выведенное им учение о пустотности может считаться одной из первых апофатических критических теорий - он предложил критику и деконструкцию других теорий без выдвижения каких-либо конструктивных утверждений. В учении о пустотности Нагарджуна не опровергает существование вещей: он не говорит, что материи, пространства, времени, идеи круга или красного цвета не существует - он утверждает, что все эти вещи существуют, но не обладают самобытиём, субстанциональностью, независимым от чего-то другого существованием. В своём трактате Нагарджуна доказывает утверждение своего духовного наставника Будды о взаимозависимости всех вещей.

Используемый Нагарджуной философский метод прасанги - это не выдвижение собственной доктрины, а доведение чужой позиции до логического обрушения. Это напоминает популярный в западной философии приём reductio ad absurdum - доведение до абсурда. Буддизм часто обвиняют в нигилизме - утверждении того, что ничто по-настоящему не существует и ничто не истинно. Но на самом деле, буддизм столь же далёк от нигилизма, как и от этернализма - утверждения о существовании какой-либо вечной субстанции. Нагарджуна не утверждает существование вещей, но и не отрицает его - даже само название его трактата "Коренные строфы о срединности" говорит о том, что его метод - придерживаться указанного Буддой срединного пути между крайностями. Созданное Нагарджуной учение о срединном пути, называемое мадхьямикой, проводит разделение между двумя уровнями истины: на уровне относительной, конвенциональной истины вещи существуют, но на уровне абсолютной, предельной истины вещи не обладают самобытиём. Когда вы едите суп, ложка есть, когда вы задумываетесь о её бытии, ложки нет.

По легенде, Нагарджуна пришёл к просветлению и своему учению о пустотности во сне. Ему приснилась ступа - буддийское ритуальное строение для хранения праха Будды или свитков с сутрами. Разрушив её, он обнаружил внутри точно такую же ступу поменьше. Он разрушил и её, но внутри обнаружил только ещё одну такую же ступу. Нагарджуна разрушал эти ступы‑матрёшки одну за другой, пытаясь найти, что лежит в их основе, но в один момент осознал, что ступы бесконечно вложены друг в друга и тут же пробудился. Монах понял, что никакого содержания у вещей нет, нет никакой субстанции, из которых всё состоит,  всё, что есть — это лишь взаимозависимое возникновение одних вещей относительно других.

Давайте посмотрим, как Награджуна критикует субстанциональность и раскрывает взаимозависимость различных объектов - идей, материи, сознания, пространства, времени и других.

Идеи

Древнегреческий философ Платон оставил нам, своим потомкам, учение о вечных идеях. Его занимал вопрос о том, где и в каком виде существуют математические истины - такие, как, например, число Пи. Какой бы народ в мире не пришёл к созданию геометрии, длина окружности их круга будет всегда относиться к его диаметру как Пи к одному. Даже если мы вступим в контакт с инопланетянами из другой галактики, число Пи у них будет таким же, как и у нас, а дважды два будет равно четырём, а следовательно математика независима от пространства. Кроме того, число Пи было таким же, как и сейчас, миллион лет назад и будет таким же через миллион лет после нашей смерти, а значит, математика независима и от времени. Платон демонстрировал независимость идей от человека на примере пяти правильных многогранников, в честь него позже названных платоновыми телами: существует всего пять правильных многогранников и древние греки строго доказали, что шестого быть не может, а следовательно математика - не есть продукт деятельности человека и даже богов, ведь создать шестой невозможно логически. Следовательно, эти вечные и независимые идеи существуют сами по себе в некоем особенном "пространстве", которое Платон называл миром идей.

Материальный мир Платон считал блёклой тенью мира идей. В рассказанном им мифе о пещере люди представлены в виде узников, прикованных к стене пещеры - за их спинами светит огонь, откидывающий на стену пещеры тени проносимых мимо него предметов. Узники принимают эти тени на стене за реальность, хотя на самом деле реальны лишь откидывающие тени предметы. Этой метафорой Платон хотел показать, что материальные предметы - это иллюзорные тени единственно реальных идей. Так, например, материальное колесо - это тень идеального круга.

Кроме математических истин в мире идей содержатся так называемые универсалии - абстракции, объединяющие предметы в единую категорию. Предположим, у вас дома живёт три кошки разных пород и цветов - одна рыжая, другая чёрная, третья белая. Что позволяет смести их всех под одну гребёнку, подвести под одну абстрактную категорию "кошка"? Эта трудноопределимый набор признаков, который делают кошку кошкой и отличает её от собаки - некая "кошкость". Эта самая кошкость и есть универсалия. С древних времён философы спорят реальны ли универсалии или реальны только отдельные кошки, а универсалии - лишь объект в нашем мышлении. Этот вопрос я подробно разбирал в эссе "Nomina nuda tenemus: открываем ли мы математические законы или просто придумываем их?".

На этот вопрос существует несколько разных ответов. Сам Платон считал идею кошкости реальной. Его ученик Аристотель считал, что идеальные формы могут проявляться лишь воплощаясь в материи - грубо говоря, идея кошки, кошкость, существует лишь воплощённая в конкретных материальных кошках. Фома Аквинский утверждал, что идеи и формы существуют в трёх видах: в абстрактном виде в мире идей, в воплощённом в материи виде в материальном мире, в виде мыслей в нашем мышлении - абстрактные идеи воплощаются в материи, а мы смотря на материальные предметы познаём эти абстрактные идеи в нашем мышлении. Вопрос о соотношении идей и материи выразился в знаменитом парадоксе корабля Тесея:

Согласно легенде, дошедшей до нас благодаря Плутарху, корабль, на котором мифологический герой Тесей вернулся с Крита после победы над Минотавром, использовался афинянами для ежегодного паломничества на остров Делос. Перед каждым плаванием корабль чинили, заменяя часть прогнивших досок на новые. Спустя какое-то время все старые доски корабля были заменены на новые. Среди философов разгорелся спор: тот же этот корабль, на котором плавал Тесей, или уже другой - новый?

Согласно Платону, корабль - всё тот же, потому что стоящая за ним идея всё та же. Согласно наивному материализму, корабль уже другой, так как вся материя в нём сменилась на другую.

У этого парадокса есть продолжение:

А что, если бы старые доски сохранили и сколотили бы из них второй корабль? Какой из этих двух кораблей был бы настоящим и почему?

А недавно один из зрителей моего выступления в рамках проекта Унивёрс предложил ещё один мысленный эксперимент - обратный парадокс корабля Тесея:

Если корабль не чинили, и все доски в нём остались теми же самыми, что и были, но теперь на нём не совершают паломничество на остров Делос, а используют в качестве магазина по продаже мороженного, тот же это корабль или нет?

По Платону, если идея корабля сменилась, то корабль мороженщика - это уже не оригинальный корабль Тесея.

Философ Джордж Бёркли рассуждает о том, что не все идеи воплощены в материальной реальности - идеи могут быть собраны из других идей. Например, взяв идею лошади из наблюдения за лошадьми и идею рога из наблюдения за рогатым скотом, человек объединил две эти идеи в идею единорога, которая не имеет материального воплощения, но, по идее, при успехах генной инженерии, иметь его может.

Давайте разберём утверждение о субстанциональности идей, которое в философии известно как реализм. Согласно реализму, идеи существуют сами по себе независимо от материи и служат прообразом материальных вещей, предстоят им, или же наоборот абстрагируются из вещей наблюдением за ними. Например, идея круга существует независимо от всех круглых вещей, но воплощается в них и может быть извлечена из наблюдения за множеством круглых предметов. По сути, согласно реализму, материальные предметы - это просто материя, принявшая форму определённой идеи. Если это так, то между идеей и материей как между двумя независимыми субстанциями должна быть некая связь - что-то, что их связывает вместе. Реальна ли в онтологическом смысле сама эта связь?

Если реальна, то есть сама по себе является субстанцией, то значит нужна связь второго порядка между самой идеей, связью между идеей и её материальным воплощением и самим этим материальным воплощением. Тут мы уходим в бесконечный регресс. Если же эта связь нереальна, то тогда идея никак не связана с материальной вещью, в которой она воплощена. Может быть идея и материя - это одна и та же субстанция?

Но если идея тождественна своему материальному воплощению, то значит универсальных идей не может существовать - если каждая кошка воплощает абстрактную идею кошкости, то этих кошкостей существует столько же, сколько и кошек и они вообще не связаны между собой. Если же одна и та же универсальная идея тождественна сразу множеству материальных воплощений, то получается, что идея пространственна, что противоречит внепространственности идей по определению Платона - два плюс два в любой точке мира равно четырём. Может быть, в каждой кошке есть доля идеи кошкости? Но тогда получается, что идея делима и при изменении одной из кошек изменяется сама, а, согласно Платону, идеи вечны и неизменны во времени - в любой момент истории два плюс два равно четырём. Может быть, идеи просто не существуют вообще? Но как тогда объяснить, что два плюс два всегда и везде получается равным четырём?

Получается, что любые воззрения на природу платоновских идей как независимых сущностей логически несостоятельны. Мы не утверждаем, что идей не существуют вообще - конечно, они существуют. Но идеи не обладают собственной независимой природой, не существуют как независимая субстанция. Идеи - это просто обозначения отдельных узлов в сети взаимоотношений. Эту идею хорошо описывает буддийская Гандавьюха сутра:

Мир подобен сети Индры из драгоценных камней, охватывающая собой весь мир. При этом каждый из каменьев отражал все остальные камни и сам также отражался в них: все в одном, одно во всем, все во всем, одно в одном.

Мы стоим посреди этого лабиринта отражений и смотрим вокруг себя. Видим ли мы отражения? Конечно, видим. Есть ли то, что отражается? Нет. Но, может, идей как субстанции не существует, но существует независимо только материя?

Материя

Немецкий физик Макс Планк писал:

Как человек, посвятивший всю свою жизнь самой ясной науке и изучению материи, в результате своих исследований об атомах я могу сказать вам следующее: материи как таковой не существует. Всякая материя возникает и существует только благодаря силе, которая приводит частицу атома в вибрацию и удерживает вместе эту мельчайшую солнечную систему атома. Мы должны предположить, что за этой силой существует сознательный Разум. Этот Разум - матрица всей материи.

Почему Планк считал, что материи не существует, а она - лишь продукт ума?

Давайте разберёмся на простом примере. Представления о субстанциональности материи опираются на мереологический нигилизм -  философскую позицию, согласно которой объекты, состоящие из частей, не существуют, а существуют лишь базовые кирпичики, из которых эти объекты собираются. Наши человеческие тела состоят из биологических клеток, клетки состоят из молекул, молекулы из атомов, атомы из элементарных частиц. Согласно мереологическому нигилизму, тела, клетки, молекулы и атомы не существуют - это просто абстракции над совокупностью процессов взаимодействия элементарных частиц. Но можем ли мы сказать, что элементарные частицы и правда обладают независимым существованием?

Нет. Дело в том, что чем глубже мы спускаемся вниз по иерархии уровней материи, тем всё более и более абстрактными становятся объекты каждого следующего уровня. Элементарные частицы, согласно квантовой механике - это не шарики из учебников физики для седьмого класса, а волны амплитуды вероятности, которые при взаимодействии друг с другом на мгновение проявляют себя как частица. Вне этого краткого мгновения у них нет ни точного положения в пространстве, ни точного импульса, их движение подчиняется волновому уравнению Шрёдингера, в котором присутствует такой губительный для наших представлений о "твёрдой" материальности член как мнимая единица, равная корню из минус одного.

По сути, элементарные частицы представляют собой математические абстракции, описывающие какие-то узлы взаимоотношений между объектами в нашем мире, о которых мы можем только сказать, в каких именно взаимоотношениях они участвуют и с какими численными коэффициентами. Можно ли тогда сказать, что никакой материи не существует вовсе? Конечно же нет. Просто материя - это не субстанция, а имя для некоторых узлов в сети взаимоотношений. Одно из отражений в лабиринте зеркал.

Сознание и квалиа

Сознание - это одна из величайших загадок Вселенной. Почему мы чувствуем и ощущаем? Почему у происходящего в мире есть эта неописуемая субъективная сторона опыта? Почему мы видим это недоступное никому другому "внутреннее кино"?

Сознание представляет собой поток элементов субъективного опыта - квалиа. Нагарджуна и другие индийские философы того времени вместо "квалиа" обычно используют схожий буддийский термин "дхарма". Квалиа - это элементарная частица субъективного опыта. Красный цвет, звук хлопка, запах розы, вкус шоколада, тактильное ощущение шероховатости деревянной поверхности, чувство радости, ощущение боли - это всё квалиа.

Квалиа не сводимы к физике. Физика описывает количественный аспект мира - отношения объектов друг с другом, квалиа же описывает качественный аспект мира - как оно ощущается. Само слово "квалиа" переводится с латыни как "качества". Учёный может всю жизнь изучать летучих мышей, может ответить на любой физический вопрос об устройстве их эхолокации, но никогда не сможет познать, каково это быть летучей мышью, каково ощущать эхолокацию. Это самое "каково" и есть сознание.

Как объяснить слепому от рождения человеку, что такое красный цвет? Красный цвет не сведёшь к физике. Мы можем видеть цвета во сне, а значит цвета нет ни в свете определённой длины волны, ни в строении глаза. Да и найти цвет в активации нейронных цепочек в определённых областях головного мозга нельзя. Да, все эти вещи связаны и как-то коррелируют с нашим впечатлением - если выколоть себя глаза, то красных яблок нигде кроме как в воображении больше не увидишь, но красный цвет несводим ни к физическому описанию света, ни к биологическому строению глаза, ни к строению мозга. Качественное не сводится к количественному.

При этом утверждение о существовании сознания - это метафизическое утверждение. Мы не можем никаким научным методом доказать даже самому себе, что у другого человека или животного есть сознание, хотя факт наличия сознания у нас самих для нас самоочевиден. Мы не можем посмотреть на мир глазами другого человека. Эту проблему знаменитый немецкий математик и философ Готфрид Лейбниц окрестил «проблемой других умов». И даже если мы начнём пытаться объяснить своё собственное сознание, то в определённый момент наткнёмся на разрыв в объяснении между физическим и квалиа. Таким образом, утверждения "сознание существует" и "сознание не существует" - метафизические, недоказуемые и неопровержимые.

С вопросом существования сознания тесно связан вопрос существования внешнего по отношению к сознанию мира. Немецкий философ Иммануил Кант писал, что всё, что мы знаем о мире, мы получаем через феноменальный опыт, то есть с помощью квалиа, а то, какие вещи ноуменально, какие они сами по себе, нам знать не дано. Вода определённого цвета, определённого вкуса и мокрая только в сознании, а что за ноуменальный объект стоит за этим феноменальным опытом мы не знаем. Мы можем построить физическую модель воды, которая будет давать точные предсказания, но эта модель - не есть реальность. Карта - это не изображённая на ней территория.

Может быть никакого внешнего мира нет, и всё, как считают солипсисты, происходит лишь в нашем единственном сознании. Или, может быть, злые учёные засунули наш мозг в банку и подключили к нему электропровода, и вся реальность, что мы видим вокруг - это лишь компьютерная симуляция. Существование внешнего объективного мира за пределами сознания - это тоже метафизическое утверждение, никак не доказуемое и никак не опровергаемое.

Одной из основных проблем в философии сознания считается проблема духа и тела - вопрос о взаимоотношении сознания и материи. Если сознание несводимо к физическому описанию, то есть к тому, что можно считать материей, то появляется вопрос его взаимодействии с материей. На этот вопрос есть несколько философских ответов.

Дуализм утверждает, что и сознание, и материя субстанциональны и влияют друг на друга. Слабой точкой этой позиции служит вопрос о том, как именно одно влияет на другое. Как может желание в сознании привести к движению материальной руки? Как удар по материальной руке может привести к боли в сознании. Между сознанием и материей, если они субстанциональны, должна была бы быть какая-то связь, но если эта связь есть, то она должна быть тоже субстанциональна и быть связана и с тем и с другим. Тут, как и в случае с идеями и материей, мы приходим к бесконечному регрессу. Если же эта связь не субстанциональна, то тогда сознание и материя никак не связаны друг с другом, а следовательно не могут друг на друга влиять.

Кроме того, против дуализма говорит причинная замкнутость нашего тела и мозга - мы можем проследить всю цепочку причин и следствий для каждого процесса в нашем теле - активация нерва на коже, идущий по нервам в головной мозг сигнал, активация нейронов, прохождение цепочки принимающих решение нейронов в мозгу, активация идущего по нервам электрического сигнала к руке, сокращение мышц руки, поднятие руки. Никакого сознания в этом процессе нет. Все причины происходящего в материальном мире находятся внутри этого материального мира.

Эпифеноменализм чем-то похож на дуализм - он тоже утверждает, что и сознание, и материя субстанциональны. Его отличает от дуализма то, что, согласно эпифеноменализму, только материя влияет на сознание, а сознание просто отражает материальные процессы. Внутренне кино проигрывается только для субъективного наблюдателя, но это кино никак не влияет на материальную реальность. Но тогда непонятно как мы вообще можем произнести слова о сознании своим материальным ртом, если сознание не влияет на материю - ведь рот говорит только то, что ему скажет мозг, а мозг, как мы уже сказали, причинно замкнут внутри материального мира - причинно-следственный импульс для произношения слов "у меня есть чувство красного" приходит из материального мира.

Физикализм утверждает, что существует только физическое, а сознание сводимо к физическому. Это одна из самых слабых позиций, так как показать, как именно сознание может быть сведено к физическому, физикалисты не могут. Более того, всё, что мы знаем о физике, мы узнали через квалиа - то есть квалиа в некотором смысле первичны, а наши представления о физическом вторичны. Есть более интересная версия физикализма - иллюзионизм, который утверждает, что есть только физическое, а на самом деле сознания нет, а нам только кажется, что оно есть - эта иллюзия, по их мнению, создаётся рефлексией, когда процессы в мозге пытаются получить доступ к своим собственным частям. Против иллюзионизма не нужна даже особая критика - опровержение в виде существования цветов стоит у нас прямо перед глазами. Как может быть иллюзией то, что я вижу красный цвет? Само видение красного уже есть факт - что в данном случае вообще может значить слово иллюзия?

Панпсихизм полностью противоположен физикализму - он утверждает, что существует только сознание, а вся материя - это отношения одних квалиа к другим. Ведь если физика описывает количественные отношения, но не говорит, что именно относится к чему, то это фундаментальное что-то, что вступает в отношения должно быть не количественным, а качественным. А единственное качественное, что мы знаем - это квалиа. Панпсихизм - самая логичная из философиских позиций о природе сознания, но и у него есть свои проблемы. Если квалиа присущи всему сущему, начиная от элементарных частиц, то значит сложный сознательный опыт человека состоит из более простых переживаний. Но тогда встаёт проблема комбинации - почему я чувствую себя целиком, а моя коленка не чувствует себя целым? Или коленка тоже чувствует? Как тогда складывается этот опыт и почему в организме есть куча бессознательно происходящих процессов - например, дыхание, пищеварение, и так далее?

Более интересная форма панпсихизма - космопсихизм - утверждает, что есть единое вселенское сознание, и оно не собирается из элементарных кусочков, а наоборот раскалывается на эти кусочки. То есть если панпсихизм идёт снизу вверх, то космопсихизм сверху вниз - от единого сознания к конкретным сознаниям. Я писал о космопсихизме в эссе "Метафизика, космопсихизм и перводвигатель: есть ли сознание у камней?". У этой философии тоже есть свои проблемы: если сознание едино, то как возможна множественность опыта? Почему вы не чувствуете мою боль? Почему переживания не сливаются вместе? Если есть какие-то локальные границы, отделяющие одни сознания от других, то это сознание уже не едино.

Все философские позиции о природе сознания имеют свои интересные моменты, но все они, если мы считаем сознание чем-то субстанциональным, в конце концов приходят к абсурду и самопротиворечию. Поэтому сознание не может быть независимой субстанцией. Это легко продемонстрировать даже на примере квалиа цвета - красный цвет не может существовать независимо сам по себе, потому что он, как минимум, требует наличия двухмерной поверхности, чтобы существовать - без окрашенной поверхности нельзя увидеть цвет.

Квалиа в буддийской философии не приписывают независимого существования - это просто постоянно возникающие и тут же исчезающие элементы потока субъективного опыта. Религиовед Иван Негреев сравнивает этот поток опыта с пикселями на экране - когда мы смотрим фильм мы верим в него, переживаем за главных героев, но весь фильм - это просто поток сменяющих цвета пикселей. Пиксели меняют цвет быстрее, чем на них можно обратить внимание. Существует ли фильм, идущий на экране? Да, конечно, мы же его смотрим. Но обладает ли этот фильм независимым существованием? Нет, он иллюзорен в том смысле, что образован сменой цвета пикселей. То же самое и с реальностью вокруг нас, только в отличие от пикселей на экране дхармы-квалиа ещё быстрее - они не существуют даже мгновения. Когда мы обращаем на них внимание, они уже в прошлом. Существует ли окружающий наш мир? Да, существует. Обладает ли он независимым существованием? Нет.

Можно ли сказать, что внешний по отношению к нашему сознанию объективный мир существует? Нельзя этого отрицать, но невозможно этого и с уверенностью утверждать. Если внешнего мира ноуменальных вещей нет, то откуда тогда поступают нам их феноменальные проявления - формы, цвета, запахи? Если он есть, то какая связь между ноуменами и феноменами? Если эта связь реальна, то мы как всегда скатываемся в бесконечный регресс. А если эта связь нереальна, то ноумены, кантовские вещи в себе, никак не связаны с феноменами, но тогда откуда мы можем знать об их существовании?

В любом случае, если мы привязываемся умом к возможности независимого существования сознания или материи, ноуменов и феноменов, объективного и субъективного миров, то мы приходим к самопротиворечивым философским теориям. Единственный вариант - отвязать ум от всех теорий и принять, что все эти оппозиции - суть разные аспекты одного и того же графа реальности. Субъект и объект возникают взаимозависимо, ноумены и феномены возникают взаимозависимо, сознание и материя возникают взаимозависимо. Нет сознания без материи и материи без сознания. Нет объектов без субъекта и субъекта без объектов. Нет феноменов без ноуменов и нет ноуменов без феноменов. Эта неразделимые аспекты одного и того же мира.

Пространство

Несмотря на появление в начале XX века теории относительности Эйнштейна, в массовом сознании людей пространство до сих пор представляется по-ньютоновски - этакой сценой, внутри которой существуют физические объекты. Теория относительности опровергает подобную картину - согласно Эйнштейну, разделение реальности на пространство и время зависит от наблюдателя.

Представьте себе наблюдателя в абсолютно пустом мире, в котором нет ничего кроме этого самого субъекта-наблюдателя. Сможет ли этот наблюдатель утверждать существование в таком мире пространства? Нет. А теперь представьте себе наблюдателя в мире, где существует всего один точечный объект. В таком мире наблюдатель сможет сказать, что пространство существует, но он не сможет измерить никаких расстояний, так как кроме одного объекта, который мы можем взять за точку отсчёта, у него ничего нет. А теперь представьте себе наблюдателя в мире, где существуют два точечных несовпадающих друг с другом объекта. В таком мире наблюдатель сможет утверждать существование одномерного пространства, так как можно провести через две точки прямую и, взяв одну из них за точку отсчёта, задать точку второго объекта на этой линии за единицу.

Связь между пространством и объектами в нём здесь точно такая же как между идеями и материей - пространство определяется находящимися в нём объектами, а сами эти объекты могут быть восприняты лишь внутри пространства. Одно без другого существовать не может. Если мы попытаемся утвердить независимое существование пространства, то придём в тупик - у пустого пространства без объектов нет никаких свойств, даже измерений, а утверждать независимое существование чего-то у чего нет свойств - бессмыслица. Таким образом, пространство - это тоже не субстанция.

Продолжение во второй части.

За свою жизнь я перепробовал кучу различных методов и техник для продуктивного ведения своих дел - различные таск-трекеры, GTD и Pomodoro. Эти методы были отнюдь не бесполезны и до сих пор приносят мне хорошие результаты, но истинного пика продуктивности я достиг лишь открыв для себя несколько простых принципов из китайской философии даосизма.

Три ресурса

У любого человека есть три основных ресурса:

• Время

• Деньги

• Запас сил

Под запасом сил здесь я имею в виду внутреннюю психологическую энергию человека, его способность превращать предоставленные судьбой потенциальные возможности в актуальное действие, внутренний психологический заряд воли к действию. Про важность запаса психологических сил часто забывают, а это чуть ли не важнейший из ресурсов - без него наступает паралич воли, и продуктивность падает в ноль.

Все три этих ресурса легко можно конвертировать друг в друга, так как все они - по сути, разные формы энергии. Как вы помните из школьного курса физики, энергия может существовать в разных формах: кинетической, потенциальной, тепловой, электромагнитной. Даже масса, как мы знаем из знаменитого уравнения - это тоже просто концентрированная энергия. Время в физике тоже связано с энергией: согласно знаменитым теоремам Нетёр, закон сохранения энергии - это прямое следствие симметрии и однородности физических систем во времени.

Если проводить аналогии с физикой, можно сказать, что деньги - это, как и масса, концентрированная энергия. Проверить это утверждение легко - вы можете заказать уборку в квартире, оплатить её деньгами, тем самым высвободив заложенную в них энергию, которая пойдёт на уменьшение энтропии, то есть беспорядка, в вашем доме.

Дао продуктивности

Древние китайские даосы представляли мир как неописуемую словами энергию Дао, предстающую перед нами в кажущихся противоположными формах Инь и Ян, постоянно перетекающих друг в друга.

Если мы поразмышляем о том, что такое энергия в физике, мы обнаружим, что это нечто, принимающее различные формы, которые постоянно перетекают друг в друга: кинетическая в потенциальную, потенциальная в кинетическую, электромагнитная в тепловую, и так далее. Но можем ли мы словами описать, что такое энергия? Вряд ли. Мы видим её во всём сущем, но чётко сформулировать, что же она такое, не можем.

Даосы утверждали, что главное в жизни - найти гармонию, баланс между всеми формами Дао, настроить ритмы перетакания различных воплощений Дао друг в друга. То же самое верно и для ресурсов человека - главное, найти баланс между тремя формами энергии. Только при гармоничном распределении всех трёх ресурсов человек выходит на пик своей продуктивности.

Если у человека есть время и деньги, но нет запаса сил и воли к жизни, то он будет жить в постоянной депрессии, прожигать жизнь, убивать время думскроллингом соцсетей, заниматься бессмысленным потреблением. Если у человека есть время и запас психологической энергии, но нет денег, то он будет сильно ограничен в возможности воплощения в жизнь своих идей и проектов, ведь в большинстве случаев за деньги можно срезать путь, пройти более короткой дорогой, сильно сэкономив время и силы. Если у человека есть деньги и энергия действовать, но нет времени, так как он постоянно в работе, то у него просто не будет возможности воплотить в жизнь всё им задуманное.

Ресурсы можно конвертировать друг в друга. Потратив время и деньги на хороший отпуск можно восстановить запас сил. Потратив время и силы можно заработать денег. Потратив деньги на найм другого человека и делегировав тому какую-то деятельность, можно купить себе свободное время и силы - например, в уже приведённом мною примере с наймом уборщицы вы экономите время и силы, которое потратили бы на уборку сами.

Для гармоничной жизни эти ресурсы, как завещали даосы, должны находиться в постоянном круговороте, перетекая друг в друга, и быть сбалансированными. Иногда следует пожертвовать временем и силами, чтобы заработать денег, иногда наоборот лучше потратить деньги, чем заниматься чем-то самому. Никогда нельзя нарушать баланс и копить один ресурс в ущерб остальным двум. Если мы концентрируемся на накоплении денег, тратя всё своё время и силы, или наооборот тратим всё своё время и деньги на удовольствия и развлечения, то мы тем самым постоянно воруем из кассы одного ресурса, чтобы вложиться в кассу другого. Делая это слишком часто, мы очень быстро придём к ресурсному кассовому разрыву и полному разрушению нашей жизни. Например, постоянная нехватка свободного времени и отсутствие сил приведут к тому, что все накопленные деньги не принесут никакого удовольствия и удовлетворения - в итоге мы забьём и на зарабатывание денег, и скатимся в депрессивное положение без денег и без воли к жизни. Для постоянного баланса ресурсов нужно заниматься не только управлением своими финансами и тайм-менеджментом с помощью систем вроде GTD, но и управлением своей энергией. Только гармонично распределяя эти ресурсы и конвертируя их из того, которого переизбыток, в тот, которого недостаток, мы сможем выйти на пик своей продуктивности.

КПД наших действий

Из школьного курса физики мы помним, что у любого двигателя есть КПД - коэффициент полезного действия, говорящий о том, какой процент из всей потраченной энергии пошёл на выполнение действительно полезной работы. Если мы рассмотрим человека как двигатель, меняющий мир вокруг себя, то у него мы тоже можем найти коэффициент полезного действия. Как его вычислить?

Итальянский инженер Вильфредо Парето как-то заметил, что в среднем в любом деле 80% результата достигается с помощью 20% усилий, а остальные 80% усилий уходят на достижение последних 20% результата. Это наблюдение стало известно как правило Парето. В некоторых делах нам и не нужно быть перфекционистами и достигать стопроцентного результата - достаточно только найти те самые нужные 20% усилий, которые дадут нам 80% нужного нам результата. Правило Парето известно довольно широко, но вот что мало известно - так это строгий математический вывод из рекурсивного применения правила Парето к самому себе.

При применении правила Парето к нему самому мы обнаруживаем удивительное: если 20% из всех усилий дают 80% результата, то значит 20% от 20% усилий дадут 80% от 80% результата, то есть 4% усилий дадут 64% результата. А на следующей итерации уже только 0.8% усилий приведут к достижению 51.2% результата - то есть, грубо говоря, применив всего процент правильно направленных усилий мы можем получить половину результата. Это говорит о том, что действовать с умом гораздо важнее, чем быть усердным.

Кроме того, есть ещё одно наблюдение, уже моё собственное. Чем быстрее мы движемся в выполнении своих дел, тем больше нам противостоит вязкость окружающей среды. Ничего не делая, мы не ощущаем сопротивления среды, но как только мы начинаем что-то делать, каждое наше действие приводит к столкновению с разными проблемами, преодолевая которые мы наталкиваемся уже на новые проблемы. И чем быстрее мы движемся, тем на большее количество проблем в день мы наталкиваемся. Из этого можно сделать два вывода. Первый состоит в том, что в пословице "тихо едешь - дальше будешь" есть много мудрости. Второе - в том, что чтобы двигаться у успеху не тихо, а максимально быстро, нужно научиться перестать быть перфекционистом, без жалости резать хвосты неприоритетных проектов и научиться фиксировать убытки в нужный момент.

Надеюсь, что мои наблюдения о ресурсной модели человеческой продуктивности и о КПД человеческих действий, помогут вам в ваших собственных делах. У меня есть телеграм‑канал, в котором я пишу о философии, математике, буддизме, кибернетике, продуктивности. Туда я часто выкладываю то, что из‑за тематических ограничений не могу публиковать на Хабре.

Также можете прочитать два моих прошлых поста на тему продуктивности:

• Как я победил прокрастинацию, узнал свои истинные желания, поставил четкие цели и достиг их

• Панель управления собой: 10 простых шагов к порядку в вашей жизни