ビレブン / B11

@b11mech

Добрый день, уважаемые Пикабушники!

Сегодня, во время прогулки по городу, пришла мне в голову одна очень, как по мне, интересная мысль. Но, рассуждая о ней, пришёл к некоторому противоречию и надеюсь, что вы сможете с этим разобраться.

Предупреждаю сразу! Всё что будет ниже - связано с математикой.

Ну, поехали!

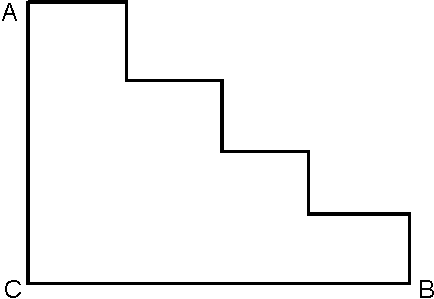
Давайте рассмотрим фигуру, состоящую из прямого угла и ломанной, соединяющей концы сторон, данный угол образующих.

Пусть длина стороны АС в данной фигуре равна а, а длина стороны ВС = b. Вопрос, чему равна длина ломанной АВ?

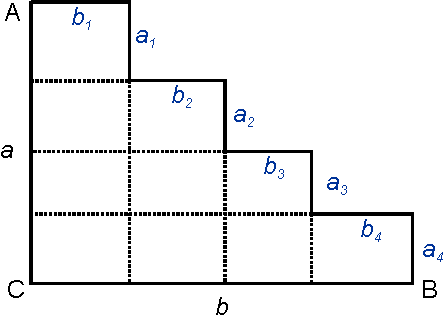
Самый простой вариант в данном случае – разбить ломанную на отдельные «кусочки», параллельные либо стороне ВС, либо стороне АС. Длину каждого «кусочка» обозначим через ai, если данный «кусочек» параллелен стороне АС, и bj – если параллелен ВС.

Тогда, длина ломанной АВ будет складываться из сумм всех ai и bj. Но, из рисунка понятно, что сумма всех ai равна а, то же справедливо для bj и b. Соответственно, длина ломанной АВ будет равна a+b.

А теперь, давайте представим, что у нас не 4 «ступеньки» в ломанной АВ, а, например, 10. Как вы понимаете, по сути, изменятся уменьшатся только значения ai и bj. Длина ломанной АВ как была a+b, так и осталась.

И вот тут самое интересное (надеюсь)! А что, если увеличивать число «ступенек» до 1000? До миллиона? До миллиарда? До бесконечности?

Тогда, наши ai и bj будут стремиться к 0, но сумма всех этих отрезков – также останется a+b.

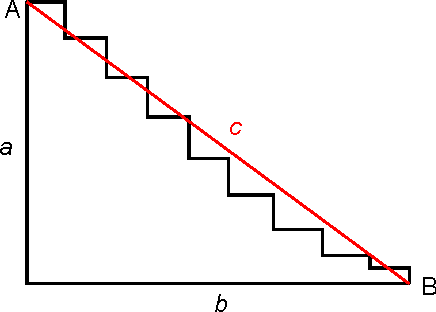
И вот тут как раз возникает проблема, о которой я писал ранее: если мы будем увеличивать число «ступенек» бесконечно, то, по сути, будем иметь не ломанную, а отрезок АВ, который, о чудо, является в данной фигуре еще и гипотенузой. Ну, а как мы все знаем из курса школьной геометрии, квадрат гипотенузы равен сумме квадратов катетов, т.е. с^2=а^2+b^2

Вот и получается, что если на АВ смотреть как на ломанную, пусть даже ломанную бесконечно, то её длина должна быть a+b, а если смотреть как на гипотенузу – √ (а^2+b^2)

Собственно вопрос: где мои рассуждения неверны? Почему такой парадокс происходит?

Прошу сильно не пинать!

Работаю учителем математики в школе. Загорелся идеей сделать серию наглядных пособий по геометрии про равенство площадей на основе экспоната в музее занимательных наук "Эксперементаниум", типа вот такого

Есть кроме теоремы Пифагора много теорем, основанных на методе перекладывания площадей. Хочу начать с теоремы попроще: о том, что медиана делит треугольник на два треугольника, равных по площади.
Теперь к сути поста: я не силен в плане... Эм, любом, кроме математики. Хотел взять 3 листа из материала, типа оргстекла (пластик), сделать три круга одинакового размера (или купить прямо круги): два оставить как есть, в третьем, (для теоремы Пифагора) вырезать три квадрата, как на картинке выше, и поместить круг с вырезами между двумя целыми кругами.
Вопросы к знающим людям: что лучше подойдет как материал типа оргстекла - достаточно прочное, но легкое в обработке, поскольку, естественно, специального инструмента не имею. Желательно чтобы хорошим резаком можно было вырезать в нём нужные фигуры, шкурочкой или другим каким образивом зачистить.
Второе: эти листы надо будет склеить клеем-герметиком, который к тому же станет полностью прозрачным после высыхания. Есть такой клей?
Ну и последнее - с водой много заморочек, хотя, с точки зрения "перетекания" Между квадратами, она подходит идеально. Но хотел попробовать более простые вещи: мелкие шарики либо песок. Что кроме воды может подойти?
P. S. В интернете нашел одну ущербную модель типа как на фото, но не устроила по качеству, и, напомню, у меня идея сделать не только эту теорему, а целый ряд теорем таким же способом, а вот этого уже нигде нет.

Приветствую Вас, уважаемые Читатели! Сегодня хочу Вам рассказать одну занимательную историю из юридической практики, когда от теоремы Пифагора буквально зависел достаточно большой срок заключения. Перенесемся же в Нью-Йорк начала 21 века. Поехали!

В марте 2005 года в Нью-Йорке на пересечении 40-й Западной улицы и 8-й авеню в Манхэттене некто Джеймс Роббинс был задержан за сбыт не самых законных веществ.

Всё бы ничего, но оказалось, что тяжесть преступления усиливается, ведь торговля проводилась менее, чем в 1000 футах от ближайшей школы - Holy Cross School, находившейся на 43-ей западной улице.

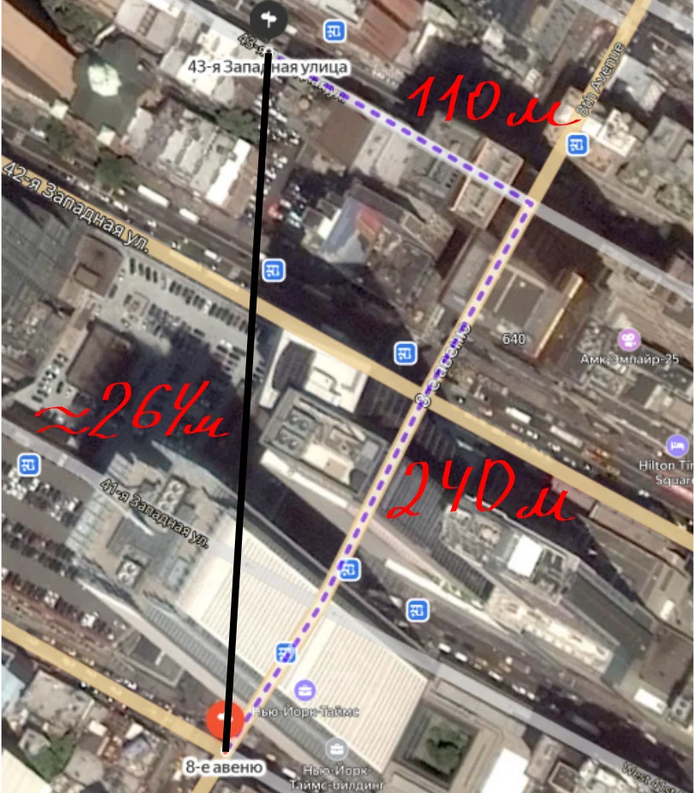
Впрочем, это была позиция обвинения, адвокаты подозреваемого были совсем другого мнения. Взгляните на карту:

Адвокаты рассуждали так: чтобы непосредственно дойти от места задержания до входа в школу необходимо пройти по 8-й авеню, а затем свернуть на 43-ю западную - итого по карте примерно 350 метров, что в переводе в буржуйские единицы равняется примерно 1160 футов.

Прокурор же вместе с полицейским департаментом настаивал, что для измерения расстояния необходимо применить теорему Пифагора: в этом случае расстояние по прямой будет равняться чуть менее 900 футов, которые выльются в 5-6 дополнительных лет тюрьмы в связи с отягчающими обстоятельствами.

Интересно, что у американцев выражение "расстояние по прямой" звучит как "as the crow flies" - дословно, "как летит ворона".

Все доводы адвокатов, что расстояние надо измерять по реально возможному маршруту, а "вороны, дескать, наркотики не продают", не были услышаны судом присяжных из 7 человек, и Джеймс Роббинс получил более тяжкую статью.

(PROOF) - судебное решение, дело " Граждане против Джеймса Роббинса"

Это далеко не единственный случай подобного рода споров, но, в целом , американскую судебную практику можно назвать "пифагорейской", потому что такие вопросы всегда трактуются в пользу измерения расстояния по прямой. Спасибо за внимание!

Больше интересной математики в телеграмм - "Математика не для всех"