Найдено тут.

Ссылка на прошлый пост: http://pikabu.ru/story/mnozhestvo_mandelbrota_5071307

Ссылка на позапрошлый пост: http://pikabu.ru/story/fraktal_zhulia_5056476

В прошлый раз я тут выложил несколько гифок, красочно описывающих фрактал Мандельброта, и мне пришло в голову его немного модифицировать.

Как все мы знаем, множество Мандельброта обычно выглядит так

Как получается такая вещь? Для начала, небольшое отступление.

Данная плоскость, показанная на картинке - не та, которую обычно изучают в школе, а комплексная. Что это значит? То, что каждой точке на ней соответствует число (x + yi), где i - корень из -1. Да, из отрицательных чисел обычно нельзя извлечь корень, но математики те еще шутники, поэтому выдумали специальное обозначение для таких вот вещей.

Благодаря тому, что каждая точка на комплексной плоскости является еще и числом, с ней можно производить те обычные математические действия, какие невозможно совершать на обычной плоскости, как, например, умножение, возведение в квадрат, и так далее.

Так вот, для получения множества Мандельброта берем случайную точку В с координатами (х, у), и точку А с координатами (0, 0). Затем мы умножаем точку А саму на себя (получится опять же нулевая точка), а потом прибавляем к ней точку В.

Если полученная точка выходит за круг радиуса 2, тогда все шикарно. Если нет, то снова проделываем те же манипуляции: умножаем получившуюся точку саму на себя, прибавляем точку В, и снова проверяем. Чем больше проходов требуется, чтобы достичь границы заветного круга, тем ярче становится точка. Если точка вылетает из круга после одной итерации - она почти черная. Если и за тысячу проделанных действий не удалось улепетнуть - она синяя (ну или любого другого цвета, в зависимости от выбранной палитры, моего настроения и моей великолепной силы духа). Иногда точка вообще не может выбраться из круга - вот именно тогда она и принадлежит множеству Мандельброта.

Ладно, надеюсь, вы поняли. Если не поняли, то вот ссылка, которая точно все разъяснит:

http://sunandstuff.com/mandelbrot/about/

-----------------------------------------------------------------------------------------------

Немного математики, или как я получил уравнение для вывода этого чертового фрактала

В ролях: точка А в роли точки А, точка В в роли точки В, и мисс Мурпл в роли мисс Бурпл.

А если серьезно, то можете пропускать эту часть, если вам не интересна математика, и хочется посмотреть на интересные картинки. Для остальных же: пусть точка А имеет координаты (a, b), а точка В - (x, y). Тогда А будет равно a+bi, В равно x+yi.

А * А + В = (a+bi)*(a+bi) + (x+yi) = (a*a + 2*a*b*i + b*b*i^2) + x + yi =

(a*a + b*b*i^2 + x) + (2*a*b + y) * i =

(a*a - b*b + x) + (2*a*b + y) * i

Так как точка А имела координаты (a, b), и именно ее нам и надо преобразовать, получим:

a -> a*a - b*b + x

b -> 2*a*b + y

-----------------------------------------------------------------------------------------------

Извращения (осторожно! много тяжелых гифок!)

Для начала я решил немного поиграться с уравнениями. Недолго думая, я решил взять второе уравнение по модулю. И получил неожиданный результат.

a -> a*a - b*b + x

b -> abs(2*a*b + y)

Ничем не отличается от обычного Мандельброта, такие же красивые неповторяющиеся узоры. Кто как, а я вижу тут зайца и лебедя. Одновременно.

Затем я взял по модулю первое уравнение. И лучше бы я этого не делал.

a -> abs(a*a - b*b + x)

b -> 2*a*b + y

Нет, это не член. Кого я обманываю. Клубничку ставить?

Отчаявшись, я взял по модулю оба уравнения.

a -> abs(a*a - b*b + x)

b -> abs(2*a*b + y)

К своему удивлению, я получил офигенскую картинку с бесконечным количеством одних и тех же повторяющихся узоров.

Интересные наблюдения: если поставить модуль напротив x или y, то картинка просто станет симметричной относительно горизонтали или вертикали. Также бесполезно ставить минус напротив них, картинка после этого просто станет зеркальной.

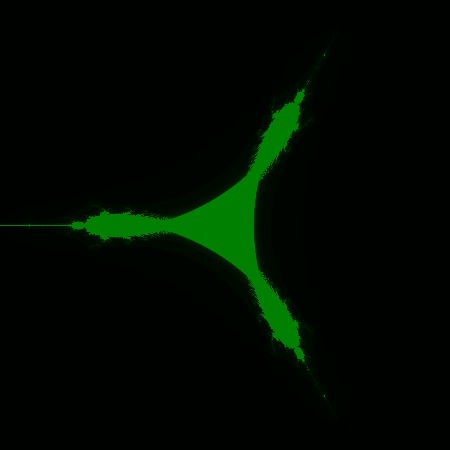
Когда действия с модулями кончились, просто умножил второе уравнение на -1.a -> a*a - b*b + xb -> -2*a*b - y

Получил красивую трехпалую фигню, похожую на космический корабль снизу. Нет, это удивительно, я просто поменял знак уравнения, а какой эффект, это же просто ААаааааааа... Кхм. Я отвлекся.

Если поменять знаки только у первого уравнения, получится то же самое. Если поменять у обоих, получится... ни за что не догадаетесь. Множество Мандельброта.

Приступаем к самому вкусному. Тригонометрия. Синус, если точнее.

a -> sin(a*a - b*b + x)

b -> 2*a*b + y

Получилась интересная красивая модификация Мандельброта, из которой вырываются всполохи зеленого нечто, похожие на протуберанцы у Солнца.

То же самое, но косинус появляется у второго уравнения.

a -> a*a - b*b + x

b -> cos(2*a*b + y)

Как будто множество Мандельброта вывернули наизнанку. Или паутина с кучей дыр.

Прибавляем синус к первому уравнению, и модуль ко второму.

a -> sin(a*a - b*b + x)

b -> abs(2*a*b + y)

И снова вывернутый наизнанку Мандельброт. На этот раз узор отличается цветочностью и клиньями. Ну, все синусы чем-то таким грешат.

На этот раз я решил возвести изначальное уравнение в куб (то есть получится А * А * А + В).

a -> a*a*a - 3*a*b*b + x

b -> 3*a*a*b - b*b*b + y

Почти ничем не отличается от Мандельброта, кроме изначального узора на первом кадре

Пойдем дальше, зачем нам какие-то простые кубы? Давайте четвертую степень!

a -> a*a*a*a - 6*a*a*b*b + b*b*b*b + x

b -> 4*a*a*a*b - 4*a*b*b*b + y

Аналогично. Такой же узор можно встретить и в Мандельброте

Как можно заметить, количество выпирающих пупырышек увеличивается с каждым увеличением степени. Для второй степени (т.е. Мандельброта) - одна пупырка, для третьей степени - две, для четвертой степени - уже три пупырки. Но допустим, степеней будет восемь.

Кстати, если взять у пятой степени первое уравнение по модулю, получится лягушка. На первой картинке снизу видна обычная пятая степень, на второй - лягуха.

Если изменить второе уравнение, а не первое - лягуха будет смотреть налево, а не вверх.

Кажется, все, а то и так слишком много. Оставшиеся гифки выложу потом, а то сайт не резиновый.

Полученные модификации математической ценности не имеют (наверное). Зачем же все это, спросите вы?