Что такое золотое сечение?
Все наверняка сталкивались с таким понятием как золотое сечение или золотая пропорция, или золотое число или даже божественная пропорция.
Это всё одно число, но называют его по-разному, а обозначают чаще всего греческой буквой φ. Оно равно 1,61803398874989… Но в чём такая популярность этого числа? В этой статье мы расскажем Вам о математике, истории и в проявление этого числа в математики, биологии и даже астрономии.
Математика числа φ
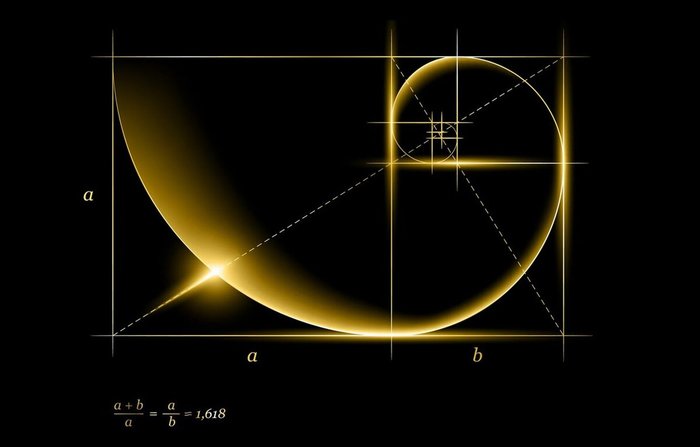
Число φ, как уже было заметно во введении, иррациональное и составляет (1+√5)/2. Согласно определению это число показывает, как отношение отрезка, разрезанного на две части разной длины, таким образом, что отношение всего отрезка к более длинной его разрезанной части равно отношению этой же более длинной части отрезка к более короткой.
С точки зрения математики, рассмотрим этот же отрезок и обозначим его более короткую часть как одну единицу, а длинную — х единиц. Тогда справедливо такое уравнение (x+1)/x=x/1. Запишем это уравнение как квадратное уравнение x2–x–1=0. Положительным корнем этого уравнения является x=(1+√5)/2 — это число и является золотым сечением.
Кроме этого, число φ имеет тесную связь с числами Фибоначчи. Если мы рассмотрим предел при (n→∞) отношении следующего члена последовательности Фибоначчи к предыдущему, то получим золотое число.
История числа φ
Историки считают, что понятие “золотое сечение” ввел Пифагор. При этом существует предположение, что он это понятие заимствовал у египтян или вавилонян. Действительно, пропорции пирамидов, храмов, украшений и даже предметов быта свидетельствуют, что египтяне часто пользовались этим соотношением.
Даже Леонардо да Винчи привлекал большое внимание изучению “золотого сечения”. Проводив многие исследования со стереометрическими фигурами, он заметил, что при определённых их сечениях образуются фигуры с отношениями сторон, которые равны числу φ.
В последующие столетия по принципам золотой пропорции создавались картины, произведения классической музыки, архитектурные сооружения, машины и даже мебель. Все были потрясены божественным числом и его красотой, поэтому они применяли его повсюду.
Другие проявления “золотого числа”
Золотое сечение показывает свое проявление даже в правильной пентаграмме, долгое время этот символ считался магическим во многих культурах. Здесь математика проста: точка пересечения её сторон делит эти стороны в золотой пропорции.
В биологии живые организмы обладают также определёнными свойствами, характерными для “золотой пропорции”. Некоторые пропорции тела, спиральные структуры и другие параметры. Учёные находили золотое сечение в структуре дерева, его ветвей и даже жилок на листьях. Кроме этого, такое же соотношение находят и в строении скелетов и разветвления вен, нервов у животных. Некоторые учёные даже выдвигали гипотезу о связи золотой пропорции с ДНК человека. При этом существуют мнения, что обнаружение золотого сечения в природе фиктивно.
Учёные проявления золотого сечения увидели даже в космосе. Оказалось, что соотношение периодов соседних планет равно числу φ. Кроме этого, некоторые параметры орбит планет тоже связаны с этим числом. Именно поэтому античные и средневековые учёные во всём искали порядок и закономерность, начиная с музыки и заканчивая движением небесных светил.
Картинка, от которой бомбит у всех дизайнеров1
Привет, это Роман из Логомашины. Когда я был дизайнером, частенько попадался такой клиент: «Все отлично, но вы же знаете — логотип должен быть построен по Золотому Сечению, тогда он подсознательно будет лучше восприниматься». И кидал эту картинку.
Тут у дизайнера дилемма: объяснять клиенту, что не так на этой картинке, или также криво приляпать «золотое сечение» к своему лого. Теперь вы можете просто отправить такому клиенту этот пост.
Что не так с этой картинкой
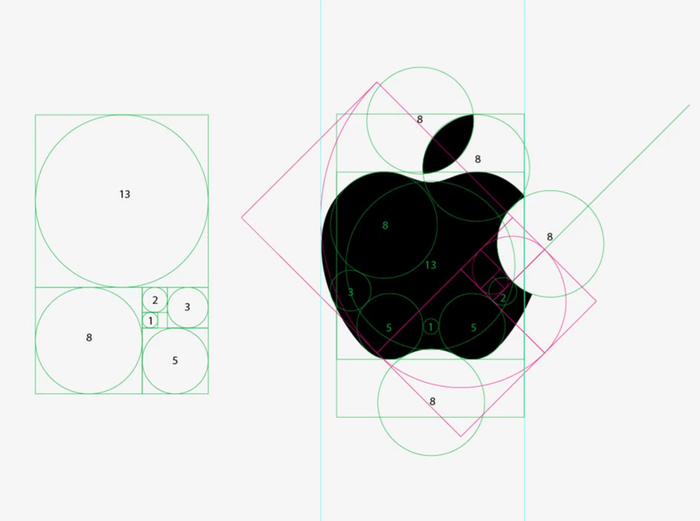
Если коротко — тут не так почти всё. Не нужно быть дизайнером, нужно просто внимательно посмотреть картинку и позадавать вопрос: «Почему этот кружок стоит именно так?». Станет понятно, что большинство кругов стоят как попало, а другие могли быть чуть больше или меньше — разницы нет.
Хочу поговорить про то самое «золотое сечение» (точнее, спираль Фибоначчи), на которое молятся некоторые заказчики — я обвел его жирным. Присмотритесь — ни одна его линия не совпадает с логотипом, как нарочно. Его просто налепили поверх как попало. Оно начинается в случайном месте, расположено под случайным углом, не повторяет форму ни одного контура, не строится ни по центру, ни по диаметру. Мне кажется, это просто стеб.
Тем не менее, многие клиенты присылают эту картинку, как образец утонченности форм и пропорций эпохи Возрождения. Не надо так.
Что не так с «Золотым сечением» в дизайне
Раз уж начал, расскажу, что не так с подходом: «В дизайне все должно быть построено по "Золотому сечению", это приятно глазу».
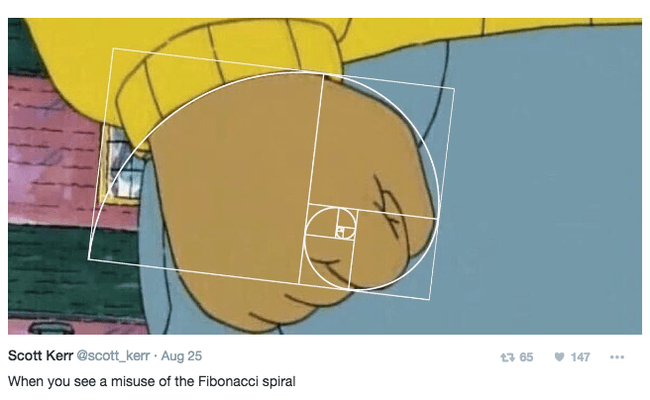
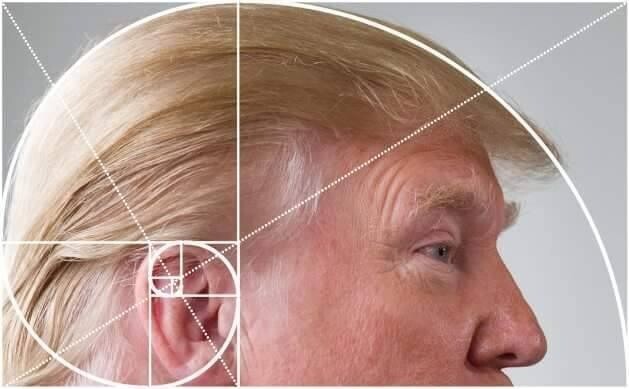
«Золотое сечение» можно разглядеть где угодно
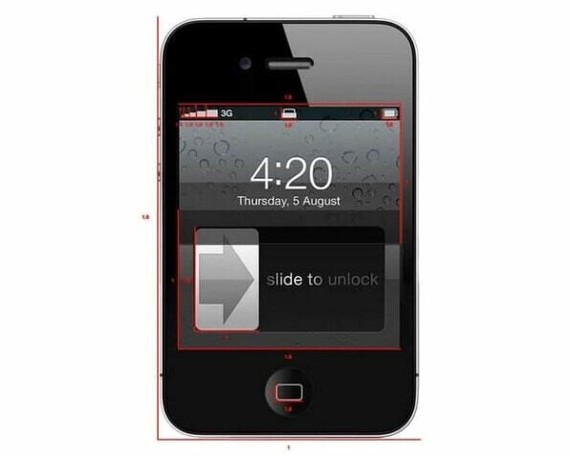
Ту самую «спираль» можно приляпать куда угодно — на красивое и не красивое. Не обязательно даже, чтобы линии совпадали — пример с Apple доказывает, люди видят совпадение там, где его и близко нет.
Можно нарисовать по «Золотому сечению» полный шлак
Есть клиенты, которые уверены, что все великие логотипы, от «Nike» до «Shell» построены по «сечению». Это далеко не так. Хотя прилепить его туда можно, если постараться — см. пункт выше.
Пропорции «Золотого сечения» сами по себе не гарантируют красивый дизайн и, тем более, какое-то подсознательное влияние на аудиторию. Посмотрите, какой «превосходный» дизайн получился бы у Айфона в пропорциях «сечения». Гармония в каждой детали:
Резюме для заказчиков дизайна
1. Нет, в вашем логотипе не обязательно должны быть «золотые пропорции» — есть куча прекрасных симметричных лого и логотипов с другими пропорциями.
2. Нет, логотип «Apple» не построен по «Золотому сечению» — по интернету просто ходит картинка построения логотипа с как попало приляпаной сверху спиралью. Присмотритесь.
3. Нет, секрет успеха фирмы «Apple» не в этом.
4. Да, ваш логотип могут любить и узнавать и без «волшебных пропорций». Наймите хороших дизайнеров и вложитесь в маркетинг — узнаваемость логотипа зависит прежде всего от него.
Золотое сечение
Мелодия, золотое сечение, число Пи и 3,3333
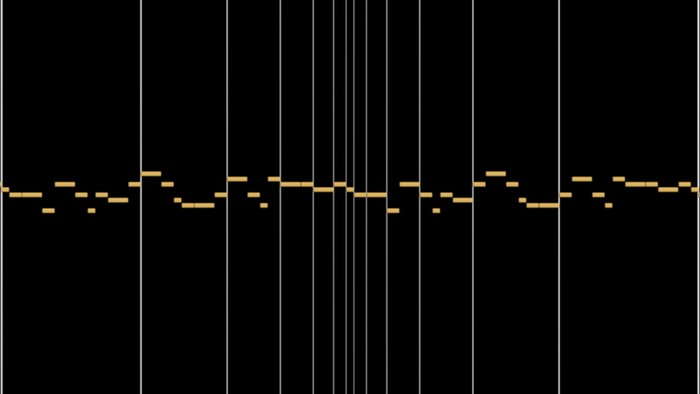
Мелодия имеет интересную особенность: если взять любую пару нот, то длительности этих нот будут между собой в пропорции золотого сечения (Ф=1,61803).
Длительности нот:
a = 1 секунда
b = a / Ф (0,618)
c = b / Ф (0,382)
Таких нот в мелодии 8, 12 и 4.
В сумме длительность мелодии 16,944 секунды.
Если сумму разделить на 4, то получим 4,236. Это золотое сечение в третьей степени. Любые 6 нот мелодии, звучащие друг за другом, в сумме равны Ф в кубе.
Мелодия цикличная, разрешается в первую ноту. Первая и последняя ноты соединяются в пропорции золотого сечения. Длительность мелодии плюс первая нота (a=1) в сумме равны 17,944. Это Ф в шестой степени.
Степени золотого сечения
Первые 2 ноты это Ф. Первые 3 ноты - Ф в квадрате. Первые 6 нот - Ф в кубе. Первые 9 нот - Ф в 4-й степени. Первые 15 нот - Ф в 5-й степени. Первые 25 нот (с учетом цикличности) - Ф в 6-й степени. Первые 41 нота (с учетом цикличности) - Ф в 7-й степени.
Возводить в степень можно и в обратном направлении. Первая и последняя ноты это Ф. Первая и последние 3 ноты – Ф в квадрате. Первая и последние 5 нот – Ф в кубе. Первая и последние 9 нот – Ф в 4-й степени. Первая и последние 15 нот – Ф в 5-й степени. Первая и последние 24 ноты – Ф в 6-й степени. Первая и последние 40 нот – Ф в 7-й степени.
Симметрия
Если взять вторую ноту любого такта, то длительности слева и справа от выбранной ноты будут симметричны друг другу. Тоже самое относится и к пятой ноте.
Если длительность второй ноты последовательно умножать на Ф, то полученные значения будут слева и справа, симметрично выбранной ноты. Точно также и пятая нота (показано на рисунке).
В мелодии есть еще один вид симметрии. Возьмём любую пару нот. Длительности нот, равноудаленные от этой пары, будут между собой в пропорции золотого сечения.
Золотое сечение, число Пи и 3,3333
Если длительность мелодии разделить на 3,3333, то получим 5,0832. Это произведение золотого сечения и числа Пи.
Ролик записан с частотой 30 кадров в секунду. Умножим длительность мелодии на 30 и получим 100 ФП.
Вариант №2
Если взять а = 0,618 (1/Ф) и всё пересчитать, то длительность мелодии составит 10,472 секунды. При делении на 4 будет Ф в квадрате. При делении на 3,3333 будет просто число Пи.