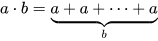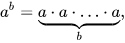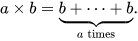Таких примеров с "неправильным ответом" при перестановке множителей - полно. Да: и у меня в начальной школе тоже так было. Я это хорошо помню, потому что с математикой у меня в принципе были большие проблемы, что в школе, что потом в универе.
И я понял, за что снижали оценки, только когда нам стали преподавать педагогику и основы преподавания.
С позиции взрослых людей, у которых за плечами не только школа, но и профильные учебные заведения, многие комментаторы правильно пишут, что от перестановки множителей ничего не поменяется. Получится правильное значение в любом случае. И я с этим тоже согласен.
Но, есть один момент: именно в начальной школе проходят, что такое множимое, что такое множитель. Сначала детей учат понимать, что за результат они получают методом умножения.
Не просто "циферки", а ЧТО конкретно стоит за этими циферками.
А уже потом, в процессе дальнейшего обучения, наоборот, учат именно что абстрагироваться от ненужных условий и "считать циферки".
На первый взгляд, это может показаться нелогичным и даже парадоксальным.
Сначала учат одному и снижают оценки за то, что сделал по-другому. А уже через несколько лет обучения - говорят, что это вообще неважно. Дурость, не правда ли? Некоторые так и заявляют, что, мол, детей учат не думать, а действовать по шаблону и наказывают за "вольнодумство".
Можно сказать, что иногда, к сожалению, бывает и так. Школа "заточена" под среднего ученика. Но, это издержки массового образования, идеала тут достичь не удастся никогда.
При всей кажущейся нелогичности такого подхода, логика там есть. И она в том, что знания даются поэтапно.
Нельзя второклашке объяснять сразу абстрактность математики. Он сразу должен понять смысл простейших операций. Мы сначала понимаем, что делаем, учимся на простейших примерах. А потом, по нарастающей - учимся абстрагироваться от условий. Если второклашке сказать, что это "всего лишь цифры" - то он так и не поймет, для чего все это нужно.
Пример: я в своей работе часто применяю статобработку. Но, основное понимание того, что делаю, я вынес вовсе не из математики в школе или "вышки" (или того же курса статистики) в универе. А из объяснений коллег по работе и из прекрасной книжки "Статистика и котики" В. Савельева. Рекомендую, кстати: отличная книга!
Это результат моих пробелов в знаниях, которые мне пришлось наверстывать уже непосредственно "в поле". Если бы я изначально, в процессе обучения понимал, что делаю (а не просто подставлял циферки в формулы) - было бы гораздо легче.
И так везде. Сначала мы учим простейшие вещи, а уже потом углубляемся в тему. И, оказывается, что то, что мы учили раньше - очень примерно отражает реальное положение вещей. А некоторые данные - вообще неверны (по многим причинам).
Ещё один пример (из биологии): в школе в рамках основ генетики учат рассчитывать цвет глаз потомков на основании цвета глаз родителей.
У одного ребенка голубой цвет глаз, у второго - карий. У матери и отца цвет глаз карий.
1) Определить генотипы детей и родителей.
2) Ответить на вопрос: может ли у двух голубоглазых родителей родиться кареглазый ребенок.
И тут правильным решением определения генотипа будет задача на монозиготное скрещивание А - доминантная аллель (карий цвет), а- рецессивная аллель (голубой цвет) и т. д.
А правильным ответом на второй вопрос будет "нет".
А если начать изучать генетику углубленно, то окажется, что школьная задача - имеет очень отдаленное отношение к реальности.
И составить генотипы родителей по данным условиям невозможно, потому что цвет глаз определяется не парой генов, а сочетанием больше 10 пар генов (из них 2 пары генов - влияют больше всего, остальные - влияют в меньшей степени). И, кроме этого, окончательный оттенок глаз может зависеть не только от генетики и даже меняться в течение жизни, в зависимости от состояния здоровья, гормонального фона.
А ответом на второй вопрос будет: "да". У голубоглазых родителей может родиться кареглазый ребенок.
И вся генетика куда сложнее того, что нам преподают в школе.
Как тут быть? Объяснять все это школьнику, которому такие сложности нафиг не нужны и это не пригодится в жизни? Не объяснять вообще? Или - дать информацию "по верхам". А уже ПОТОМ, если этот школьник поступит в вуз на биологическую специальность, будет изучать генетику углубленно, объяснять, что к чему.
Другое дело, что и учитель тут явно действовал по шаблону. И оценку снижать настолько за решение "не по шаблону" не стоило бы. А ещё лучше - расписать пояснение прямо в тетради.
UPD:
Как и ожидаемо все на пикабу вдруг заделались экспертами по образованию. Лучше учителей и минобразования знают, как надо учить детей.
Да, я сам и писал выше, что в системе образования есть проблемы. Но, описанный мной подход "от простого к сложному" - универсален. Невозможно сразу давать сложный материал.
Что касается множителя, множимого и порядка множителя и множимого. Ссылка, там популярно разжевано, почему именно для второклассников объясняют про важность порядка множимого и множителя:
https://izamorfix.ru/matematika/arifmetika/umnozhenie_natura...
Вот ещё одни подробный разбор этой проблемы: https://dzen.ru/a/X5vfh8CiTCeHWNdw