Искажение спектра в комплексном импульсном пространстве: новый взгляд на неэрмитову физику⁠⁠

Автор: Денис Аветисян

Экспериментальное наблюдение и характеризация искажений спектра в комплексном импульсном пространстве открывает новые возможности для изучения неэрмитовых систем.

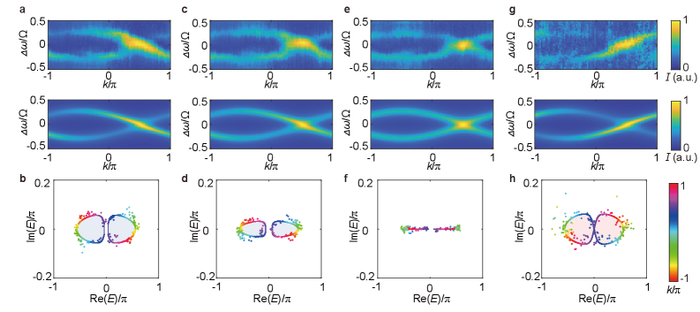
Спектральные измерения, выполненные при значениях μ = 0, -0.1, -0.23 и -0.48 с параметрами (δ1, δ2, η, γ) = (0.31π, 0, 0.25π, 0.057π), демонстрируют соответствие экспериментальных данных теоретическим предсказаниям, подтверждая корректность модели для описания деформации спектра без дальнодействующих связей, при этом точка μGBZ = -0.23, соответствующая границе зоны Бриллюэна, определяет особенности спектра при краевых условиях.

Исследование использует программируемую фотонную платформу для непосредственного изучения не-Блоховской физики и проверки теоретических предсказаний в области топологической теории полос.

Негермотовы системы представляют собой сложный объект для экспериментального изучения, несмотря на предсказания богатого спектра нетривиальных явлений. В работе 'Observation of Non-Hermitian Spectral Deformation in Complex Momentum Space' представлено экспериментальное исследование деформации спектра в комплексном пространстве импульсов, реализованное на основе фотонной решетки с дальнодействующими связями в размерности орбитального углового момента света. Авторы продемонстрировали возможность реконструкции спектральной деформации и прямой регистрации особенностей, таких как исключительные точки и обобщенная зона Бриллюэна. Открывает ли это путь к созданию новых функциональных устройств, основанных на манипулировании негермотовыми состояниями света?

За Пределами Блоха: Новая Эра в Физике

Традиционная зонная теория, основанная на теореме Блоха, неспособна адекватно описывать системы без взаимности или неэрмитовости. Это ограничение актуально для топологических материалов и неэрмитовой оптики, что требует разработки новой теоретической базы. Появление неэрмитовых систем вводит деформацию спектра и неэрмитовский скин-эффект, характеризующийся комплексными собственными значениями и нетрадиционными энергетическими ландшафтами. Отсутствие точного определения задачи обрекает любое решение на шум, и лишь строгая логика может выявить порядок в хаосе комплексных спектров.

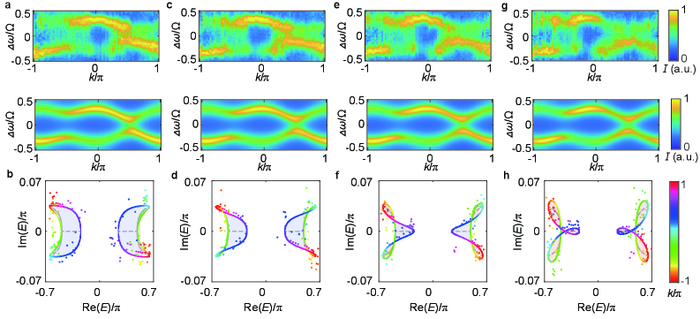
Экспериментальные и теоретические спектры пропускания, полученные при значениях μ = 0, -0.03, -0.06 и -0.09, демонстрируют соответствие между наблюдаемыми данными и расчетами, при этом комплексные собственные энергии, извлеченные из этих спектров (представлены точками), согласуются с теоретическими результатами (сплошными линиями), а спектры собственных значений при граничных условиях Дирихле (обозначены толстыми серыми кривыми) отражают особенности энергетического ландшафта.

Исследование Комплексного Ландшафта Не-Блоховской Физики

Теоретическое описание не-Блоховских зон требует перехода в комплексное пространство импульсов. Это необходимо для корректного учета топологических свойств и их влияния на электронный транспорт. Изучение этого пространства затруднено необходимостью специализированных спектроскопических методов, так как стандартные методы не позволяют адекватно исследовать не-Блоховские состояния. В данной работе используется спектроскопия, разрешенная по комплексному импульсу, для непосредственного отображения спектральных характеристик и подтверждения теоретических предсказаний.

Реализация и Управление Неэрмитовой Физикой с Помощью Света

Для реализации неэрмитовой модели Су-Шриффера-Хегера используется орбитальный угловой момент фотонов, что создает синтетическое измерение для управления свойствами системы. Предложенная платформа обеспечивает контроль спектральных деформаций и наблюдение исключительных точек. Точное управление комплексным импульсом достигается с помощью пространственного модулятора света и фазовой модуляции. Параметры модели SSH устанавливаются значениями расстройки 0.31π, 0, 0.25π и 0.057π для исследования различных конфигураций системы.

Картирование и Характеристика Спектральных Деформаций

Для характеристики спектральных особенностей используется функция Ронкина, описывающая комплексный потенциал. Это позволяет формализовать анализ сложных спектральных распределений. Количественная оценка расстояния между распределениями осуществляется с помощью метрики Вассерштейна, что позволяет сравнивать различные неэрмитовые системы. Полученный ландшафт функции Ронкина, построенный на основе экспериментальных данных и расчетов при параметрах (0.31π, 0, 0.25π, 0.057π), подтверждает соответствие теории и эксперимента. Идентификация обобщенной зоны Бриллюэна (ОЗБ) произведена с использованием самопересечений спектра, значение ОЗБ составило -0.23.

Полученный ландшафт функции Ронкина, построенный на основе экспериментальных данных и теоретических расчетов при параметрах (δ1, δ2, η, γ) = (0.31π, 0, 0.25π, 0.057π), подтверждает соответствие между теорией и экспериментом, что также подтверждается сравнением функции Ронкина при фиксированных значениях E = 0 и E = 0.74π, где экспериментальные данные (точки) согласуются с теоретическими кривыми (сплошными линиями).

За Горизонтом Ограничений: Перспективы Развития

Формулировка Amoeba предоставляет математическую основу для расширения описания не-Блоховских зон на более высокие измерения. Предложенная платформа может быть обобщена для исследования сложных неэрмитовых гамильтонианов и топологических фаз. Исследование неэрмитовых систем открывает возможности для создания устройств с улучшенными характеристиками и изучения новых фундаментальных явлений. Комбинирование спектроскопической техники с новыми материалами и конструкциями позволяет открыть новые функциональные возможности и приложения в фотонике.

Исследование, представленное в статье, демонстрирует элегантную математическую чистоту в изучении деформации спектра в комплексном импульсном пространстве. Авторы, используя программируемую фотонную платформу, не просто наблюдают физическое явление, а подвергают его строгому анализу, подтверждая теоретические предсказания. В этом подходе отчетливо прослеживается стремление к доказуемости, а не просто к эмпирическому успеху. Как заметил Джон Белл: “Игра в физику похожа на игру в шахматы: нужно знать правила”. Действительно, понимание фундаментальных правил негерцовой физики и топологической теории полос является ключевым для интерпретации полученных результатов и построения корректной модели не-Блоховской физики, что и демонстрирует данная работа.

Что Дальше?

Наблюдаемое искажение спектра в комплексном пространстве импульсов, продемонстрированное в данной работе, не является самоцелью, а лишь подтверждением необходимости более строгой математической формулировки физики неэрмитовых систем. Многие существующие модели, хотя и дающие качественное согласие с экспериментом, страдают от недостаточной строгости и не позволяют делать предсказания, свободные от эмпирических параметров. Истинная элегантность заключается в способности предсказать, а не просто описать.

Особый интерес представляет возможность расширения концепции не-Блоховских полос за пределы исследованной области параметров. Существующие теоретические рамки, безусловно, нуждаются в обобщении, чтобы учесть более сложные топологические фазы и взаимодействие с окружением. Необходимо разработать методы, позволяющие предсказывать стабильность и долговечность этих состояний в реальных системах, подверженных шумам и несовершенствам.

В конечном итоге, задача состоит не в том, чтобы найти еще один экзотический эффект, а в том, чтобы выявить фундаментальные принципы, лежащие в основе неэрмитовой физики. Истинное понимание придет лишь тогда, когда математическая модель системы станет неотделима от ее физической реализации – когда алгоритм будет доказуемо корректен, а не просто «работать на тестах».

Оригинал статьи: xpla.ru/iskazhenie-spektra-v-kompleksnom-impulsnom-prostranstve-novyj-vzglyad-na-neermitovu-fiziku

Связаться с автором: linkedin.com/in/avetisyan