Речь пройдет про этот пост, в котором шла речь про построение эллипсов, где нашлось много "экспертов" утверждающих, что всё что я показываю сплошь неправильно и профански
Пример подобных сообщений:
Я человек рефлексивный, остро реагирую на происходящее, и когда увидел подобные сообщения, усомнился в своей точке зрения.. давайте проверим это вместе?)
Я решил начать построение эллипса с плоскости в пространстве.
ЧАСТЬ ПЕРВАЯ
1. Рисуем плоскость
На картинке можете наблюдать линию горизонта( далее ЛГ), висящую в воздухе плоскость, которая имеет точку схода в точку на ЛГ
2. Поиск центра плоскости
Рисуем диагонали из противоположных углов плоскости, в точке пересечения рисуем горизонтальную линию, которая поделит плоскость ровно пополам. Для полноты картины, ведем линию из центра плоскости в точку схода.
Таким образом мы нашли у плоскости 4 точки, которых будет касаться эллипс. Не забываем, что главная наша цель — эллипс.
3. Построение эллипса
Легкими линиями намечаем, как у нас будет проходить линия эллипса.
Хочу обратить ваше внимание на направление движения линии от точки касания эллипса. Линия в самом начале подчиняется направлению стороны плоскости, но затем отрывается от нее.
Точно также и с обратным направлением. Сравните эти две картинки и увидите разницу в форме
4. Обводим жирным ближнюю кромку
В процессе построения, я не оперировал какими-то утверждениями, что "эллипс не имеет перспективного сокращения", а просто рисовал так, как подчиняет рисовать нас форма плоскости, в которую я вписывал с вами в окружность. Но если эллипс разрезать вдоль по самой широкой его части, то можно наблюдать следующую картинку
Мы заметим, что эллипс имеет смещение в направлении "ближе к нам". И по факту его верхняя и нижняя часть будут равны. Т.е центр эллипса не находится на оси его симметрии.
ЧАСТЬ ВТОРАЯ
"И все таки она вертиться!"
Не хватает мне нервов спокойно читать комментарии про то, что у эллипса обязательно должно быть сокращение. Что верхняя часть должна быть больше, чем нижняя часть. Давайте я расскажу, что не учитывают уважаемые "знатоки" в комментариях
1. Касательная к окружности
Именно об этой вещи не знают таки ребята, как @SemiDry и @hokeliver
А еще, уважаемый @SemiDry, я постоянно ошибки допускаю в орфографии, благо хоть @FoxWithoutAName стабильно пишет правки в комментариях
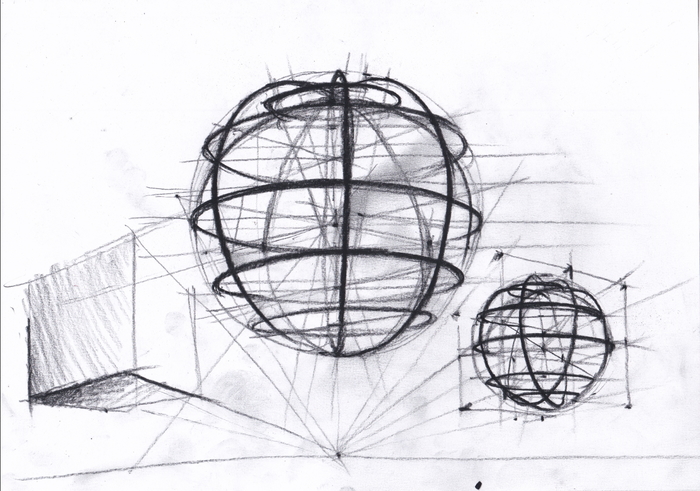
Хоть мы и обладатели бинокулярного зрения, но рисовать приходится только с одной точки зрения. Поэтому, когда перед глазами у нас, к примеру, сфера, то мы видим не 50% ее поверхности, как кажется на первый взгляд, а только лишь 38-40 процентов, в зависимости от того, как близко находится сфера.
На картинка сверху: S - точка зрения, p1 и p2 - точки касания лучей зрения к поверхности окружности.
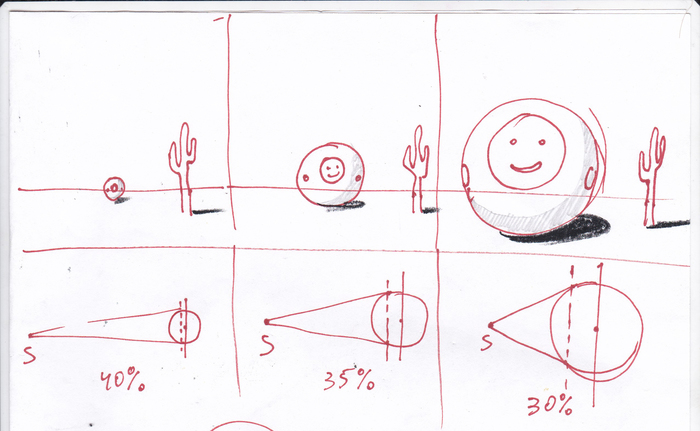
Эту зависимость можно увидеть на картинке ниже. Когда вы моргаете, этот шарик становится ближе к вам. Не моргай. Обратите внимание на размер смайлика на шарике. Чем ближе шарик, тем больший процент от поверхности будет занимать смайлик. На втором кадре еще можно наблюдать его ручки, а на третьем ручки уже почти скрылись за экватор видимости. Такими манипуляциями создают иллюзии приближения в мультипликации.
На картинке снизу, в нижней половине, можно проследить эти зависимости. Чем ближе объект, тем бОльшим углом зрения нужно обладать, чтобы увидеть объект целиком. В первом случае, видимая часть шарика занимает 40% от общей площади. Во втором 35%. В третьем 30%. Если моргнете еще раз, шарик окажется у вас за спиной :3
Пост получился объемным, а на часах 23:40 и завтра еще на работу ;C поэтому я разобью эту тему на две части) В первой части мы приоткрыли тайну эллипса, а во второй я отвечу на вопрос, почему же эта загадочная "касательная к окружности" так портит нам малину и искажает наши с вами эллипсы
Пишите свои комментарии) Буду рад ответить на ваши вопросы) А для тех, кто заинтересовался работой с углом зрения и эффектом приближения рекомендую ознакомится с моим роликом про картинную плоскость