Немного о теории Галуа
Многим французский математик Эварист Галуа запомнился, как мечтатель, погибший в свои двадцать лет на дуэли. И относительно немногие знают, что этот замечательный человек - предтеча современной криптографии.
Криптография (кратко) это наука о том, как найти такое преобразование (отображения множества групп читаемых человеком символов (слов) во множество символов, представляющих в совокупности сумбур (в виде специальным образом исковерканных слов), в идеале (математики, изучающие кольца извините за каламбур) также и подразумевающие, что из этих исковерканных "слов" **однозначно** можно восстановить слова исходные.
Есть такой шифр, называющийся шифром Цезаря. Каждая буква сообщения преобразуется в другую букву, номер которой равен номеру исходной плюс ключ (так сказать, число, однозначно задающее вид отображения, или шифрования), меньший мощности (количества элементов) алфавита: например возьмём для русского алфавита (33 буквы) ключ "1". "а" отображается в "б", "б" в "в", ..., а буква "я" отображается в "а", так в букву "a" может отобразиться только элемент под номером -1, то есть находящийся под номером 32 (если считать с нуля, как это принято в модулярной арифметике).
Однако, данный подход, как и шифр Виженера (хотя и в меньшей степени), подвержен двум критическим огрехам: неустойчивости к крипточастотному анализу и большой (недопустимой для практического применения с XIXвека) длине ключа.
Таблица сопоставления ключу в диапазоне A-Z (или 0-27) подменной буквы
Хороший криптоалгоритм не должен полагаться на неточные (в случае конечности приближений) пределы вещественных чисел, а работать над множествами чисел (полями), где определены знакомые нам (или почти знакомые, так как математики так до конца с ними так и не разобрались (посмотрите для примера abc гипотезу)) операции сложения и умножения, не выводящие при своём применении за рамки этого множества -далее поля.
Монохомное представление таблицы умножения в GF23, любезно предоставленное WolframAlpha
Итак, для простоты представления, будем считать, что поля имеют характеристику (количество своих элементов) равное простому числу (по теореме Лагранжа, по сути говорящей об этом же), хотя есть и поля с характеристикой p^n для любого натурального n, где p- простое число.
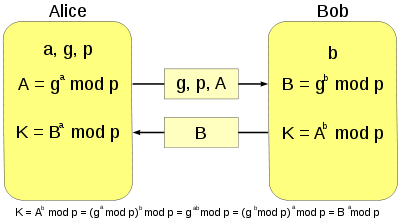
Данный пост лишь показывает верхушку айсберга - поэтому я презентую здесь лишь применение конечных полей в сфере обмена ключей алгоритмом Диффи-Хеллмана, который является ведущим способом реализации, собственно обмена криптографических ключей.
Для дальнейших объяснений я введу понятие взятия остатка от деления a на b: пусть a раскладывается как xb+y, причём x,y могут принимать значения 0. Тогда y называется остатком от деления a на b и записывается y= a mod b. Причём, если a делится на b, то y=0, иначе y<b. Говоря простыми словами - остаток от деления a на b 0- это расстояние от ближайшего числа, меньшего a и кратного b.
Для объяснения, введём трёх персонажей: добрых Алису и Боба, желающих провести беседу инкогнито, и Еву, пытающуюся *роскомнадзор* их переписку.
Итак, алгоритм:
1)Алиса и Боб договариваются о параметрах алгоритма g и p - некоторые натуральные числа, не являющиеся секретом.
2)Алиса и Боб генерируют большие случайные числа - a и b соответственно
3)Алиса вычисляет A=g^a mod p, что является остатком от деления g^a на p
4)Боб аналогичным образом вычисляет B=g^b mod p
5)Алиса и Боб обмениваются числами A и B.
6)На втором этапе Алиса на основе имеющегося у неё a и полученного по сети B вычисляет значение: B^a mod p = g^ab mod p
7)Боб же в свою очередь вычисляет A^b=g^ba mod p
8)Из теорий конечных полей, разработанных Галуа следует, что числа, полученные на шагах 6 и 7 - g^ab и g^ba равны, то есть являются числом, доступным **только** Алисе и Бобу, а Еве, знающей g,p и g^a mod p, g^b mod p необходимо вычислить дискретный логарифм чисел a и b по основанию g соответственно, что для современной математики не является неразрешимой задачей, однако для современных неквантовых компьютеров, являющейся крепким орешком.
Резюме: этот пост не показал всю красоту теории Галуа, но призван показать, что теория конечных полей находит применение на практике. Изложил материал кратко, надеюсь, было не скучно)