Гений Пифагора. Часть 2. Почему в рекурсивно-вычисляемом клеточном автомате Вселенной наше сознание бессмертно?
Продолжение первой части.
Жизнь и математика
Британский физик‑теоретик Стивен Хокинг в своё время много размышлял о природе реальности. В своей книге «Краткая история времени» он задаётся вопросом о том, что будет, если мы откроем физическую «теорию всего»:
Даже если мы откроем полную теорию, это всё равно лишь набор правил и уравнений. Что же «вдыхает огонь» в эти уравнения, чтобы они описывали Вселенную? Почему существует именно та Вселенная, которую они описывают?
Этот вопрос сильно заинтересовал шведского астрофизика Макса Тегмарка. Размышления привели его к написанию книги «Наша математическая Вселенная». Согласно приведённым в этой книге рассуждениям, если выкинуть из наших теорий физики весь словесный описательный багаж, то там не останется ничего кроме формул, описывающих как одни абстрактные математические структуры взаимодействуют с другими. А раз ничего другого, кроме как привести список математических формул, мы о природе реальности сказать не можем, то значит эта самая природа реальности представляет собой чистую математику. Но почему же физический движок Вселенной содержит именно этот набор формул, а не какой‑то другой?
Согласно рассуждениям Тегмарка, в этом нет ничего удивительного, достаточно просто применить к нашей Вселенной принцип Коперника, гласящий, что учёному имеет смысл считать, что место, где мы обитаем, абсолютно заурядно и существует огромное количество подобных ему. Применив этот принцип к своей теории, Тегмарк сделал вывод, что существует бесконечное количество разных математических вселенных, в каждой из которых свой набор базовых математических структур и свой список формул физических законов. В некоторых из этих миров возможно появление жизни, и там, где она появляется и развивается до разумной, существа задаются вопросом о том, почему в их мире именно такой набор физических законов, а не какой‑то другой. Этот аргумент — пример аргументации через антропный принцип.
Если принять картину мира Макса Тегмарка, то можно сказать, что материальные предметы — это не тень вечных и неизменных математических идей, а они и есть эти самые чистые математические идеи. Мир по Тегмарку не делится на идеи и материю, а представляет собой взаимодействие чистых идей.
Задолго до Тегмарка похожие взгляды на мир высказывал американский физик Джон Уилер. Он считал, что в основе мира лежит информация и её обработка, и что основным кирпичиком мироздания служит наименьшая единица информации — бит. Слово «бит» образовано от английского словосочетания «binary digit», что означает двоичная цифра, так как в двоичной системе счисления числа записываются с помощью всего двух цифр 0 и 1. Ноль кодирует отсутствие сигнала, а единица его наличие. Свою философскую теорию Уилер поэтически назвал «it from bit». Можно заметить, что эта идея Уилера сильно напоминает философию Гегеля: ноль — это ничто, единица — это бытие, а их «борьба» порождает мир.
Идеи Тегмарка о математической природе реальности и идеи Уилера о том, что в основе мира лежит информация, развил британский математик и физик Стивен Вольфрам. Его больше всего волновал вопрос о том, почему все физические процессы проистекают в движении и почему присутствует ярко выраженная ассиметрия времени. Почему мы помним прошлое, но не знаем будущее? Почему события в прошлом влияют на события в будущем, но не наоборот? Почему энтропия в термодинамических процессах со временем нарастает? Свои ответы на эти вопросы Вольфрам изложил в книге «Новый вид науки» и статье «Кажется, мы близки к пониманию фундаментальной теории физики, и она прекрасна».
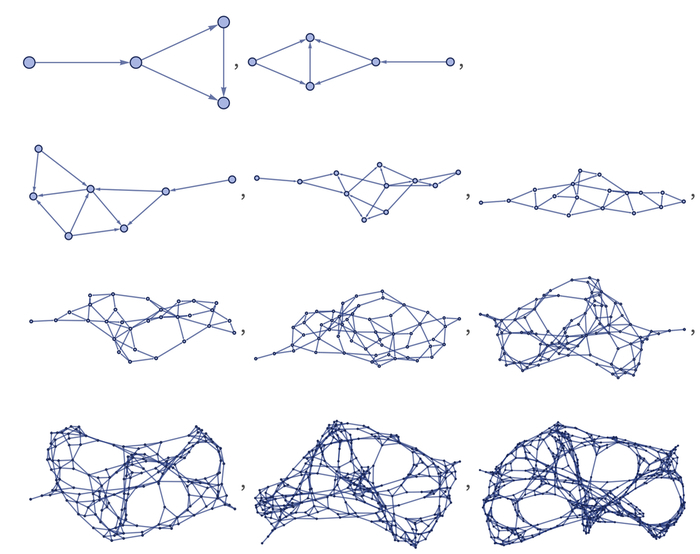
Вольфрам пришёл к выводу, что мир представляет собой не набор статичных математических формул, записанных в её «физический движок», а рекурсивный итеративный вычислительный процесс, который шаг за шагом применяет определённые правила преобразования к некой абстрактной математической структуре, которую можно представить в виде графа. В такой картине реальности формулы физических законов находятся не в основании мира, а выводятся из особенностей изменения этого графа во времени. Ассиметрию времени же учёный объяснил вычислительной необратимостью. Он приводит в пример ассиметричную криптографию: перемножить сотни длинных простых чисел элементарно, а вот с обратным процессом факторизации числа на простые множители не справится даже суперкомпьютер.
Простейшие рекурсивные вычисления могут порождать невероятную сложность и красоту. Так самая прекрасная из известных человечеству структур, множество Мандельброта, вычисляется по простой рекурсивной формуле:
Получающаяся в ходе раскраски попадания или непопадания точки на комплексной плоскости в это множество картина поражает воображение. Пред глазами предстаёт бесконечно глубокий и бесконечно прекрасный фрактал.
Вдохновление для своей теории вычислимой вселенной Стивен Вольфрам почерпнул в изучаемых им всю его жизнь клеточных автоматах. Самый известный клеточный автомат — это, несомненно, игра «Жизнь», придуманная английским математиком Джоном Конвеем. Действие игры «Жизнь» происходит на поле, состоящим из квадратных клеток. Это поле либо бесконечно во всех направлениях, либо замкнуто в само себя. Пустые белые клетки считаются мёртвыми, а закрашенные чёрные — живыми. Раз в ход поле перерассчитывается. В пустой мёртвой клетке, с которой соседствуют три живые клетки, зарождается жизнь. Если у живой клетки есть два или три живых соседа, то эта клетка продолжает жить, если больше или меньше, то она умирает.
Несмотря на столь простые правила, в игре возникают многочисленные виды сложных структур, применение правил игры к которым перемещает эти структуры в соседние клетки. Это создаёт ощущение, что структура движется, и что она — живая. Самый известный пример такого живого организма в игре — это планер, состоящий из пяти живых клеток. Кроме того, в игре могут возникать и более сложные механизмы, которые порождают множество более примитивных. Пример такой структуры — планерное ружьё, исторгающее из себя планеры. Забавный факт: в игре «Жизнь» существуют «сады Эдема» — конфигурации, недостижимые в ходе эволюции клеток, но с которых можно начать игру.
Перемещение планера
Планерное ружьё Госпера
Другим интересным примером клеточного автомата служат самовоспроизводящиеся клеточные автоматы, созданные американским физиком Джоном фон Нейманом. Их особенность состоит в том, что они способны производить свои точные копии рядом с собой. Автоматы фон Неймана сильно напоминают биологические клетки, способные к саморепликации в ходе своего деления.
Универсальный конструктор Фон Неймана
Все эти примеры наводят нас не только на идеи о вычислительной природе Вселенной, но и на параллели между теорией клеточных автоматов, физикой элементарных частиц и теорией эволюции. Вполне возможно, что частицы вроде электрона на базовом уровне представляют собой нечто, похожее по принципам своего перемещения на планеры из игры «Жизнь» и биологические клетки, живущие в воде. Взгляд на Вселенную как клеточный автомат отлично раскрывается в недавней статье «Наша Вселенная — симуляция на основе большого клеточного автомата?».
Теория пыли
Австралийский писатель‑фантаст Грег Иган в своём романе «Город Перестановок» устами одного из персонажей излагает теорию о независимости вычисления сознания от субстрата, на котором оно «запущено». Эта теория в романе именуется «теорией пыли». Но прежде, чем приступить к её описанию, давайте разберёмся с тем, что такое сознание.
Сознание — это субъективный взгляд человека «от первого лица», его точка восприятия мира. Именно в сознании математические сигналы внешнего мира становятся цветами, звуками, запахами, вкусами и чувствами. С философской точки зрения, сознание не может быть причинно редуцировано к работе нашего мозга, но оно полностью коррелирует с изменениями состояния нейронов. Более подробно, философию сознания и все связанные с ним проблемы я раскрываю в эссе «Cознание — величайшая загадка Вселенной», а пока что для наших целей достаточно и этого короткого определения.
Вычисления возможно проводить на разных субстратах: наш мозг проводит свои вычисления с помощью электрохимических процессов в нейронах, в компьютерах вычисления происходят с помощью электрических импульсов в транзисторах, на старых бухгалтерских счётах вычисления происходят с помощью деревянных бусин. Существуют и более экзотические субстраты для вычислений: так китайский писатель‑фантаст Лю Цысинь в своём романе «Задача трёх тел» описывает построение китайским императором и его советниками компьютера, функционирующего на основе солдат с флажками в руках.
Каждый солдат в таком компьютере‑армии симулирует отдельный транзистор и знает только, должен ли он поднять флажок или нет, если флажок поднял соседний с ним солдат. Небольшой отряд представляет собой логический вентиль «И», «ИЛИ» или «НЕ». Из этих отрядов строятся батальоны процессора и полки оперативной памяти. Дебаггинг император в романе проводит интереснейшим способом: после проведения массовых казней в забагованном элементе системы соседние элементы понимают намёк и начинают функционировать правильно. Отдельный солдат в таком компьютере не знает, какие вычисления проводит вся армия целиком. Точно так же отдельный транзистор не знает, что вычисляет компьютер, а отдельный нейрон не знает, о чём думает мозг.
Многие современные философы придерживаются мнения, что сознание сопровождает любые сложные процессы обработки информации, а, значит, его можно запустить хоть на компьютере, хоть на китайском компьютере‑армии Лю Цысиня. То есть, достаточно сложные искусственные нейронные сети тоже могут обладать сознанием. Верность этой гипотезы позволит загружать сознание в компьютер при смерти биологического тела человека. Именно из рассуждений о загруженном в компьютер сознании Грег Иган и выводит свою теорию пыли. Писатель предлагает следующий мысленный эксперимент.
В эксперименте участвуют двое: существующий во «внешнем» мире экспериментатор‑программист Алиса и существующий в виртуальной реальности экспериментируемый — Боб, чей мозг и окружающий его мир полностью симулируются в запущенной на компьютере Алисы программе. Алиса просит Боба вслух сосчитать от одного до десяти. Тот считает: раз, два, три, четыре, пять, шесть, семь, восемь, девять, десять. Во время счёта Алиса несколько раз нажимает то на кнопку паузы, то на кнопку продолжения симуляции. Для неё счёт Боба, доносящийся из колонок звучит так: раз, два, долгая пауза, три, четыре, пять, долгая пауза, шесть, семь и так далее. Для Боба же это просто непрерывный счёт — он не ощущает пауз, так как в моменты паузы он просто не вычисляется.
Из этого Иган делает вывод, что в этом случае мы наблюдаем две субъективных вселенных — одну Алисы и одну Боба, которые как‑то связаны между собой, но в которых время течёт совершенно по разному. Можно сделать так, что пока Боб будет считать от одного до десяти, во вселенной Алисы пройдут десятки лет. Это чем‑то напоминает эффекты замедления времени в теории относительности. Но это не главное. Дальше Иган делает ещё более интересный шаг в рассуждениях.
Что будет, если поставить Вселенную Боба на паузу, а после перенести симуляцию на другой компьютер и запустить там? Боб ничего не заметит. Что будет, если поставить Вселенную Боба на паузу, после перенести симуляцию на компьютер в виде китайской армии Лю Цысиня, вычислить ещё пару шагов там, опять поставить на паузу, а спустя год перенести обратно? Боб ничего не заметит. Для него счёт вслух будет непрерывен. И тут Иган наконец‑то подходит к своей теории пыли.
Если сознание как вычислительный процесс не зависит от субстрата, на котором оно вычисляется, и если оно течёт непрерывно даже, если моменты его вычисления разделены десятками лет, то почему состояние сознания последующее за тем, которое сейчас закодировано в структуре моего мозга, не может быть закодировано в структуре облака космической пыли в далёкой галактике?
Подобный вопрос до Игана задавали себе и другие мыслители. Например, известна концепция под названием «Мозг Больцмана», согласно которой случайные флуктуации вакуума могут приводить к возникновению в космосе структуры подобной мозгу, у которого будет память о всей его прошлой жизни и представления о некой Вселенной, в которой он обитает.
Персонаж Игана после открытия «теории пыли» строит компьютерную симуляцию под названием «Город перестановок» — клеточный автомат, чьи правила позволяют бесконечный рост вычислительных мощностей. Этакий программистский рай. Персонаж заселяет в этот новый дивный мир свою копию и отключает компьютер. Вселенная, в которой живёт его копия, продолжает своё субъективное существование дальше...
Вселенная как число
Концепции математической вселенной Тегмарка, информационной вселенной Уилера, вычислимой Вселенной Вольфрама и теорию пыли Игана развивает в своей работе «Вселенная как число» российский программист Илья Шепрут. В этой работе каждое конкретное состояние Вселенной соотносится с определённым натуральным числом. Таким образом, история Вселенной представляет из себя просто ряд натуральных чисел.
Существует бесконечное количество таких возможных рядов. Есть вселенная, где после состояния 1 идёт состояние 2, есть вселенная, где после него состояния 1 идёт состояние 3, и так далее. Это роднит концепцию Шепрута с многомировой интерпретацией квантовой механики Хью Эверетта, согласно которой в разных мирах одновременно существуют все возможные исходы «случайных» квантовых событий, и каждый из таких миров имеет свою историю.
Эти ряды натуральных чисел, кодирующие разные истории Вселенной, подобны поэтическому описанию сада расходящихся тропок у аргентинского писателя Луиса Хорхе Борхеса. В его одноимённом рассказе описан вымышленный сад, в котором тропинки символизируют различные варианты истории одного и того же человека. Каждое принятое человеком решение образует развилку, от которой независимо друг от друга идут две другие тропинки, или сливаясь в будущем обратно или же никогда более не пересекаясь.
При этом, согласно теории Шепрута, не имеет никакого смысла говорить о том, живём мы в Матрице или нет, является ли наш мир симуляцией или нет. Существует бесконечное количество историй, в которых наша вселенная — это симуляция внутри других вселенных, и бесконечно количество историй, где наша вселенная — это независимая реальность.
Интересный вывод из теории пыли Игана и концепции «Вселенная как число» Шепрута заключается в том, что Сократ и Платон были не так уж далеки от истины, когда говорили о бессмертии души. Ведь состояние нашего сознания, согласно этим теориям, тоже может быть закодировано в виде числа, и существует бесконечное количество историй с последующими от текущего состояниями. Это делает нас субъективно бессмертными.
Это чем‑то напоминает мысленный эксперимент с квантовым бессмертием, придуманный физиками Хансом Моравеком и Бруно Маршаллом. Суть эксперимента такова: создается устройство — ружьё, чей спусковой крючок привязан к детектору распада неких радиоактивных атомов. Если атом распадается, автомат стреляет, если нет, то просто щелкает. Вероятность выстрела зависит от коллапса волновой функции при распаде атома и равна 50%. Процесс измерения распада атома происходит раз в секунду, то есть раз в секунду автомат либо стреляет, либо просто щёлкает.
Если мы смотрим на этот автомат со стороны, то мы слышим и видим абсолютно случайную последовательность выстрелов и щелчков: выстрел, щелчок, выстрел, выстрел, щелчок, выстрел, щелчок, щелчок, выстрел, щелчок. Но как только мы помещаем нашу голову на линию огня автомата происходит магия — автомат только щёлкает и никогда не стреляет. Как такое возможно?
Всё дело в том, что в тех параллельных вселенных, где автомат выстрелил, вы умерли, а остались в живых вы только в той единственной вселенной, где автомат всегда щёлкал. Поэтому не стоит показывать этот эксперимент вашим друзьям: за минуту стояния на линии огня квантового автомата в 60 параллельных вселенных ваши друзья увидят как ваши мозги разлетаются по стене, и лишь в одной из них вы сможете сказать им: «Вот видите, я же говорил, что я бессмертный». В такую версию бессмертия в конце своей жизни в нашей вселенной верил сам создатель многомировой интерпретации квантовой механики Хью Эверетт.
Если существует бесконечное количество возможных продолжений, то наше «внутреннее кино», как называет сознание австралийский философ Дэвид Чалмерс, никогда не подойдёт к концу. Процитирую отрывок об этом из оригинальной статьи Ильи Шепрута:
Я даже могу предложить вам множество примеров вселенных, которые возможно сконструировать, в которых вы можете ощутить себя после смерти:
Оригинальная вселенная, но вы просыпаетесь в психушке, и вам говорят, что вы не умирали.
На случайной пустынной планете с фиолетовым небом и равномерным освещением, как будто во время дождя. Далее вы умираете от голода и жажды.
В симуляции, где всех людей возродили одновременно и предоставили им бесконечные вычислительные ресурсы для симуляции самих себя, а ваш мозг был получен сверх‑ИИ, который был создан человечеством, чтобы этот ИИ смог получить состояние всех частиц нашей вселенной и просимулировать её назад, чтобы воскресить всех живых существ и предоставить им программистский рай.
В 12-мерном пространстве, и вы являетесь суперсуществом, которое только что сыграло в игру «почувствуй себя человеком, максимальное погружение». Для этой вселенной симуляция нашей является лишь игрушкой. И вам кажется мелочью вся эта человеческая жизнь и её печали, и вы возвращаетесь к своим 12-мерным делам в супервселенной.
Аналогично прошлому пункту, но это всё было сном.В квадратной комнате, при этом вы не чувствуете голода или жажды, и не можете себя убить, и вам там абсолютно нечего делать навечно.
Вас сделали бессмертным и стали бесконечно пытать всеми возможными способами без возможности выбраться или умереть.
В раю с 72 девственницами.
Вы оказались в центре Солнца. Умерли. Посреди пустого космоса. Умерли. В 60-мерном пространстве. Умерли. В 2-мерном пространстве. Умерли. Внутри компьютерной игры. Не умерли.
Как видите, возможные варианты разнятся от крайне приятных и интересных, нейтральных и занимательных до вселенных с бесконечными страданиями. И именно вселенные со страданиями мне и не нравятся, я бы хотел как‑то запретить их существование, но такое не подвластно даже Богу. Очень жаль понимать, что некоторым версиям меня придётся это испытать.
Чем это не перерождение душ, в которое верили Пифагор и Будда? Согласно буддизму, существует бесконечное количество райских и адских миров, в которых может переродиться наше сознание, и куда оно попадёт зависит только от нашей кармы...
P.S.: Больше интересных постов и видео про философию, буддизм и математику вы можете найти в моём телеграм-канале.