Привет! Большинство считает, что комплексные числа вылезли к нам из астральных планов бытия, что мнимая единица - это глашатай нечеловеческого разума, что эти чуждые рассудку существа гнездятся где-то внутри нашего с вами существования, что они образуют большой палец... Я курил на балконе и понял, что хочу пройти в самые уголки нашего существования, чтобы утереть нос всем словоблудам-философам, ибо овладев комплексными числами, я специально для них выстрою комплексный средний палец. А поскольку мне страшно проникать в такие леса, я беру с собой вас, рабочих и крестьян Пикабу. Ну, кто смелый?! Кто со мной! Раз-два, шагооом марш.

Приготовления к спуску

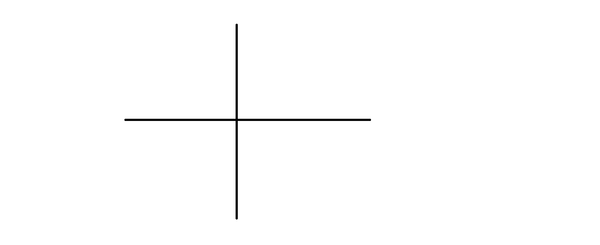
Те солдаты, которых не отпугнуло моё введение и которые, соответственно, пошли со мной, я обращаюсь именно к вам. Трусов к чёрту, как говорится. Итак, тоrищи, нам нужна экипировка. Фонарик? Какой фонарик?! Уберите его. Возьмём две палки и мел. Нет-нет, мы не будем устраивать махач, здесь же нет философов, чтобы устраивать разрешение всех философских вопросов, нет. Просто дело в том, что для попадания в астрал нам нужно провести обряд. Отцы-оккультисты-террористы-мазохисты-нигилисты-идеалисты написали в своей Тайной Книге (с названием "Общая алгебра"), что обряд заключается в песнопениях, бубнах и плясках символе креста и некоторых меловых доработок до Креста Действительной Плоскости. Чуете, ветер подул? Это из-за эпичности названия. Итак, встаньте в круг, я кладу палки крестом.

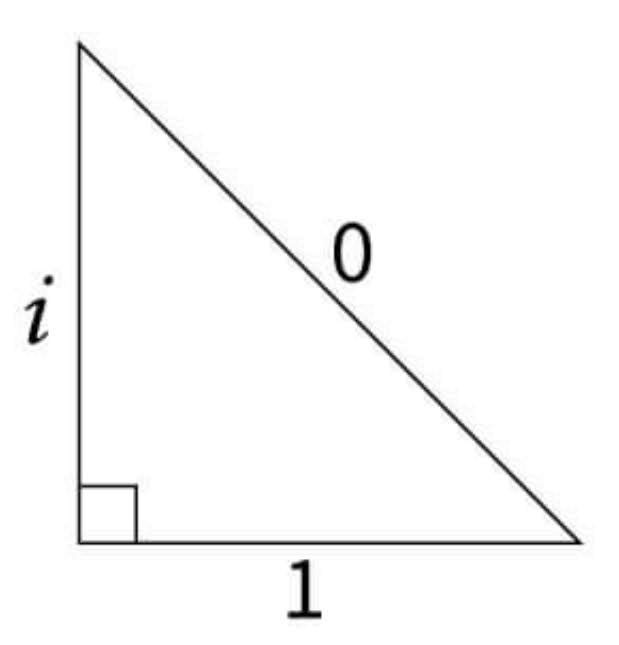
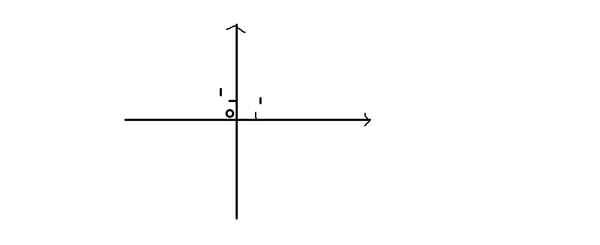
Теперь, согласно Тайной Книге, нам нужно выбрать положительное направление у двух прямых. Я предлагаю сделать положительным направление вверх и вправо, ибо круто. Также нам нужно отметить Центр Мира, точку О, которая является точкой пересечения прямых. И... и прочертить Шаг Дракона в единицу. Ну-ка, делай.

Первая локация: евклидова плоскость

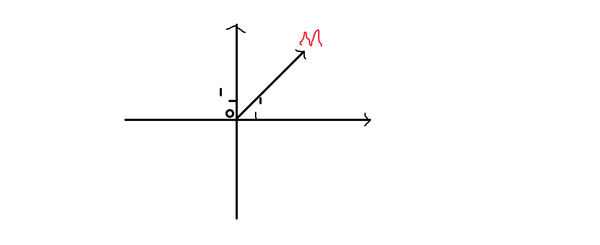
Ух! От неё исходит ветер и сияние! Чтобы мы окончательно попали в иной план бытия, нужно прочитать заклинание по подчинению пространства, которое называется Аксиомами Евклида. Ну-ка, читай. *Чух, чух, чух, чух, ай, нихрена не зашло*. Оно открылось, идём!. Итак, мы, согласно Второй Книге ("Линейная алгебра"), попали в Евклидово Пространство. Боже мой! Мы уже на первом этапе поиска самих пластов существования - Комплексной Плоскости! Так, давайте здесь осмотримся. Каждая ось (прямая со стрелкой) суть упорядоченное множество действительных чисел, то есть все числа в их порядке. Если мы будем скользить по правой оси, которую назовём Ox, по стрелке, то будем видеть числа -1, -0.98, -0.97... Чем больше число, тем оно правее, поэтому оно упорядочено. Это так называемая одна из реализаций множества R, то есть множества действительных чисел. Абсолютно аналогичная ситуация с осью Oy, которая верхняя, да. Что же тогда такое белое место вне осей? Что там? Там находится бесконечное количество точек, но наши оси позволяют нам однозначно ориентироваться в них. Почему? Очень просто. Выбираем любую точку M (на прямой или вне) и опускаем из неё перпендикуляры на оси, благо аксиомы евклидовой геометрии на плоскости позволяют. Тогда перпендикуляры пересекут оси в некоторых числах a и b, где a и b принадлежат множеству R. Очевидно, эти два числа однозначно определяют точку, поэтому иногда говорят, что пара (a; b) и есть эта точка, суть синоним. Пишут M(a; b). В такой записи первая ячейка (в которой a) ответственно за число, полученное при пересечении оси Ox. Вторая - Oy. Каждой точке можно совершенно однозначно поставить в соответствие вектор, выходящий из начала координат, и называемый радиус-вектором.

Числа (a; b) называются декартовыми координатами. Мы можем заметить, что любую точку также можно однозначно определить через длину радиус-вектора и угол между ним и осью Ox. Тогда мы получим пару (r; f), где f - угол. Это тоже координаты точки, но уже полярные. Легко от них перейти к декартовым:
a = rcosf

b = rsinf

Что ещё... Ах да, преобразования плоскости. Да, прошу вас также кое-что учесть: мы рассматриваем простую плоскость, которую изучают в курсе планиметрии, просто мы ввели удобный регистр. Никуда в иное измерение мы не ушли (пока, хе-хе). Да, кстати, этот регистр можно представить как робота: мы подходим и спрашиваем, где точка M, а он говорит, что в (a; b). И мы уже знаем, куда нам идти, скажем, a = 3 шага вправо и b = 4 шага вверх. Всё. Теперь отвлекаемся от робота и рассматриваем простую плоскость. Пусть мы сидим в центре мира, а весь мир крутится вокруг нас. Тогда какая-то точка переходит в другую точку. Представьте колесо и зафиксируйте на нём маркером точку. Закрепите также строго вертикальную ось. Теперь включим регистр, который говорит о положении через пару чисел. Тогда эта точка постоянно будет его менять относительно центра колеса, не так ли? Вот она была в (a; b), а теперь она в (c; d). Такой перевод одной точки в другую называют отображением плоскости в себя (сейчас говорим лишь про одну плоскость). Это отображение обозначается через любую букву как функция. Скажем, запись f(A) = B означает, что точка A перешла в точку B при каком-то отображение. B называется образом A при отображении f. Выделяют много типов хороших отображений, рассмотрим некоторые из них. Замечу лишь, что мы будем рассматривать отображение НА себя, то есть преобразование плоскости. Это означает, что оно относится к каждой точке плоскости.

1. Параллельный перенос.

Представим плоскость и отметим на ней одну точку M, зафиксируем некоторое положение (a; b) (мы ввели систему координат). И как бы руками передвинем всю плоскость выше, тогда точка M окажется в этом положении. Если её координаты были M(c; d), то она проделает путь

Ox: l = a - c

Oy: l = b - d

И так каждая точка плоскости, ведь это преобразование.

Иными словами, любая точка с координатами (x; y) (произвольными) переходит в точку (x + a; y + b), где a и b - действительные числа.

2. Гомотетия.

Это такое преобразование, которое переводит точку с координатами (x; y) в точку с координатами (kx; ky), то есть "растягивает", k - элемент R.

3. Поворот.

Вспомните пример с колесом.

Так, солдаты. Зачем нам это было нужно? С этим...

(Продолжение будет, если зайдёт, да).