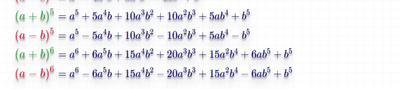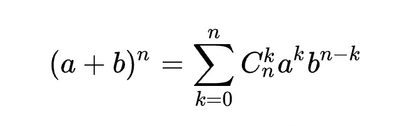Пацаны, у нас тут живая девушка!
вечер перестает быть томным!
ну рассказывайте... и как вам?
Хороший ролик.
Тут есть и про решение кубических уравнений 3-ей степени с помощью геометрии, затронутое ТС

Мне понравилось как рассчитывается масса четырехмерных объектов в трехмерном пространстве, по логике в черную дыру не скалапсирует, но продавит любую материю словно ее нет.
не, смотри
об это очень доходчиво рассказывал Тайсон который не Майк
для ЛЛ:
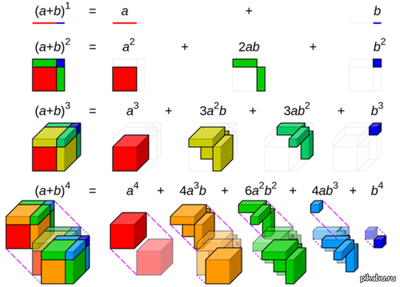
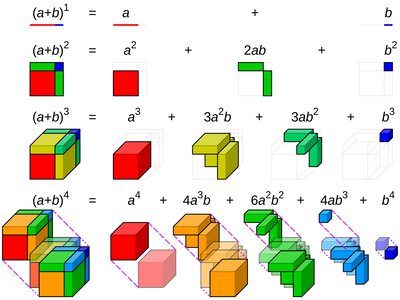
следи как увеличивается размерность пространства.
Есть нульмерная точка, у нее нет никаких измерений
Дальше посмотрим на отрезок -- это одномерная фигура, ограниченная двумя нульмерными точками
Теперь берем квадрат. Двухмерная фигура, ограниченная уже четырьмя фигурами измерения N-1 (одномерными отрезками).
Куб -- трехмерная фигура, "состоящая" из уже шести двухмерных квадратов.
Тогда, фигура следующей размерности будет содержать уже восемь фигур измерения N-1 (то есть кубов)

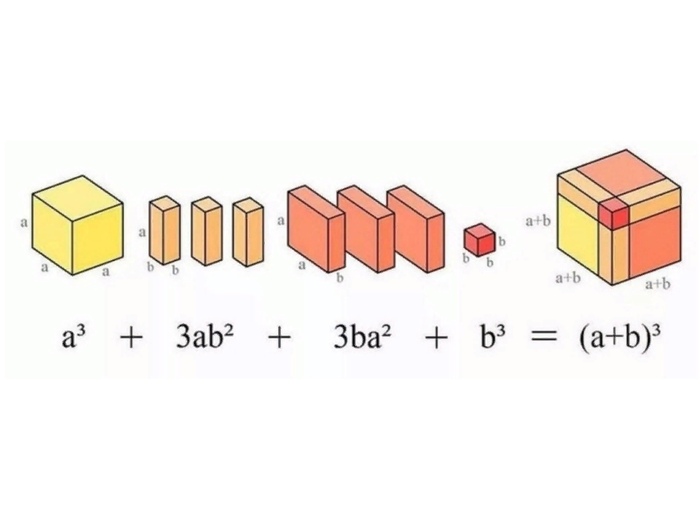
Если b=2а, тогда
(а+b)^1 = 3a - линия т.е.
(а+b)^2 = 9a^2 - 9 квадратиков
(а+b)^3 = 27а^3 - 27 кубиков
(a+b)^4 = 81a^4 - 81 тессеракт
Василий Иванович возвращается из Москвы: где поступал в Академию. Петька спрашивает:
— Василий Иванович, поступил?
— Нет, Петька, на математике завалили! Дают лист бумаги и говорят: «Изобразите квадратный трехчлен». А я не то чтобы нарисовать, а даже представить себе такую гадость не могу...
Ладно, убедили, но на первый вопрос Yandex.Alice мог бы нормально ответить, раз уж рисовал картинку.
Если сделать А и В понятно одинаковыми, нихера не получитсяЭтот неловкий момент, когда элементарную математическую формулу красиво и просто доказали графически, но кто-то всё равно не понял.
Тебя бесит чертёжный шрифт по ГОСТ 2.304?
Соболезную, если тебе придётся работать с конструкторской документацией...
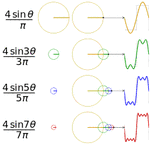
Только это обратное преобразование Фурье.
Прямое это как раз по исходному сигналу найти амплитуды составляющих синусоид (спектр).
Вообще на гифке отображены гармоники меандра. Обратите внимание, что все они нечетные. Чётных у меандра нету.
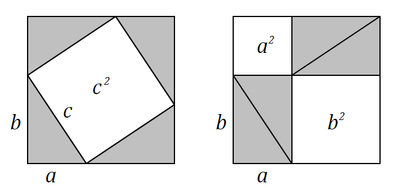
Серьезно? Учебник Атанасян 7-9 класс страница 130 рисунок 186.
Это всем рассказывают, просто ни кто не слушает это в 8 классе
А какого года учебник? В геометрии у нас точно такого не было. Куб суммы шел в алгебре, просто премножали три раза выражение в скобках и сокращали. Я тоже сейчас долго смотрел на картинку, прикольная.
upd Всё. Увидел коммент - с 88 года. Не было у меня такого учебника.
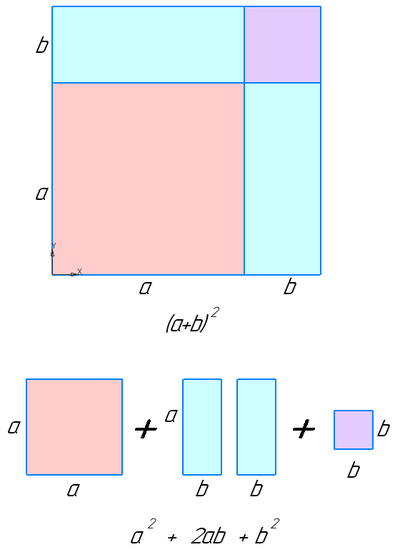
Есть в учебнике алгебры наглядное представление квадрата суммы и разности квадратов, куб суммы сейчас больше рассматривается через треугольник паскаля
Какой учебник к нас был тоже не помню, 30 лет прошло
У меня учебник в 8 классе уже был на латышском, а там эти коммунистические картинки выдраны как кровавое наследие угнетающее латышскую нацию. Зачем нам математика, еще научились бы считать и начали спрашивать кто деньги из бюджета ворует
Есть ещё более мощная визуализация, которую увидел в ролике numberphile с Андреем Окуньковым. Всё можно представить как замощение плоскости 2 видаси квадратов, и на точках получить замощение квадратом 3 вида. Можно бесконечно смотреть:) Там задача про другое, но он ссылается на теорему Пифагора между делом:)

Очень интересным фактом является то, что началом истории математики была как раз таки геометрия. Когда люди не знали цифр, они использовали рисунки и со времени эти рисунки превратились в цифры. Так мы получили современную математику
Я подобную штуку в 8 классе собирал из картона на один из уроков геометрии. Шарниры были, цвета разные, все дела
Мне ещё безумно нравится классическое доказательство, через приведение площади "косоугольных" треугольников к прямоугольным. Неочевидное, но красивое.