0 просмотренных постов скрыто
Сферический мыш в вакууме
Показать полностью
1
День знаний в офисе
Спросил сегодня могут ли коллеги найти цент окружности используя только линейку. Взяли значит первый попавшийся лист, долго думаем всем отделом, рисуем… Потом мне стало интересно, что на обратной стороне листа. Переворачиваю а там заметки по Time Management ) Смеялись долго
Ответ на пост «Коты приятной наружности и во-от такой окружности»1
Мне, пожалуйста, два кофе с муррршмеллоу
Коты приятной наружности и во-от такой окружности1
Показать полностью
1
Геометрический вопрос
Сегодня столкнулся с такой задачей : есть уравнения трёх окружностей и нужно переделить точки их пересечения в общем виде , у кого есть идеи ?)
Окружность и круг | Математика
В этом видео поговорим об окружности и круге, рассмотрим, чем они отличаются друг от друга, а затем выясним, как вычислить градусную меру дуги и длину окружности.
Луночки Гиппократа
Продолжая серию постов о геометрии, захотелось также написать об еще одном великом геометре античности - Гиппократе Хиосском. Несколько его книг Эвклид включил в свои знаменитые "Начала", которые стали основой математики и геометрии для последующих ученых на протяжении двух тысяч лет (в них даже содержится основа математического анализа). Как и многие другие геометры, Гиппократ занимался поиском квадратуры круга, но, в отличие от других философов, пришел в своих исследованиях к интересному открытию - "луночки" - площадь пересечения двух окружностей - квадрируются, то есть с помощью циркуля и линейки можно построить квадрат, площадь которого будет равна площади луночки. Изучая геометрию последние несколько недель, я также изучал геометрические фигуры в природе - аналогом луночки Гиппократа в природе можно считать лунный месяц, который мы часто наблюдаем на небе. Вот несколько примеров нахождения квадратуры луночек:
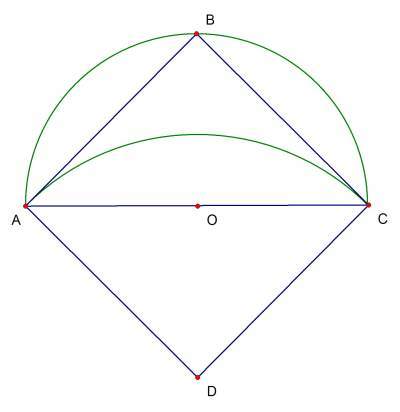
Одну из луночек можно построить следующим образом: возьмем четверть круга и на хорде АС, соединяющей концы радиусов ОА и ОС, опишем как на диаметре внешнюю по отношению к четверти круга полуокружность.
Легко показывается, что площадь луночки равна площади треугольника АВС. Таким образом, луночка квадрируема.
Другая интерпретация этой же задачи на следующем рисунке:
Гиппократ заметил, что суммарная площадь зеленых луночек равна площади квадрата, окрашенного здесь в красный цвет. Действительно, сумма площадей полукругов, построенных на сторонах этого квадрата, равна площади круга, в который вписан квадрат. Если из полукругов удалить окрашенные в черный цвет сегменты, то останутся четыре луночки; если же удалить их из большого круга, то останется квадрат.
Гиппократ получил три квадрируемые луночки. Д. Бернулли в “Математических упражнениях” указал условие, которому должны удовлетворять алгебраически квадрируемые луночки, и привел уравнение, дающее четвертую квадрируемую луночку.
Однако луночки Гиппократа задачу о квадратуре круга вперед к решению не продвинули: в 30—40-х годах XX в. И. Г. Чеботаревым и А. В. Дородновым доказано, что существует пять видов квадрируемых луночек, но они не квадрируемы вместе с кругом.
Следующее предложение доказано арабом Ибн Альхаитамом, а французские математики А. де Лион и Г. Парди высказали его вновь в 1654 и в 1671 г.
Построим на гипотенузе прямоугольного треугольника как на диаметре полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, а на катетах, как на диаметрах, построим полуокружности во внешнюю от треугольника сторону.
Тогда сумма площадей двух получившихся луночек равна площади треугольника АВС.
Здесь интересен еще и следующий факт - луночки являются равноширинными. Диаметры наибольших вписанных в них окружностей равны одной и той же величине, а именно половине разности между суммой катетов и гипотенузой треугольника.
Вот еще один интересный факт, являющийся частным случаем задачи о трех арбелонах. На сторонах прямоугольного теугольника, как на диаметрах, построены три окружности. Они образуют две луночки (выделены оранжевым) и арбелон (выделен серым), а также дуговой двуугольник, обозначенный буквой Т.
Оказывается, что сумма площадей луночек и арбелона без площади криволинейного двуугольника Т равна удвоенной площади треугольника АВС.
Следующий рисунок иллюстрирует еще одну теорему Гиппократа.
Пусть нижнее основание трапеции является диаметром описанной около нее окружности, АВ=ВС=CD и на боковых сторонах и верхнем основании, как на диаметрах построены полуокружности. При этом образуются три равные луночки (выделены серым). Оказывается, площадь трапеции равна сумме площадей этих луночек и полукруга (полукруг равен тем полукругам, из которых образованы луночки).
Показать полностью
6